Un peu de python.
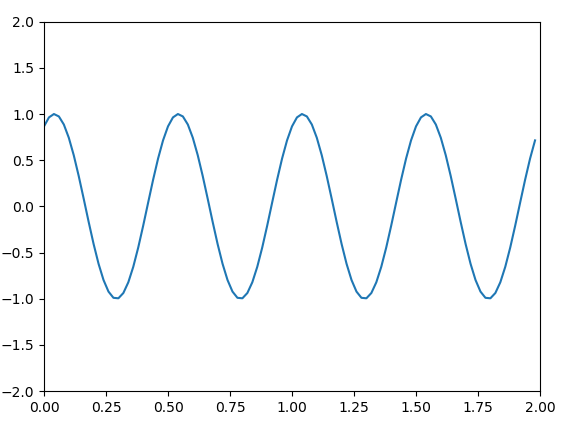
Une courbe
%%%%%%%%%%%%%%%%%%%% %ENSCR 20210928 %une courbe # -*- coding: utf-8 -*- # 202109 # une ligne qui commence par un dièse est une ligne de commentaire # elle n'est pas exécutée par le programme # on importe des bibliothèques, des fonctions from math import sin, pi # pour pouvoir tracer des courbes, on a besoin de 'pyplot' dans la librairire 'matplotlib' from matplotlib import pyplot # temps maximal d'affichage # écrire 2.0 avec le point définit un nombre flottant (float) # écrire 2 définit un entier (int) # pour voir la différence essayer de calculer 1/2 et 1/2.0 ou 1/2. avec le point Tmax=2.0 # on définit les axes (x,y), auxquels on rajoutera les courbes ax = pyplot.axes(xlim=(0, Tmax), ylim=(-2, 2)) # nombre d'échantillons NbEchantillons=100 # on définit les instants de calcul de la courbe temps=[i*Tmax/NbEchantillons for i in range(NbEchantillons)] #TEST: print(temps) # période T=0.5 # courbe macourbe=[sin(2*pi*t/T+pi/3) for t in temps] #TEST: print(macourbe) # on rajoute la courbe sur le graphique ax.plot(temps,macourbe) # on demande l'affichage pyplot.show() |
 |
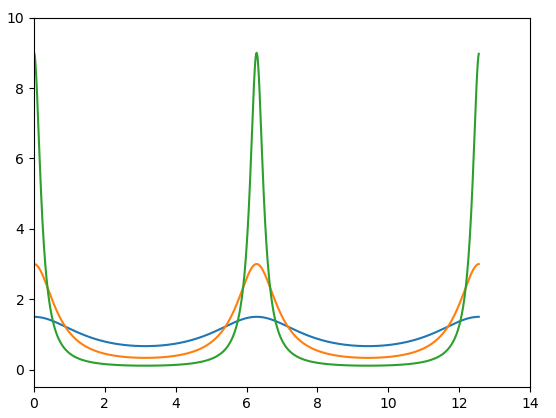
Trois courbes
%%%%%%%%%%%%%%%%%%%%
%ENSCR 20210928
%trois courbes
# -*- coding: utf-8 -*-
# 202109
# une ligne qui commence par un dièse est une ligne de commentaire
# elle n'est pas exécutée par le programme
# on importe des bibliothèques, des fonctions
from math import cos, pi
# pour pouvoir tracer des courbes, on a besoin de 'pyplot' dans la librairire 'matplotlib'
from matplotlib import pyplot
# phase maximale
Phimax=4*pi
# on définit les axes (x,y), auxquels on rajoutera les courbes
ax = pyplot.axes(xlim=(0, 14), ylim=(-0.5, 10))
# nombre d'échantillons
NbEchantillons=1000
# on definit les instants de calcul de la courbe
phases=[i*Phimax/NbEchantillons for i in range(NbEchantillons)]
# pour tracer plusieurs fois la courbe en changeant un paramètre sans tout retaper,
# on définit une fonction
def intensite(R,phi):
return (1-R**2)/(1+R**2-2*R*cos(phi))
# courbe
macourbe=[intensite(0.2,phi) for phi in phases]
macourbe2=[intensite(0.5,phi) for phi in phases]
macourbe3=[intensite(0.8,phi) for phi in phases]
# on rajoute la courbe sur le graphique
ax.plot(phases,macourbe,phases,macourbe2,phases,macourbe3)
# on demande l'affichage
pyplot.show()
|
 |
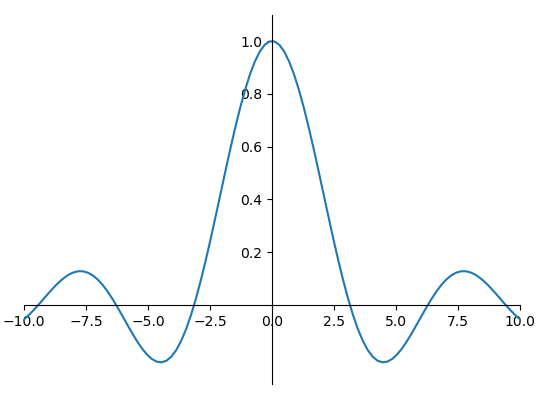
Un sinus-cardinal
%%%%%%%%%%%%%%%%%%%% %ENSCR 20220907 % sinus cardinal # -*- coding: utf-8 -*- # 202209 # on importe des bibliothèques, des fonctions from math import sin, pi # pour pouvoir tracer des courbes, on a besoin de 'pyplot' dans la librairire 'matplotlib' from matplotlib import pyplot # temps maximal d'affichage # écrire 2.0 avec le point définit un nombre flottant (float) # écrire 2 définit un entier (int) # pour voir la différence essayer de calculer 1/2 et 1/2.0 ou 1/2. avec le point Xmin=-10.0 Xmax=10.0 # on définit les axes (x,y), auxquels on rajoutera les courbes ax = pyplot.axes(xlim=(Xmin, Xmax), ylim=(-0.3, 1.1)) # nombre d'échantillons NbEchantillons=101 # on définit les instants de calcul de la courbe abscisses=[Xmin+(Xmax-Xmin)*i/NbEchantillons for i in range(NbEchantillons+1)] #TEST: print(temps) # courbe macourbe=[sin(x)/x for x in abscisses] #TEST: print(macourbe) # on rajoute la courbe sur le graphique ax.plot(abscisses,macourbe) # on demande l'affichage pyplot.show() |
 |
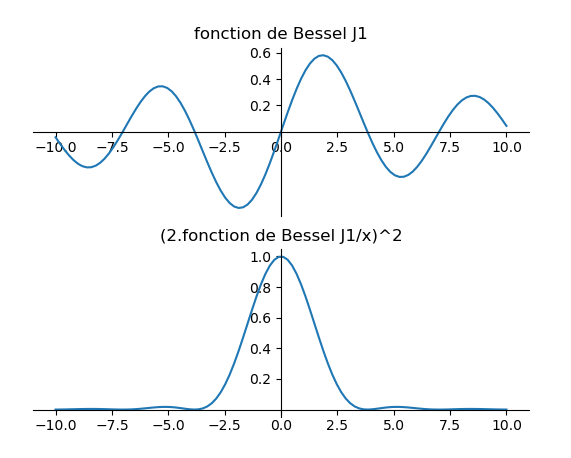
La fonction de Bessel J1
%%%%%%%%%%%%%%%%%%%% %ENSCR 20220907 % bessel_j1 et 4*(bessel_j1/z)^2 # -*- coding: utf-8 -*- # 202209 # on importe des bibliothèques, des fonctions from math import sin, pi from scipy.special import jv # pour pouvoir tracer des courbes, on a besoin de 'pyplot' dans la librairire 'matplotlib' from matplotlib import pyplot # temps maximal d'affichage # écrire 2.0 avec le point définit un nombre flottant (float) # écrire 2 définit un entier (int) # pour voir la différence essayer de calculer 1/2 et 1/2.0 ou 1/2. avec le point Xmin=-10.0 Xmax=10.0 # on définit les axes (x,y), auxquels on rajoutera les courbes ax = pyplot.axes(xlim=(Xmin, Xmax), ylim=(-0.7, 1.1)) # nombre d'échantillons NbEchantillons=101 # on définit les instants de calcul de la courbe abscisses=[Xmin+(Xmax-Xmin)*i/NbEchantillons for i in range(NbEchantillons+1)] #TEST: print(temps) # courbe de Bessel J1 macourbe=[jv(1,x) for x in abscisses] macourbe2=[4*(jv(1,x)/x)**2 for x in abscisses] #TEST: print(macourbe) # on rajoute la courbe sur le graphique ax.plot(abscisses,macourbe,abscisses,macourbe2) # on demande l'affichage pyplot.show() |
 |


