Analyse de Fourier

Responsable : J. Roussel

Analyse d'un signal carré

Analyse de Fourier

Supposons un signal temporel périodique $y(t)$ de période $T$. On a \[y(t)=y(t+T)\quad \forall t\] Toute l'information du signal se trouve donc dans un motif de durée $T$ qui se répète $f=1/T$ fois en une seconde. $f$ désigne la fréquence du signal.

Le théorème de Fourier énonce — sous certaines conditions mathématiques que l'on supposera valides ici — qu'un signal périodique de fréquence $f$ se décompose en une somme infinie de sinus et cosinus de fréquence $f$, $2f$, $3f$, etc. Formellement on a

\begin{equation} \boxed{\displaystyle y(t)=a_{0}+\sum_{n=1}^{\infty}c_{n}\cos(2\pi n ft+\varphi_{n}) } \quad\heartsuit \end{equation}

Il s'agit de la décomposition de Fourier d'un signal périodique.

• Le terme $a_{0}$ désigne la composante continue, c'est-à-dire la valeur moyenne du signal: \[ a_{0}=\frac{1}{T}\int_{0}^{T}y(t)\,\mathrm{d}t \]
• Le terme $c_{n}\cos(2\pi n ft+\varphi_{n})$ représente une harmonique de rang $n$. Les $c_{n}$ sont les coefficients de Fourier et leur valeur dépend de la forme du signal.

Lorsque l'on représente l'amplitude $c_n$ des harmoniques en fonction de leur fréquence $f_{n}=n\,f$, on obtient le spectre d'amplitude du signal.

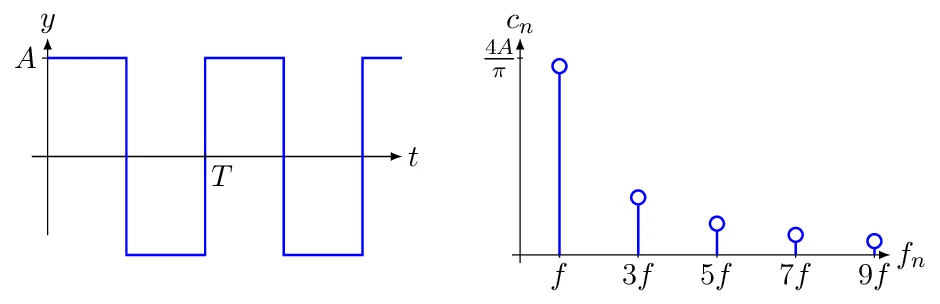
Théorème de Parseval — Pour un signal périodique décomposable en série de Fourier, on a l'égalité:

\begin{equation} \boxed{\displaystyle \overline{y(t)^{2}}={a_{0}}^{2}+\frac{1}{2}\sum_{n=1}^{\infty}{c_{n}}^{2} } \label{eq:theoreme_de_parseval} \end{equation}

où $\overline{y(t)^{2}}$ désigne la moyenne temporelle du signal au carré.

FFT

Le calcul d'un spectre se fait couramment à l'aide d'un algorithme inventé en 1965 et qui rencontra un très grand succès : la Transformée de Fourier Rapide, FFT pour les intimes (Fast Fourier Transform).

En TP, les oscilloscopes numériques calculent le spectre d'un signal à l'aide de cet algorithme. Pour cela, le signal affiché est enregistré sur la durée de la fenêtre d'observation ($\Delta t$), puis échantillonné (fréquence d'échantillonnage $f_\text{e}$).

Pour obtenir un spectre sur la largeur $[0,f_\text{max}]$ avec une bonne résolution, il faut respecter les conditions suivantes:

\begin{equation} \Delta t\quad\text{grand} \qquad\text{et}\qquad f_\text{e}>2f_\text{max}\quad\text{(critères de Shannon)} \end{equation}

Étude expérimentale d'un signal carré

1. Branchez la sortie 50 Ω du GBF sur la voie 1 (CH1) de l'oscilloscope.
2. Fixez la fréquence à f = 500 Hz et choisir un signal carré d'amplitude A = 2 V.
3. Appuyez sur CH1 pour faire apparaître le menu de la voie 1 : choisir le couplage AC.
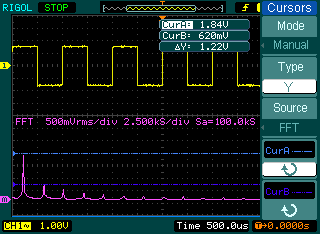
4. L'oscilloscope peut calculer en temps réel le spectre du signal. Appuyez sur Math $\blacktriangleright$ FFT puis placez Windows sur Hamming et Scale sur Vrms. L'oscilloscope donne le spectre avec en ordonnée la tension efficace $c_{n\;\mathrm{eff}}=c_n/\sqrt{2}.$
5. En pratique, pour obéir au critère de Shannon tout en cherchant à avoir une bonne résolution spectrale, il faut chercher à obtenir entre 5 et 10 périodes du signal sur l'écran.
6. On mesure les fréquences et les valeurs efficaces des harmoniques en utilisant les curseurs.
   -Pressez CURSOR $\blacktriangleright$ Mode et sélectionnez Manual.
   -Pressez Type pour sélectionner X ou Y.
   -Pressez Source pour sélectionner FFT. Déplacer les curseurs pour faire vos mesures.

Expérience n°1

Dans un premier temps, collectez les fréquences $f_n$ des 6 premières harmoniques. Entrez ces données dans Regressi™ et vérifiez qu'elles sont bien multiples impaires d'une fréquence fondamentale $f$ qu'on déterminera. Le résultat est-il cohérent ?

Expérience n°2

Ensuite collectez les coefficients de Fourier pour les 6 premières harmoniques.

Vérifiez que les $c_{n\;\rm eff}$ suivent la loi \[c_{n\;\rm eff}=\frac{4A}{\sqrt{2}\;\pi}\frac{1}{n}\] En déduire l'amplitude $A$ du signal carré (ne pas oubliez son incertitude). Le résultat est-il en accord avec l'affichage du GBF ?

Calculez la somme $S=\displaystyle \sum_{n}c_{n\;\mathrm{eff}}^{2}$. Le résultat est-il en accord avec la loi de Parseval ?

Réponse d'un filtre par analyse spectrale

Notion de filtrage

Lorsque l'on étudie la réponse fréquentielle d'un circuit, on branche une source alternative entre deux points d'un circuit (l'entrée du circuit) et on observe la réponse du circuit en mesurant une grandeur électrique en sortie du circuit. On forme alors un quadripôle.

En régime sinusoïdal, toutes les grandeurs oscillent de façon sinusoïdale à la même fréquence (On suppose ici que le quadripôle est linéaire, c'est-à-dire exclusivement constitué de dipôles linéaires). En notation complexe, les tensions d'entrée et de sortie s'écrivent \[ \underline{u_{\rm e}}(t)= \underline{U_{\rm e}}\,\mathrm{e}^{i2\pi f t} \qquad\text{et}\qquad \underline{u_{\rm s}}(t)=\underline{U_{\rm s}}\,\mathrm{e}^{i2\pi f t} \qquad\text{avec}\qquad i^2=-1 \] On mesure la réponse sortie/entrée en calculant le gain complexe en tension \[ \underline{H}(f) = \frac{\underline{u_{\rm s}}(t)}{\underline{u_{\rm e}}(t)} = \frac{\underline{U_{\rm s}}}{\underline{U_{\rm e}}} \] Ce nombre complexe donne une information à la fois sur le gain $G$ (rapport des amplitudes) et sur le déphasage sortie/entrée : \[ G=|\underline{H}|=\frac{U_{\rm s}}{U_{\rm e}} \qquad\text{et}\qquad \phi=\arg{\underline{H}} \] On obtient la courbe de réponse du quadripôle en traçant $G$ en fonction de la fréquence $f$. Suivant l'allure de $G(f)$ on donne un nom au quadripôle.

Ainsi, lorsque le signal d'entrée est périodique mais non sinusoïdal, chaque harmonique étant différemment atténuée et déphasée, on obtient à la sortie, un signal de même fréquence mais de forme différente. L'analyse harmonique des signaux en entrée et en sortie permet d'obtenir une information sur la réponse fréquentielle du filtre. En effet, si la tension d'entrée s'écrit \[ u_{\rm e}(t)=a_{0}+\sum_{n=1}^{\infty}c_{n,\,\rm e}\cos(2\pi nft+\varphi_{n}) \] alors chaque harmonique est, en sortie, atténuée et déphasée : \[ u_{\rm s}(t)=G(0)\times a_{0}\ +\sum_{n=1}^{\infty}G(f_n)\times c_{n,\rm e}\cos(2\pi nft+\varphi_{n}+\phi(f_n)) \] Il est donc possible de remonter à la réponse fréquentielle du filtre à partir des coefficients de Fourier des signaux en entrée et en sortie puisque

\begin{equation} \boxed{\displaystyle c_{n,\rm s}=G(f_n)\,c_{n,\rm e}} \end{equation}

Étude d'un filtre passe-bas

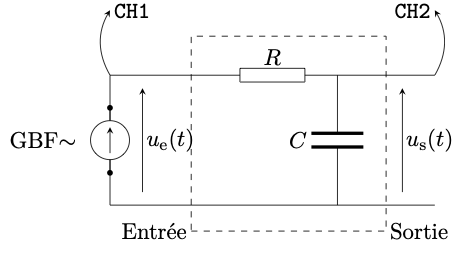
1. Réalisez le montage RC décrit ci-contre.
2. Envoyez la tension de sortie (aux bornes du condensateur) sur la voie 2 de l'oscilloscope.
3. Envoyez la tension d'entrée (sortie du GBF) sur la voie 1.

Observations et Mesures

1. Alimentez le circuit avec un signal sinusoïdal et vérifiez qualitativement qu'il s'agit d'un filtre passe-bas.
2. Envoyez maintenant une série d'impulsions. Pour cela, passez en mode PULSE. Ajustez la fréquence à 200 Hz, l'amplitude crête à crête à $V_{\mathrm{pp}}=5\,\mathrm{V}$ et la largeur des impulsions à $200\;\mathrm{\mu s}$. Placez-vous en mode AC pour éliminer toute composante continue.
   Le signal de sortie est-il de la même forme que celui en entrée ? Pourquoi ?
3. Collectez dans un tableau Regressi™ les amplitudes des harmoniques du signal d'entrée et de sortie ainsi que la fréquence correspondante.
4. Créez la grandeur $G=c_{ns}/c_{ne}$ et portez $G$ en fonction de la fréquence $f$. À l'aide d'une modélisation, déterminer la fréquence de coupure du filtre passe-bas.
5. Y-a-t-il adéquation avec la valeur théorique ?