Dessiner avec TikZ
TikZ est un outil que nous utilisons pour créer des figures directement dans le code source LaTeX.
Ci-dessous, un exemple LaTeX minimal, qui peut être réutilisé avec les codes TikZ qui suivent.
\documentclass[10pt]{minimal}
\usepackage[french]{babel} %typographie française
\usepackage[T1]{fontenc} %accents codés dans la fonte
\usepackage[utf8]{inputenc} %accents 8 bits dans le fichier
\usepackage{tikz} %pour les figures tikz
\usetikzlibrary{calc} %pour que tikz fasse des calculs
%\usetikzlibrary{arrows} %pour que tikz dessine des flèches comme on veut
%\usepackage{pgfplots} %package pgfplots si besoin
\begin{document}
\begin{tikzpicture}
\draw (0,0) -- (1,1) node [right] {Un segment};
\end{tikzpicture}
\end{document}
|
Un amplificateur, avec TikZ
%%%%%%%%%%%%%%%%%%%%
%ENSCR 20170128
%ALI amplificateur (ampli-op)
\begin{tikzpicture}
\draw (0,-1.5) rectangle (2,0.5);
%legende
\draw (0.3,0) node {$+$};
\draw (0.3,-1) node {$-$};
\draw (1.7,0) node {$\infty$};
%un triangle
\draw (1.3,-0.1) -- ++(30:0.2) -- ++(150:0.2) --cycle ;
\end{tikzpicture}
|
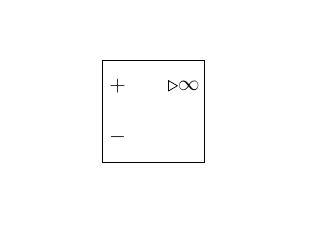 |
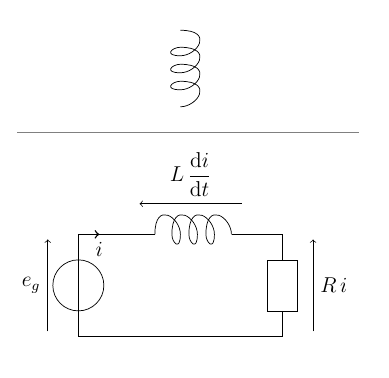
Une bobine, avec TikZ
%%%%%%%%%%%%%%%%%%%%
%ENSCR 20170303
%bobine, coil
\begin{tikzpicture}
%3 spires definies par des courbes de bezier et une boucle for
\foreach \r in {0,...,2}
{\draw[scale=1/3,shift={(0,-\r)}]
(0,0) .. controls ++(2,0) and ++(1,0) ..
++(0,-1.5) .. controls ++(-1,0) and ++(-0.5,0) ..
++(0,0.5);
}
%une demi-spire pour finir
\draw[scale=1/3,shift={(0,-3)}] (0,0) .. controls ++(2,0) and ++(1,0) .. ++(0,-1.5);
\end{tikzpicture}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%
%ENSCR 20170303
%bobine, dans un circuit
%on reprend la bobine précédente et on l'inclut dans un circuit
\begin{tikzpicture}
%circuit electrique: un rectangle
\draw (0,0) rectangle (4,2);
%source de tension
\draw (0,1) circle(0.5cm);
%resistance, remplie de blanc pour masquer le circuit
\draw[fill=white] (3.7,1.5) rectangle (4.3,0.5);
%la bobine
%le point de depart de la bobine est situe en (0,0)
%il faut la decaler pour la placer au bon endroit via le scope et le shift
%elle est originalement verticale: il faut la tourner de 90 degres
\begin{scope}[shift={(1.5,2)},rotate=90]
{%un rectangle blanc sous la bobine pour masquer le circuit
\draw[white,fill=white] (-0.2,0) rectangle (0.4,-1.5);
%3 spires definies par des courbes de bezier, via une boucle for
\foreach \r in {0,...,2}
{
\draw[scale=1/3,shift={(0,-\r)}]
(0,0) .. controls ++(2,0) and ++(1,0) ..
++(0,-1.5) .. controls ++(-1,0) and ++(-0.5,0) ..
++(0,0.5);
}
%une demi-spire pour finir
\draw[scale=1/3,shift={(0,-3)}] (0,0) .. controls ++(2,0) and ++(1,0) .. ++(0,-1.5);
}
\end{scope}
%fleches de tension et intensite
\draw[->] (-0.6,0.1) -- (-0.6,1.9) node [midway,left] {$e_g$};
\draw[->] (3.2,2.6) -- (1.2,2.6) node [midway,above] {$L\,\displaystyle\frac{\mathrm{d}i}{\mathrm{d}t}$};
\draw[->] (4.6,0.1) -- (4.6,1.9) node [midway,right] {$R\,i$};
\draw[thick,->] (0.4,2) -- +(0.01,0) node [below] {$i$};
\end{tikzpicture}
|
 |
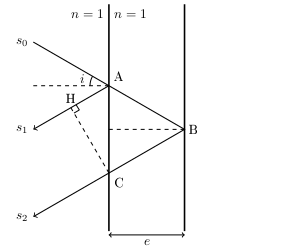
Une lame d'air, avec TikZ
%%%%%%%%%%%%%%%%%%%%
%ENSCR 20161015
%lame de verre faces parallèles
%deux lames situées en x=-1 et x=+1
%un rayon arrive sous l'incidence i
\begin{tikzpicture}[scale=1]
\pgfmathsetmacro{\angleincidence}{30}
\pgfmathsetmacro{\xS}{-3}
\pgfmathsetmacro{\yS}{2}
\pgfmathsetmacro{\yA}{\yS-2*tan(\angleincidence)}
\pgfmathsetmacro{\yB}{\yA-2*tan(\angleincidence)}
\pgfmathsetmacro{\yC}{\yB-2*tan(\angleincidence)}
\pgfmathsetmacro{\yD}{\yA-2*tan(\angleincidence)}
\pgfmathsetmacro{\yE}{\yC-2*tan(\angleincidence)}
\coordinate (S) at (\xS,\yS);
\coordinate (A) at (-1,\yA);
\coordinate (B) at (1,\yB);
\coordinate (C) at (-1,\yC);
\coordinate (D) at (-3,\yD);
\coordinate (E) at (-3,\yE);
%projection orhtogonale de C sur [AD]
\coordinate (H) at ($(A)!(C)!(D)$);
%symbole d'orthogonalité
%on part de H sur le segment AH, on se déplace de 0.2AH et on tourne de 45 degre.
\coordinate (HH) at ($(H)!0.2!-45:(A)$);
%lame
\draw[very thick] (-1,-3) -- (-1,3)
node [below left] {$n=1$} node [below right] {$n=1$};
\draw[very thick] (1,-3) -- (1,3) ;
%epaisseur
\draw[<->] (-1,-3.1) -- (1,-3.1) node [midway,below] {$e$};
%rayon incident
\draw[thick,->] (S) node [left] {$s_{0}$}
-- (B) node [right] {B}
-- (E) node [left] {$s_{2}$};%rayon reflechi sur la 2e face
\draw[thick,->] (A) node [above right] {A}
-- (D) node [left] {$s_{1}$};%rayon reflechi sur la 1e face
%normales aux faces
\draw[dashed] (A) -- +(-2,0);
\draw[dashed] (B) -- +(-2,0);
%perpendiculaire
\draw[dashed] (C) node [below right] {C}
-- (H) node [above] {H};
%symbole d'orthogonalite
\draw (HH) -- ($(H)!(HH)!(C)$);
\draw (HH) -- ($(A)!(HH)!(D)$);
%angle i
\draw (A) +(-0.5,0) arc(0:-\angleincidence:-0.5);
\path (A) +(-0.7,0.2) node {$i$};
\end{tikzpicture}
|
 |
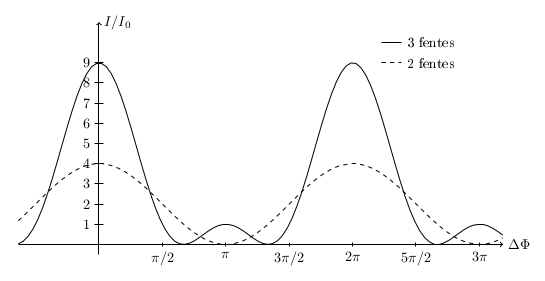
Comparaison des interférences avec 2 ou 3 fentes d'Young, avec TikZ
%%%%%%%%%%%%%%%%%%%%
%ENSCR 20160112
%Intensité obtenue après 2 ou 3 fentes de type Young (interférences)
\begin{tikzpicture}[yscale=0.3]
%axes
\draw[->] (0,-0.5) -- (0,11) node [right] {$I/I_0$};
\draw[->] (-2,0) -- (10,0) node [right] {$\Delta\Phi$};
%graduations
\foreach \y in {1,2,...,9} \draw (0.1,\y) -- (-0.1,\y) node [left] {$\y$};
\draw (1.57,0.1) -- (1.57,-0.1) node [below] {$\pi/2$};
\draw (3.14,0.1) -- (3.14,-0.1) node [below] {$\pi$};
\draw (4.71,0.1) -- (4.71,-0.1) node [below] {$3\pi/2$};
\draw (6.28,0.1) -- (6.28,-0.1) node [below] {$2\pi$};
\draw (7.85,0.1) -- (7.85,-0.1) node [below] {$5\pi/2$};
\draw (9.42,0.1) -- (9.42,-0.1) node [below] {$3\pi$};
%courbes 3 fentes (le \x r précise que les angles sont en radians)
%les {} sont utiles pour faire faire les calculs
\draw plot [domain=-2:10, samples=100] (\x,{(1+2*cos(\x r))^2});
%courbe 2 fentes
\draw[dashed] plot [domain=-2:10,samples=100] (\x,{2*(1+cos(\x r))});
%legende
\draw (7,10) -- (7.5,10) node [right] {3 fentes};
\draw[dashed] (7,9) -- (7.5,9) node [right] {2 fentes};
\end{tikzpicture}
|
 |
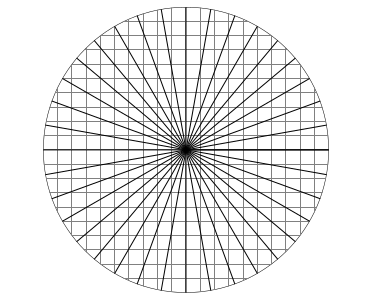
Un cercle trigonométrique gradué
%%%%%%%%%%%%%%%%%%%%
%ENSCR 20181018
%un cercle trigonométrique, gradué en angles, abscisses et ordonnées
\begin{tikzpicture}[scale=4]
\clip (0,0) circle(1);
\draw (0,0) circle(1);
\draw (0,1) -- (0,-1);
\draw (1,0) -- (-1,0);
\draw[help lines,xstep=0.1,ystep=0.1] (-1,-1) grid (1,1);
\foreach \x in {0,10,...,360} \draw[thick] (0,0) -- +(\x:1);
\end{tikzpicture}
|
 |


