Fluid Mechanics

Supervisors: O.Frantz, J.Geandrot

This practical work aims to study some properties of fluids, inviscid or viscous.

Physical laws

A fluid is a substance that flows. It possesses the ability to take on the shape of the container. Both the liquid and gas phases are included as well as plasmas and to some extent, plastic solids.

Conservation of flow

The flow volume $Q_\mathcal{V}$ is the volume $\mathcal{V}$ flowing through a cross-section $S$ per unit time :

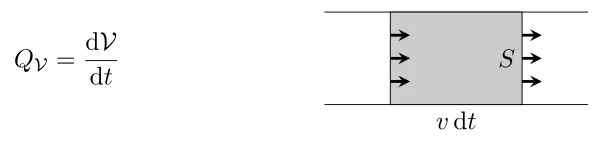
During $\mathrm{d}t$, a quantity of fluid flows through section $S$. What is the traveled distance $\mathrm{d}\ell$ of the last fluid particle that passes through $S$ between 0 and $\mathrm{d}t$? According to the definition of the velocity, it has traveled $\mathrm{d}\ell=v\,\mathrm{d}t$. The volume that passes through $S$ is therefore $\mathrm{d}\mathcal{V}=\mathrm{d}\ell\,S=v\,\mathrm{d}t\,S$ and the flow rate \begin{equation}\boxed{ Q_\mathcal{V}=\frac{\mathrm{d}\mathcal{V}}{\mathrm{d}t}=v\,S } \quad \heartsuit\end{equation}

If no particle disappears during the flow and if the fluid is incompressible, the flow volume remains constant : \begin{equation}\boxed{v\,S=\mathrm{cste}} \quad \heartsuit\end{equation}

Bernoulli’s principle

For a steady flow of a non-viscous, incompressible fluid, between two points A and B of the same streamline, with $p$ as pressure, $\rho$ as density and $v$ as speed : \begin{equation}\boxed{p_A+\dfrac{1}{2}\,\rho\,{v_A}^2+\rho\,g\,z_A=p_B+\dfrac{1}{2}\,\rho\,{v_B}^2+\rho\,g\,z_B} \quad \heartsuit\end{equation}

This law expresses the conservation of energy density (each term is expressed (in SI base units) in $\mathrm{J.m^{-3}}$). It mixes together elastic, kinetic and gravitational energies.

Viscosity

The dynamic viscosity of a fluid expresses its resitance to shearing flows, where adjacent layers move parallel to each other with different speeds. It corresponds to the concept of thickness. Its unity is Pa.s (pascal.second) and its symbol is $\mu$. It strongly depends on temperature for liquid phases.

Stokes’ law

Georges Stokes got interessed in the drag force exerted on spherical objects in a viscous fluid with very small Reynolds numbers. In this case, the flow is mostly governed by viscosity and one can neglect inertial effects.

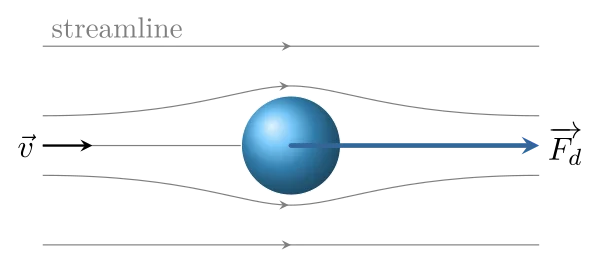
The drag force $F_d$ exerted on spherical objects (radius $r$) with very small Reynolds numbers in a viscous fluid follows the Stokes’law : \begin{equation}\boxed{\overrightarrow{F_d}=6\pi\mu r\,\vec{v}}\end{equation}

where $\vec{v}$ represents the flow speed according to the sphere and far from it.

The Reynolds number $\mathcal{R}_e$ (which is ratio of inertial forces to viscous forces) must be \begin{equation}\heartsuit \quad \boxed{\mathcal{R}_e=\dfrac{\rho\,v\,d}{\mu}} \qquad \begin{cases} \mathcal{R}_e\ll 1 &\text{viscous flow}\\ \mathcal{R}_e\gg 1 &\text{non-viscous flow} \end{cases}\end{equation} $\rho$ is the density of the fluid, $v$ the velocity of the flow and $d$ the ball diameter. With a required precision better than 1%, Reynolds number must respect $\mathcal{R}_{e}<0{.}3$ for Stokes’law to be valid.

Falling velocity

Let us list external forces acting on a ball falling through a fluid, which is immobile in the laboratory reference frame :

Weight :	$\dfrac{4}{3}\,\pi\,r^3\,\rho_b\,g$	where $\rho_b$ is the density of the ball;
Buoyant force :	$\dfrac{4}{3}\,\pi\,r^3\,\rho\,g$	thanks to Archimedes’principle;
Drag force :	$6\pi\,\mu\,r\,v$	where $v$ is the ball velocity.

Please note that the drag force points in the opposite direction of velocity. In the laboratory frame of reference, which is supposed to be galilean, the second law of Newton gives \begin{equation}\dfrac{4}{3}\pi r^3\,\rho_b\,\dfrac{\mathrm{d}{v}}{\mathrm{d}{t}} = \dfrac{4}{3}\pi r^3\,(\rho_b-\rho)\,g-6\pi\,\mu\,r\,v\end{equation}

With an initial velocity equals to zero, the solution of this differential equation is \begin{equation}v=\dfrac{2\,g\,(\rho_b-\rho)}{9\,\mu}\,r^2\left(1-\mathrm{e}^{-t/\tau}\right) \qquad\text{avec}\qquad \tau=\dfrac{2\,\rho_b}{9\,\mu}\,r^2\end{equation}

When $t>3\tau$, the exponential is negligible compared to 1 and the velocity becomes \begin{equation}\boxed{v_\infty=\dfrac{2\,g\,(\rho_b-\rho)}{9\,\mu}\,r^2}\end{equation}

Knowing this asymptotic speed, we can deduce the fluid viscosity.

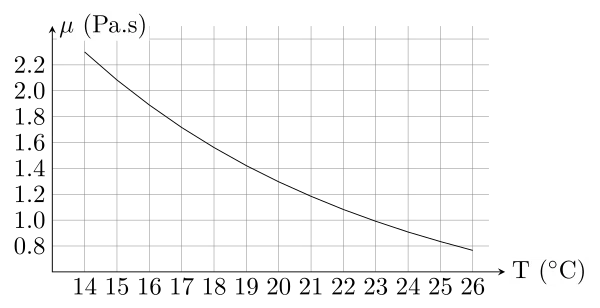
Note that viscosity stongly depends on temperature (through molecular agitation). The chart below shows this dependency for glycerol.

Flow in a narrow pipe, Hagen-Poiseuille equation

At the bottom of a container, which diameter is D, a horizontal, long and narrow pipe, which diameter is $d\ll D$, let water flows.

When the flow is stopped, pressure in liquid only depends on elevation $z$. Therefore, the free surface, which pressure is equal to atmospheric one, is necessarily an horizontal plane. That is why the liquid level is the same in all the vertical tubes and in the main container.

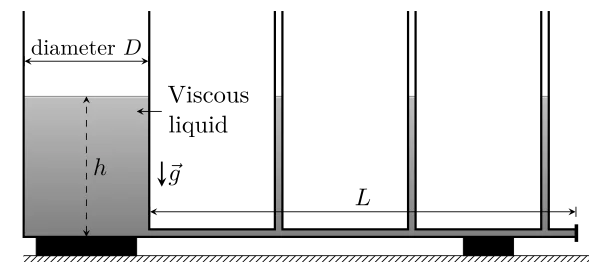
When the liquid flows through the narrow pipe, pressure is not uniform anymore. Because of viscosity, it is stronger upstream (at the bottom of the container) than downstream (at the end of the pipe). The pressure difference $(p_\mathrm{u}-p_\mathrm{d})$ is called pressure drop $\Delta{p}$. If the flow is slow enough, pressure drops down linearly along the pipe. Poiseuille showed that, where $Q_{\mathrm{v}}$ is the volumetric flow rate ($\mathrm{m^3.s^{-1}}$), \begin{equation}\boxed{ \Delta{p} =\frac{128\,\mu L}{\pi d^4}\,Q_{\mathrm{v}} }\end{equation}

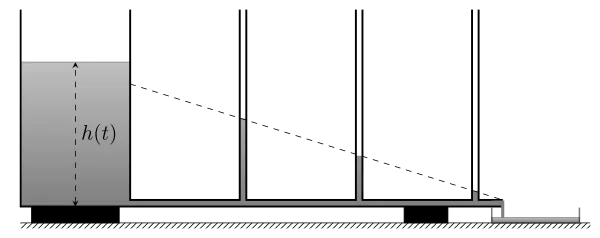
In the container, the fluid flows more slowly than in the pipe. As a first approximation, it can be considered that it is static and that pressure at its bottom is hydrostatic : $p_{\mathrm{u}}=p_{\mathrm{atm}}+\rho\,g\,h$. At the end of the pipe, pressure is $p_{\mathrm{d}}=p_{\mathrm{atm}}$. Finally, \begin{equation}\boxed{ \rho\,g\,h=\dfrac{128\,\mu\,L}{\pi\,d^4}Q_{\mathrm{v}} }\end{equation}

Please note that there may be no vertical tubes over the long and narrow pipe during the experimentation.

Emptying law

Let us look for the equation giving the water level $h$ overt time knowing that initial height is $h(t=0)=h_0$. According to Hagen-Poiseuille law, volumetric flow rate is proportionnal to the water level $h$ : \begin{equation}Q_{\mathrm{v}}=\frac{\rho\,g\,\pi\,d^4}{128\,\mu\,L}\,h\end{equation} Therefore, between $t$ and $t+\mathrm{d}t$, the height is dropping from $h(t)$ to $h(t+\mathrm{d}t)$ and the volume loss is equal to : \begin{equation}\mathrm{d}V=\frac{\pi\,D^2}{4}[h(t)-h(t+\mathrm{d}t)]\end{equation} By definition of the volumetric flow rate : \begin{equation}\mathrm{d}V =Q_{\mathrm{v}}\,\mathrm{d}t =\frac{\rho\,g\,\pi\,d^4}{128\,\mu\,L}\,h\,\mathrm{d}t\end{equation} This leads to the differential equation below : \begin{equation}\dfrac{h(t+\mathrm{d}t)-h(t)}{\mathrm{d}t} =\dfrac{\mathrm{d}h}{\mathrm{d}t} =-\dfrac{\rho\,g\,d^4}{32\,\mu\,L\,D^2}\,h\end{equation} which solution is \begin{equation} \boxed{h(t)=h_0\,\mathrm{e}^{-t/\tau}} \qquad\text{with}\qquad \boxed{\tau=\frac{32\,\mu\,L\,D^2}{\rho\,g\,d^4}} \qquad\heartsuit \end{equation} As a consequence, measuring the time constant $\tau$ gives the dynamic viscosity of water.

Equipment

Precision manometer

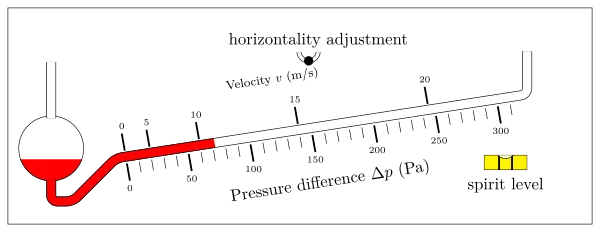
The precision manometer directly uses the Bernoulli law. The pressure difference between the two ends is converted to an altitude difference, by means of the slope of the tube. Important : do not to forget to adjust the horizontality of the manometer before any measurement. The pipes connected to both ends (fragile glass) shall never be removed from there!

Pitot/Prandtl tube

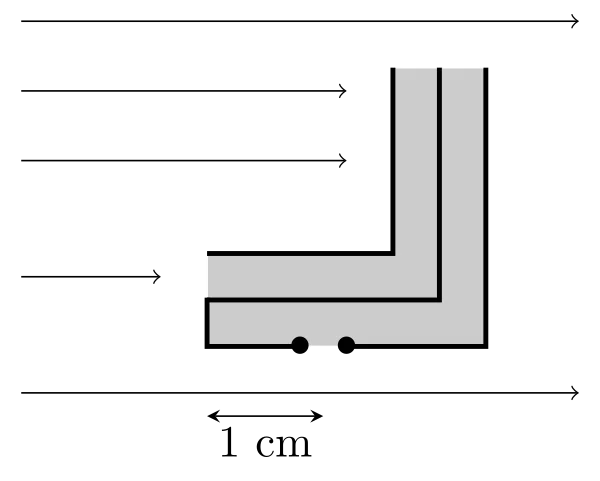
The Pitot or Prandtl tube measures the fluid velocity. It consists of two tubes, one facing the flow measuring the "total" pressure $\mathbf{p_0+\boldsymbol{\rho}\,v^2/2}$ and the other open perpendicularly measuring the static pressure $\mathbf{p_0}$. Since the holes are substantially on the same streamline, the Bernoulli law leads to \begin{equation}\boxed{v=\sqrt{2\Delta{p}/\rho}}\end{equation}

Therefore, on the precise pressure gauge (pressure difference measuring apparatus), there is also a velocity scale, used only when the Pitot tube is associated with the measurement.

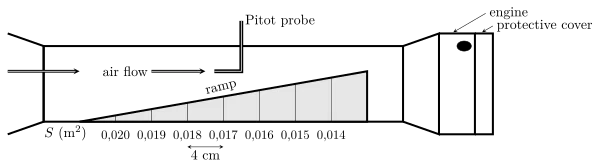
Bernoulli ramp

A Bernoulli ramp is mounted within the wind tunnel. The graduation of this ramp gives the cross-section through which the fluid flows. This cross-section goes from $200~\mathrm{cm^2}$ to $150~\mathrm{cm^2}$. A Pitot probe, connected to the manometer, gives access to the fluid velocity which changes over the cross-section.

Constriction and Venturi effect

A constricting pipe may be connected behind the blower motor via a variable nozzle section, by removing the protective cover (never remove it when the engine is running!). Please note that the connection of the nozzle with the blower is not well assured. Check at any moment that the parts are properly attached.

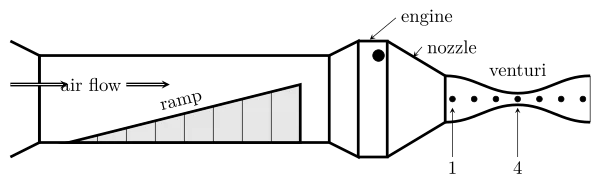
The pipe has 7 numbered holes to collect the static pressure. Between two points A and B of the Venturi tunnel, whose diameter is D and whose cross-section is $S=\pi D^2/4$, the flow conservation law and the Bernoulli law lead to \begin{equation}\left. \begin{array}{r} {D_A}^2\,v_A={D_B}^2\,v_B \\ p_A+\rho\,{v_A}^2/2=p_B+\rho\,{v_B}^2/2 \end{array} \right\} \Rightarrow {v_A}^2={2\,\frac{p_B-p_A}{\rho\,(1-(D_A/D_B)^4)}}\end{equation} and with obvious notations$\boxed{{v}^2=k\,\Delta{p}}$
Diameters of the pipe at each outlet : \begin{equation}\begin{array}{|*{7}{c|}} \hline D_1 & D_2 & D_3 & D_4 & D_5 & D_6 & D_7 \\ \hline 100~\mathrm{mm} & 95~\mathrm{mm} & 70~\mathrm{mm} & 50~\mathrm{mm} & 70~\mathrm{mm} & 95~\mathrm{mm} & 100~\mathrm{mm} \\ \hline \end{array}\end{equation}

Tasks

Preparation

Falling balls through glycerol

Given that the order of magnitude of the viscosity of glycerol is about 1 Pa.s, calculate the Reynolds number for each ball falling through glycerol, by using an estimated falling speed and glycerol density $\rho=1\,261~\mathrm{kg.m^{-3}}$.

Evaluate the time constant of the movement for each ball.

Bernoulli ramp and Venturi pipe

How do flow speed and pressure evolve in a narrowing pipe? Justify.

The two holes of the Pitot probe are distant from 1 cm. Each graduation is distant from 4 cm. Evaluate the uncertainty on the cross-section. (Which hole of the probe must be over the graduation?)

Manipulations

---

Glycerol viscosity : Falling balls through glycerol (30’)

First of all, we want to evaluate Glycerol viscosity. We will let steel balls fall through glycerol in a long tube (along the wall) and measure the time travel between two marks to deduce the limit velocity.

1. Get a stopwatch or use the online stopwatch :

   http ://online-stopwatch.chronme.com/

2. Drop one ball in the tube and measure, using the stopwatch, the travel time between two marks. Use a magnet to stop the fall, before the ball reaches the bottom of the tube, and get it out. Make sure the ball approximately falls at the center of the tube, otherwise it would be more slowed down than expected.
3. Repeat this for 6 different sized balls (diameters : 20.0 mm; 12.6 mm; 6.35 mm; 5.55 mm; 4.75 mm and 4.00 mm).
4. For each ball, repeat the measure twice and let Regressi calculate the mean value $\overline{t}$ and its uncertainty $\Delta t=t_{\mathrm{max}}-t_{\mathrm{min}}$.
5. Let Regressi calculate the falling velocity $v$ and its uncertainty.

Plot the limit velocity versus $r^2$ and show that Stokes law is valid only for some balls. Given that $\rho_b=7\,850\;\mathrm{kg.m}^{-3}$ and $\rho=1\,261\;\mathrm{kg.m^{-3}}$, deduce glycerol dynamic viscosity $\mu$ and its uncertainty. Compare with thoeretical one.

---

Water viscosity : Emptying of a tank through a long and narrow pipe (30’)

We want to determine tap water viscosity. Proceed as follows :

1. Stop the flow at the end of the pipe and put water in the container ($\simeq 25$ cm).
2. Get a stopwatch and get used to it before proceeding.
3. Let water flows and start counting when its level reaches $h=$ 20 cm. Record each moment when $h=$ 18 cm, 16 cm, 14 cm, 12 cm et 10 cm.

Draw $\ln h(t)$ according to $t$. Is Hagen-Poiseuille equation valid? Deduce the value of water viscosity $\mu$, knowing that $L=1~\mathrm{m}$, $D=6{.}1~\mathrm{cm}$ et $d=4~\mathrm{mm}$.

---

Bernoulli ramp (30’)

Now we want to check flow continuity and Bernoulli equation.

Make sure you position the Pitot probe parallel to the stream.

For each graduation of the ramp, collect the pressure difference between the two probe arms. The probe must be at the center of the flow.

Looking at the manometer, do not forget to take into account the position of the fluid at equilibrium : the zero is not necessarily calibrated. Also collect the measurement uncertainties : which hole of the pressure probe must be placed above the cross-section graduation? what is the precision of the graduation? ...

Let Regressi convert the pressure difference into velocity.

Provide a graph and a table of velocity $v$ according to inverse of section.

Is the volume flow constant? Explain any differences.

---

Constriction and Venturi effect (30’)

Quickly check the evolution of pressure in the Venturi tunnel.

Is the square of speed proportional to the pressure difference?

Protocol :

1. Start the engine and choose a speed by adjusting the potentiometer.
2. Place the anemometer at the end of the tunnel and measure velocity when the flow is steady. Be careful, the measurement uncertainty is high. Try to collect several speeds by changing the position of the probe.
3. Measure pressure difference between points 1 and 4.

Repeat these operations with different speeds.

Provide the graph and table of $v^2$ according to $\Delta{p}$.

Do not forget to fill in the uncertainties.

Is proportionality verified on the full range of speed?

Explain any differences. Which hypothesis are questionable?

Equipment

• 6 steel balls ;
• a stopwatch ;
• a magnet ;
• a Hagen-Poiseuille lab kit ;
• a thermometer ;
• an anemometer ;
• a Pitot-Prandtl probe ;
• a wind tunnel ;
• a Bernoulli ramp ;
• a nozzle ;
• a Venturi pipe.