TP-cours : circuit RLC en régime forcé
Objectifs :
- Étudier la réponse d'un circuit RLC soumis à une tension variable ;
- Découvrir la notion de filtre et de fonction de transfert.
Un peu de théorie
Le résistor, la bobine et le condensateur ne se comportent pas de la même façon selon la fréquence imposée. Leurs impédances décrivent ce comportement ($\omega=2\pi\,f$) : \[Z_R=R \qquad Z_L=j\,L\omega \quad\text{et}\quad Z_C=\cfrac{1}{j\,C\omega}\]
Ainsi, la résistance ne dépend pas de la fréquence : $u=R\,i$.
Aux basses fréquences, la bobine présente une faible impédance : comme un interrupteur fermé (un fil), l'intensité circule facilement et la tension est proche de zéro.
Aux basses fréquences, le condensateur présente une très forte impédance :
comme un interrupteur ouvert, l'intensité circule très mal et est proche de zéro.
À haute fréquence, la bobine présente une forte impédance : comme un interrupteur ouvert, l'intensité circule très mal et est proche de zéro.
À haute fréquence, le condensateur présente une très faible impédance :
comme un interrupteur fermé (un fil), l'intensité circule facilement et la tension est proche de zéro.
Quand on associe ces composants de base, on peut combiner les différents comportements
pour réaliser des filtres : passe bas, passe haut, passe bande, réjecteur de bande.
Le but de ces filtres est de ne conserver du signal d'entrée que ce qui est jugé intéressant.
Dans la suite de ce TP-cours, on étudie la réponse d'un circuit RLC lorsqu'on le soumet à une tension alternative et qu'on mesure la tension aux bornes de la résistance (ch. schéma ci-dessous).
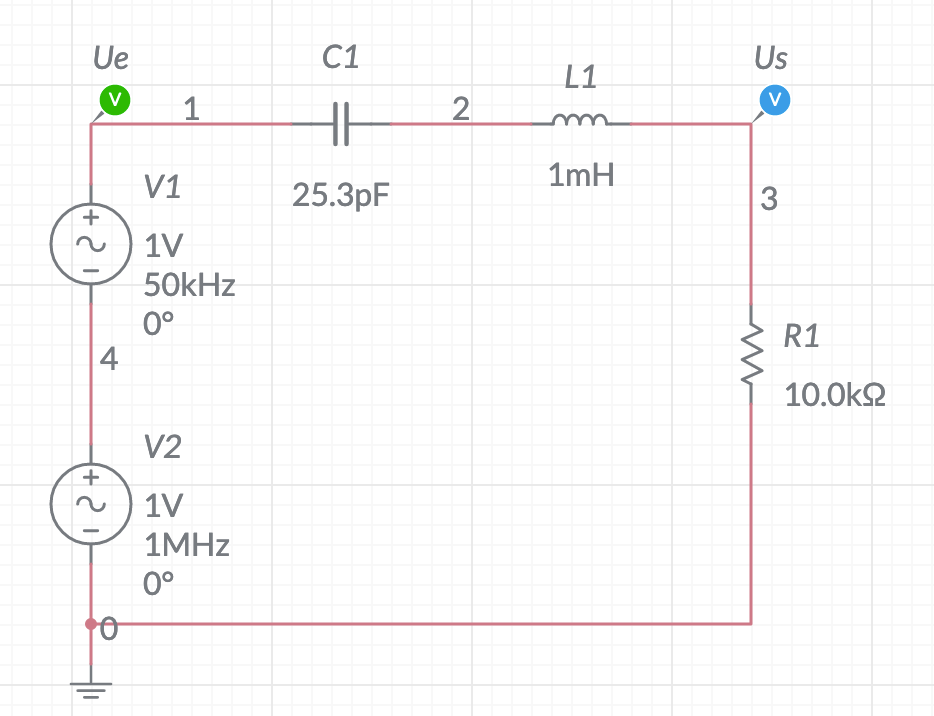
Si on appelle $e$ la tension aux bornes du générateur, $i$ l'intensité qui circule dans le circuit, l'impédance du circuit est la somme des impédances des trois composants en série : \[Z=\cfrac{e}{i}=R+j(L\omega-1/C\omega)\]
En conséquence, \[u_R=R\,i=\cfrac{R}{Z}\,e=\cfrac{jRC\omega}{(1-LC\omega^2)+jRC\omega}\,e\] En module, \[U_R=\cfrac{RC\omega}{\sqrt{(1-LC\omega^2)^2+(RC\omega)^2}}\,E\] En étudiant les variations de $U_R$ en fonction de la pulsation, on s'aperçoit que $U_R$ tend vers zéro quand $\omega\to 0$ et $\omega\to\infty$. $U_R$ est maximal pour la pulsation de résonance $\omega_0=\cfrac{1}{\sqrt{LC}}$. Il s'agit d'un filtre passe bande.
Réalisation du montage
Rendez-vous à l'adresse http://www.multisim.com, puis construisez le circuit RLC série avec les composants suivants :
- $C = 10\,\mathrm{nF}$;
- $L = 1\,\mathrm{mH}$;
- $R = 100\,\Omega$;
- deux sources sinusoïdales en série d'amplitude $1\,\mathrm{V}$ et de fréquences respectives $50\,\mathrm{kHz}$ et $1\,\mathrm{MHz}$.
On désire visualiser la tension d'entrée (issue de l'association des sources) et la tension aux bornes de la résistance. Placez alors les sondes de tension aux endroits adéquats.
Analyse fréquentielle
Simulation
On réalise une analyse fréquentielle (AC SWEEP), c'est-à-dire qu'on veut analyser le comportement du circuit quand la fréquence varie (et non le temps).
- Fixer la plage de fréquences entre 10 kHz et 10 MHz.
- Lancer l'analyse.
- N'afficher que la tension aux bornes de la résistance.
- Si la réponse fréquentielle n'est pas bien lissée (elle a un aspect de lignes brisées), augmenter la résolution en jouant sur le nombre de points par décade ("Points per Decade").
Questions
- Quel type de filtre est réalisé ?
- Quelle est la valeur de la fréquence centrale $f_0$ ? Comparer avec la valeur théorique $f_0=\frac{1}{2\pi\sqrt{LC}}$.
- Quelles sont les fréquences $f_2$ et $f_1$ qui correspondent à une amplitude maximum divisée par $\sqrt{2}$ ?
Calculer $\Delta{f}=f_2-f_1$ la bande passante du circuit. - En déduire le facteur de qualité $Q=f_0/\Delta{f}$ et comparer à la valeur théorique $Q=\frac{1}{R}\sqrt{\frac{L}{C}}$.
- Mesurer la nouvelle bande passante lorsque la résistance est divisée par deux. Conclure.
Analyse temporelle
Simulation
On veut visualiser à quoi ressemble les signaux dans le temps (Transient).
- Régler le temps d'analyse sur 0,2 ms. Régler le Maximum time step en mode "Manual" à $1 \times 10^{-7}\,\mathrm{s}$.
- Afficher les tensions d'entrée et aux bornes de la résistance.
- Modifier l'échelle horizontale (Zoomer avec la molette de la souris quand vous êtes sur l'axe horizontal) pour n'afficher que quelques périodes (entre 0,1ms et 0,11ms par exemple).
- Augmenter éventuellement la précision de l'analyseur (diminuer le Time Step) si les tensions ne sont pas bien lissées (si elles ont un aspect de lignes brisées).
Remarque : si on observe les tensions à un temps proche de zéro, on s'aperçoit qu'il existe un régime transitoire, qui disparaît rapidement. L'objet de ce TP n'est pas d'étudier ce régime transitoire et il est donc nécessaire de ne visualiser les tensions que lorsque ce régime a totalement disparu.
Questions
- À quoi ressemblent la tension d'entrée et la tension aux bornes de la résistance ? Expliquer ce qui s'est passé.
- Calculer la valeur de capacité qui permet d'obtenir une fréquence centrale adaptée à la récupération du signal de fréquence la plus élevée uniquement.
- Visualiser les mêmes tensions avec cette nouvelle valeur de $C$ et conclure.
Exercice : filtre passe bas
On conserve le circuit précédent mais on supprime la bobine.
Quel est le type de filtre réalisé aux bornes de la résistance ? Et aux bornes du condensateur ? Simuler pour comprendre.
La pulsation de coupure vaut $\omega_c=1/RC$.
Choisir la pulsation de coupure la plus adéquate permettant de séparer les deux fréquences présentes dans la tension d'entrée (sachant que $R=100\,\mathrm{\Omega}$).
En déduire la valeur à donner au condensateur.
Quelle fréquence récupère-t-on aux bornes du condensateur? et aux bornes de la résistance ?
Simuler pour comprendre: visualiser chacune des deux tensions pour confirmer vos hypothèses et conclure.
Réexprimer le module $U_R$ en fonction de $E$ en tenant compte de $L=0$.
Étudier le comportement de $U_R$ à basse et haute fréquence.
Retrouver l'expression de la fréquence de coupure, sachant qu'elle est obtenue quand le gain maximal $\left(\dfrac{U_{R_{\mathrm{max}}}}{E}\right)$ a été divisé par $\sqrt{2}$.


