Ondes centimétriques

Responsables : O.Frantz, J.Geandrot

Manipulation des fentes d'Young

❮ ❯

Tests de la polarisation de l'onde avec la grille grossière

❮ ❯

Manipulation de la loi de Malus avec la grille fine

❮ ❯

Lorsqu’on s’aperçoit que la valeur observée pour la vitesse de la lumière et la valeur apparaissant dans les équations de propagation du champ électrique sont identiques Maxwell interprète, dès 1865, les ondes lumineuses comme des ondes électromagnétiques. Ses hypothèses sont confirmées 20 ans plus tard par les expériences de Hertz. Depuis, de nombreux physiciens se sont attachés à montrer l’identité de nature entre les ondes hertziennes et les ondes lumineuses, en montrant expérimentalement leurs similitudes.

Dispositif expérimental et théorie

Émetteur/Récepteur

L’émetteur utilise une diode Gunn couplée à une cavité résonante. L’onde électromagnétique (hertzienne) émise est polarisée rectilignement par le cornet émetteur. Elle est monochromatique de fréquence d’environ 10 GHz. La tension aux bornes du récepteur est amplifiée et rectifiée. Remarque : le récepteur (antenne ou cornet) capte l’onde incidente selon une direction privilégiée. Ainsi, seule la projection du champ selon cette direction est mesurée.

Attention, il y a deux types de récepteurs : un cornet et une antenne. L’antenne capte les signaux venant de toutes les directions alors que le cornet est très directif.

La tension affichée est proportionnelle à l’intensité de la composante de l’onde hyperfréquence reçue, donc au carré de la composante du champ électrique reçue, hors saturation. On la mesure sur la sortie DC de l’amplificateur à l’aide d’un voltmètre. Pour rester hors saturation, la tension doit être inférieure à 10 V. Assez loin de l’émetteur, on peut considérer que l’onde est plane. On veille à garder une distance maximale entre l’émetteur et le récepteur.

Attention: L'émetteur peut moduler le signal émis. Veillez à ce que cette modulation soit désactivée en positionnant le commutateur sur 0 (parmi les 3 positions possibles INT, 0 et EXT).

Ondes hertziennes

Les équations de Maxwell combinées débouchent sur l’équation d’onde de D’Alembert. Les champs électriques et magnétiques ont une structure ondulatoire : ils se propagent à la vitesse $c=1/\sqrt{\varepsilon_0 \mu_0}$, indépendante du référentiel. Dans les milieux linéaires, comme l’air, le champ magnétique est en outre relié simplement au champ électrique, ce qui implique que l’étude seule de ce dernier suffit. Notons enfin que la densité d’énergie électromagnétique transportée est proportionnelle au carré de l’amplitude des champs.
Si on se limite à l’étude des ondes progressives planes monochromatiques (OPPH) de fréquence $\nu$ se propageant suivant l’axe $(Oz)$ , le champ électrique peut s’écrire selon \begin{equation}\overrightarrow{E}= \left(\begin{array}[c]{l} %\begin{systsimple} E_x = E_{x0}\,\cos(2\pi\,\nu\,(t-z/c)+\varphi_{x0}) \\ E_y = E_{y0}\,\cos(2\pi\,\nu\,(t-z/c)+\varphi_{y0}) \\ E_z = 0 \end{array}\right)\end{equation} Le champ est transverse (perpendiculaire à la direction de propagation) et polarisé généralement elliptiquement (sa direction varie dans le temps en suivant une ellipse).

La polarisation rectiligne ($\varphi_{x0}=\varphi_{y0}$) désigne le cas où le champ garde une direction constante. C’est un cas particulier intéressant car l’étude des ondes se simplifie :

Ondes stationnaires

Lorsqu’une onde électromagnétique se réfléchit, elle se superpose ensuite à l’onde incidente. On obtient, lorsque certaines conditions sont réunies, des ondes stationnaires. Ces ondes présentent des nœuds (amplitude nulle) et des ventres (amplitude maximale). Le phénomène n’est plus propagatif.

Lorsqu’une corde, dont une extrémité est fixée, est agitée, on observe souvent ce phénomène d’ondes stationnaires.

Polariseur/Analyseur - Loi de Malus

Le polariseur est un dispositif simple (par ex : une grille) qui permet d’obtenir des ondes polarisées rectilignement, que ce soit dans le visible ou le domaine hertzien, en ne laissant passer qu’une composante vectorielle de l’onde (direction passante) et en absorbant les autres. Les électrons libres du métal ne pouvant être mis en mouvement que le long de la grille, ils vont absorber spécifiquement l’énergie de la partie de l’onde dirigée le long de la grille et laisser passer le reste. Ainsi, à partir d’une onde elliptique, on obtient une onde rectiligne :

Remarquons qu’à partir d’une onde rectiligne, on ne conserve que la projection de l’onde incidente sur la direction passante du polariseur.

Ceci permet de faire fonctionner le polariseur en analyseur : il va bloquer totalement une onde sa direction passante est perpendiculaire à la polarisation de l’onde incidente (positions dites croisées) et laisser passer un maximum de l’onde incidente lorsqu’il est dans une position parallèle.

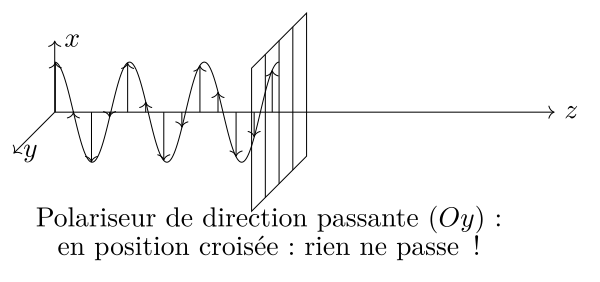
Le champ émergeant peut s’écrire $\overrightarrow{E}=E\,\cos\alpha\,\overrightarrow{u}$, où $\overrightarrow{u}$ est la direction passante du polariseur et $\alpha$ l’angle entre cette direction et la polarisation de l’onde incidente. L’intensité énergétique de l’onde étant proportionnelle au carré du champ électrique, on a en sortie de polariseur ce qui constitue la loi de Malus : $\boxed{I=I_0\,\cos^2\alpha}$

Expérience des fentes de Young

Lorsqu’une onde rencontre un obstacle de dimension proche de sa longueur d’onde (par exemple, un trou), au lieu de continuer en ligne droite, elle s’éparpille dans toutes les directions : c’est la diffraction. Ainsi, l’image d’un point est une tache de dimension angulaire typique $\lambda/\ell$, où $\ell$ est la taille de l’objet.

Lorsque deux ondes arrivent au même endroit, elles se superposent. Moyennant certaines conditions, elles peuvent s’ajouter ou s’annihiler : ce sont les interférences. On observe ainsi une succession de franges lumineuses et sombres.

L’expérience des fentes de Young mêle interférences et diffraction à travers deux fentes larges de $\ell$ et distantes de $d$ (d’un centre à l’autre centre). Il apparaît des franges d’intensité variable selon la direction d’observation $\theta$. La répartition de l’intensité à l’infini est donnée par la formule suivante : \begin{equation} I(\theta) =\frac{I_{MAX}}{2}\, \left[\frac{\sin\left(\frac{\pi\ell}{\lambda}\sin\theta\right)} {\frac{\pi\ell}{\lambda}\sin\theta}\right]^2 \,\left[1+\cos\left(\frac{2\pi\,d}{\lambda}\sin\theta\right)\right] \end{equation}

On distingue dans cette formule un terme typique de la diffraction et un terme typique des interférences. L’allure de la courbe d’intensité est la suivante :

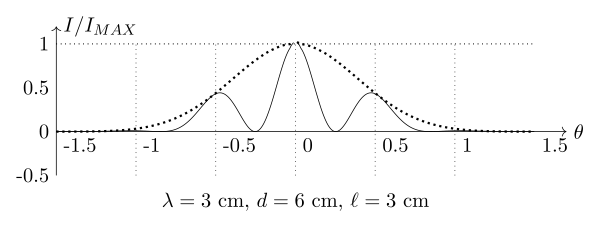
Tâches

Préparation

$\bullet$ Si on note $x_k$ la position d’un nœud d’onde stationnaire de longueur d’onde $\lambda$, quel est la distance entre deux nœuds consécutifs $x_k$ et $x_{k+1}$?

$\bullet$ Si la position des nœuds évolue selon $x_k=a\,k+b$, exprimer $x_{k+1}-x_k$.

$\bullet$ On interpose une grille métallique qui fait office de polariseur entre le cornet émetteur et le récepteur, qui mesure la tension $U$. La loi recherchée est $U=U_0\,\cos^n(\theta-\theta_0)$. Elle dérive directement de la loi de Malus du type $I=I_0\,\cos^2(\theta-\theta_0)$.
Sachant que la grille et le récepteur font chacun office d’analyseur de polarisation, quelle valeur de puissance $n$ est attendue dans la loi recherchée?

$\bullet$ On prend $\lambda=3$ cm, $\ell=2,5$ cm et $d=5$ cm. Tracer à l’aide de python la loi donnant l’intensité en fonction de $\theta$ dans le cadre de l’expérience des fentes de Young. Tracer également cette loi sans la modulation apportée par la diffraction.

$\bullet$ Trouver les deux premières valeurs de $\sin\theta$ de part et d’autre de $\theta=0$, pour lesquelles la fonction suivante s’annule et celles pour lesquelles elle est maximale : \begin{equation}1+\cos\Bigg(\frac{2\pi\,d}{\lambda}\sin\theta\Bigg)\end{equation} En déduire les valeurs numériques correspondantes de $\theta$, en degrés.

Manipulations

Ondes stationnaires (30’)

1. Placer l’émetteur à peu près 40 cm d’une plaque métallique (qui fait office de miroir).
2. Déplacer lentement l’antenne entre l’émetteur et la plaque, pour repérer la position $x_k$ d’un minimum de tension. Mesurer cette position au pied du support du récepteur (ce n’est pas la position du récepteur qui compte dans cette expérience mais l’écart entre deux positions).
3. Répéter la mesure pour au moins 5 minima consécutifs.
4. Porter les mesures dans Regressi : une colonne pour le numéro $k$ de la mesure, une colonne pour la position $x_k$.
5. Tracer la position en fonction du numéro de la mesure.
6. Si la relation semble affine, on a $x_k=a\,k+b$. En déduire la longueur d’onde $\lambda$.

Fentes de Young (45’)

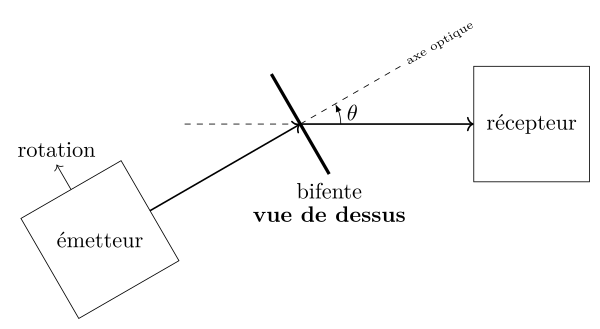
Il s’agit de reproduire l’expérience des fentes de Young dans le domaine hertzien : on intercale une bifente entre l’émetteur et le récepteur.

$\bullet$ Étude grossière : (20’)

1. Placer le cornet émetteur à peu près 40 cm de la bifente et le cornet récepteur à 70 cm. Aligner le montage. Bien orienter les cornets (qui tournent sur eux-mêmes).
2. Placer la bifente entre l’émetteur et le récepteur sur le rapporteur.
3. Positionner précisement l’émetteur en bougeant légèrement (moins de 1 cm) sa position le long de l’axe, de façon à maximiser la tension $U_{MAX}$ mesurée. Consigner cette valeur. Elle doit être inférieure à 10 V. Fixer l’émetteur à l’aide de pâte adhésive.
4. Relever directement sous regressi la tension U lorsque l’angle $\theta$ varie, en prenant des mesures tous les 5 degrés de $-40$ à $40$. Tracer grossièrement l’allure de $U/U_{MAX}$ à l’aide de regressi.
5. Attention, pour les angles élevés, il se peut que l'onde aille directement de l'émetteur au récepteur, sans passer à travers la bifente. Il peut être judicieux d'ajouter des écrans métalliques pour éviter cela.
6. Commenter l’allure de la courbe.

$\bullet$ Étude quantitative : (25’)

1. Mesurer précisement la largeur $\ell$ des fentes et la distance $d$ entre les fentes (d’un bord intérieur à un bord extérieur, pour une bonne précision, car il est difficile de pointer le centre d’une fente).
2. Repérer précisement (au degré près) les premiers minima et maxima de tension $\theta_\mathrm{min}$ et $\theta_\mathrm{max}$, situés de part et d’autre du maximum central, pour lequel $\theta\simeq 0$, en effectuant plusieurs mesures resserrées autour de ces points particuliers.

À partir des valeurs $d$, $|\theta_\mathrm{min}|$ et $|\theta_\mathrm{max}|$, en utilisant les résultats trouvés en préparation, calculer les valeurs de longueur d’onde qui correspondent accompagnées de leur incertitude.

---

Loi de Malus (45’)

Pour étudier la loi de Malus, on dispose de deux grilles : l’une est grossière, l’autre est graduée en degrés et permet des mesures.

$\bullet$ Analyse qualitative (grille grossière) : interposer une grille entre récepteur et émetteur.



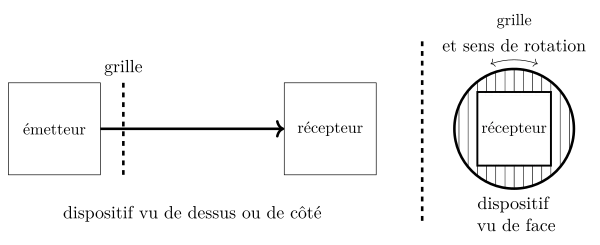
Observer ce qui se passe lorsque la grille tourne autour de sa normale. Expliquer cela.

$\bullet$ Analyse quantitative (avec grille de mesure) :

1. Placer l’émetteur à peu près 100 cm du récepteur.
2. Placer la grille de mesure accolée au cornet émetteur.
3. Positionner précisément l’émetteur en bougeant légèrement (moins de 1 cm) sa position, de façon à maximiser la tension mesurée.
4. Tourner la grille sur elle-même, $\theta$ variant de 10 en 10 et mesurer la tension. Attention, attendre la relative stabilisation de la tension avant de la mesurer. Prendre soin de s’éloigner du montage afin de ne pas le perturber. Noter l’incertitude sur la tension.
5. Enregistrer les mesures d’angle et de tension ainsi que les incertitudes de mesure.
6. Estimer la tension $U_0$ maximale ainsi que l’angle $\theta_0$ de la grille correspondant.

La loi recherchée est $U=U_0\,\cos^4(\theta-\theta_0)$.

Tracer la courbe $U/U_0$ en fonction de $\theta$.

Les valeurs mesurées sont-elles compatibles avec la relation théorique?

Matériel

$\bullet$ 1 kit onde centimétrique : émetteur avec alimentation, une antenne réceptrice ponctuelle et une antenne cornet
$\bullet$ Un écran métallique
$\bullet$ 1 voltmètre
$\bullet$ Un banc gradué dont une partie est orientable
$\bullet$ Une bi-fente métallique
$\bullet$ Une grille métallique grossière
$\bullet$ une grille métallique fine, gradué en degrés