La physique à l'ENSCR

Simulation numérique.

Ondes scalaires et vectorielles.

Ce TP de simulation numérique se déroule en trois parties:

Une partie théorique où on en apprend un peu sur les ondes vectorielles, la polarisation et l'interaction entre lumière et matière.
Une partie simulation où il s'agit de tracer l'allure d'ondes, de comprendre le rôle de la longueur d'onde, du vecteur d'onde, de l'espace, du temps et surtout de visualiser les ondes en 2D et 3D pour fixer des images en tête.
Enfin, l'utilisation d'emanim, un code python qui trace des ondes dans différentes situations.

Il vous est demandé de rendre votre travail au format pdf sur la page e-learning Physique CPI/2 ICI.
Composer avec le logiciel de son choix (libreoffice, document latex, html, etc). En plus des réponses aux questions, n'oubliez pas de rendre le code tapé et les images obtenues.

Partie théorique.

Cliquer sur le lien suivant pour accéder à la partie théorique.
Elle présente la notion d'onde polarisée rectilignement (PR) et d'onde polarisée circulairement (PC) ainsi que le résultat de la superposition de différentes ondes. Enfin, elle aborde les interactions onde/matière.

Simulons!

Dans cette partie, on utilise l'informatique et le langage de programmation python. On utilise le logiciel spyder pour copier/coller le code proposé avant de le modifier et de l'exécuter.

Une simple courbe 2D y=f(x)
Une courbe animée y=f(x,t)
Une simple courbe 3D z=f(x,y)

Il est demandé de reproduire les différentes images présentées dans le compte-rendu.

Un graphique simple

Le code python ci-dessous permet de tracer une courbe sinusoïdale. La librairie matplotlib est utilisée pour tracer des courbes.

# -*- coding: utf-8 -*-
# 202207
# une ligne qui commence par un dièse est une ligne de commentaire
# elle n'est pas exécutée par le programme

# on importe des bibliothèques, des fonctions, des constantes...
from math import sin, pi
# pour pouvoir tracer des courbes, on a besoin de 'pyplot' objet du module 'matplotlib'
from matplotlib import pyplot

# temps maximal d'affichage
# Tmax=2.0 -> nombre flottant (float)
# Tmax=2 -> nombre entier (int)
Tmax=2.0

# on définit les axes (x,y) et leurs bornes
ax = pyplot.axes(xlim=(0, Tmax), ylim=(-2, 2))

# nombre d'échantillons
NbEchantillons=100

# on définit les instants de calcul de la courbe
temps=[i*Tmax/NbEchantillons for i in range(NbEchantillons)]
#TEST: print(temps)

# période
T=0.5

# courbe
macourbe=[sin(2*pi*t/T) for t in temps]
#TEST: print(macourbe)

# on rajoute la courbe sur le graphique
ax.plot(temps,macourbe)

# on demande l'affichage
pyplot.show()

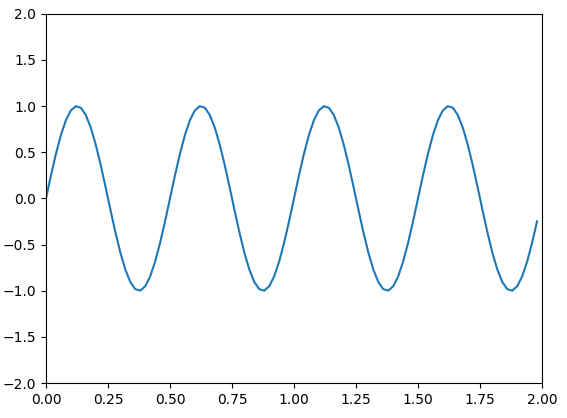
Quelle est la période de la courbe?
Tracer
```
s(t)=sin(2*pi*t/T + pi/3)
```
Tracer un cosinus.
Comment changer l'amplitude de la courbe?
Tracer
```
s(x)=2*x-3
```

Effet de sous-échantillonnage

Pour afficher une courbe, le logiciel relie des points entre eux. Plus on lui demande un grand nombre de points, plus le calcul est long. Mais attention, avec trop peu de points, on ne reproduit pas fidèlement une courbe.
L'échantillonnage consiste à découper la courbe en segments.

# -*- coding: utf-8 -*-

from math import sin, pi
from matplotlib import pyplot as plt

#temps maximal
Tmax=2.0
# définit la figure
fig = plt.figure()
#définit les axes
ax = plt.axes(xlim=(0, Tmax), ylim=(-2, 2))

#nombre d'échantillons
NbEchantillons=10
NbEchantillons2=100
temps=[i*Tmax/NbEchantillons for i in range(NbEchantillons)]
temps2=[i*Tmax/NbEchantillons2 for i in range(NbEchantillons2)]
#période
T=0.5
#TEST print(t)
macourbe=[sin(2*pi*t/T) for t in temps]
macourbe2=[sin(2*pi*t/T) for t in temps2]
#TEST print(macourbe)

ax.plot(temps,macourbe,temps2,macourbe2)
#ax.plot(temps2,macourbe2)

plt.show()

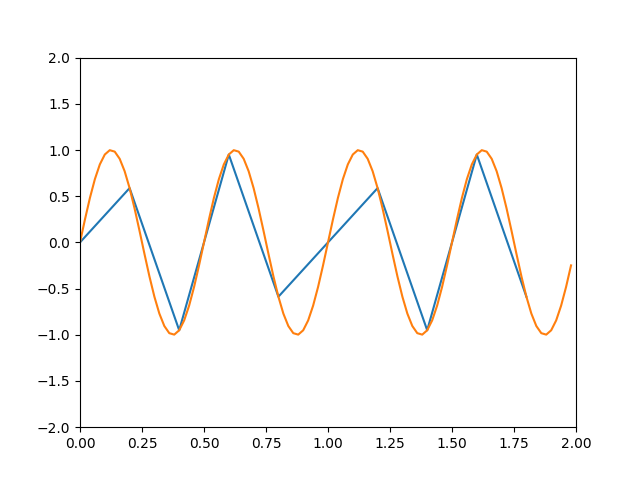
Quel est l'effet de l'échantillonnage? Modifier le nombre d'échantillons pour observer ce qui se passe.
Quel est le type de donnée de 'macourbe'? Quelle est sa longueur?
(Essayer les commandes print(type(macourbe)), type(2), type(2.0) ou type("macourbe") pour comprendre la différence)
(Pour la longueur, c'est la commande len(mescourbes) -> length)

Plusieurs courbes.

# -*- coding: utf-8 -*-
# 202207
# une ligne qui commence par un dièse est une ligne de commentaire
# elle n'est pas exécutée par le programme

# on importe des bibliothèques, des fonctions
from math import sin, pi
# pour pouvoir tracer des courbes, on a besoin de 'pyplot' objet du module 'matplotlib'
from matplotlib import pyplot

# temps final
Tmax=2.0

# on définit les axes (x,y), auxquels on rajoutera les courbes
ax = pyplot.axes(xlim=(0, Tmax), ylim=(-2, 2))

# nombre d'échantillons
NbEchantillons=100

# on définit les instants de calcul de la courbe
temps=[i*Tmax/NbEchantillons for i in range(NbEchantillons)]
#TEST: print(temps)

# période
T=0.5

# pour tracer plusieurs fois la courbe en changeant un paramètre sans tout retaper,
# on définit une fonction
def macourbe(amplitude,periode,phasedegre,t):
	return amplitude*sin(2*pi*t/periode+phasedegre*pi/180)

# courbe
mescourbes=[(macourbe(1,T,0,t),macourbe(1.5,T,30,t)) for t in temps]
#TEST: print(mescourbe)

# on rajoute la courbe sur le graphique
ax.plot(temps,mescourbes,lw=2)

# on demande l'affichage
pyplot.show()

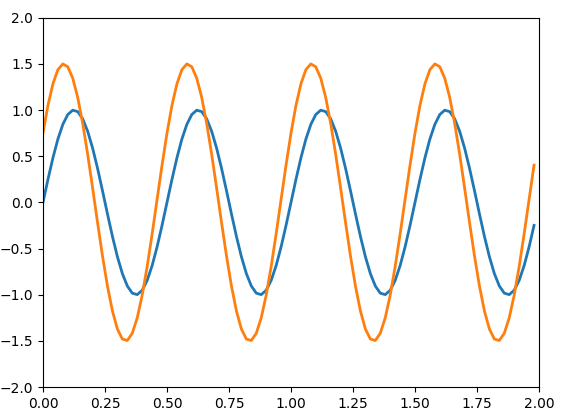
Que réalisent les lignes

def macourbe(amplitude,periode,phasedegre,t):
        return amplitude*sin(2*pi*t/periode+phasedegre*pi/180)

Quel est le type de donnée de 'mescourbes'?
Que changent les paramètres 'amplitude' et 'phasedegre'?
Comment les degrés sont-ils convertis en radian?
Réécrire le code pour que ymin et ymax soient automatiques en fonction de l'amplitude (passer cette question si elle semble trop compliquée).

onde-progressive-anim1d.py

Un peu d'animation.

Le code ci-dessous ajoute la dimension temporelle. On ne va plus tracer une courbe unique mais une suite de courbes. Attention, pour que l'affichage de l'animation fonctionne, il est nécessaire de la basculer hors de spyder; aller dans Tools > Preferences > IPython Console > Graphics > Backend et changer d'"Inline" en "Automatic".

Code python	Code cocalc
# -- coding: utf-8 -- # 202207 # on importe des bibliothèques, des fonctions from math import sin, pi # pour pouvoir tracer des courbes, on a besoin de 'pyplot' objet du module 'matplotlib' # pour pouvoir créer une animation, on a besoin de matplotlib.animation from matplotlib import pyplot, animation # échelle max selon l'axe de propagation Xmax=10.0 # échelle max selon le temps Tmax=10.0 # on définit un nom pour la figure et les axes (x,y), auxquels on rajoutera les courbes fig = pyplot.figure() ax = pyplot.axes(xlim=(0, Xmax), ylim=(-2, 2)) # nombre d'échantillons NbEchantillons=100 # on définit les positions de calcul de la courbe positionsx=[iXmax/NbEchantillons for i in range(NbEchantillons)] temps=[iTmax/NbEchantillons for i in range(NbEchantillons)] # on définit les instants de calcul de la courbe #TEST: print(temps) # période T=2.0 # vitesse c=1.0 # courbes: une liste qui contient des listes de valeurs mescourbes=[[sin(2pi/T(t-x/c)) for x in positionsx] for t in temps] # la virgule sert à unpacker courbe courbe, =ax.plot(positionsx,mescourbes[0]) def incrementemps(i): courbe.set_ydata(mescourbes[i]) return courbe, #TEST: print(mescourbes[32]) # des noms pour les axes ax.set_xlabel('X') ax.set_ylabel('Y') ax.set_title('Une onde?') # on crée l'animation line_ani = animation.FuncAnimation(fig, incrementemps, 100, interval=50, blit=False) pyplot.show()	# le code cocalc est bien plus concis que le code python: # - pas d'appel aux librairies # - nombreux raccourcis reset() #échelle max selon l'axe de propagation Xmax=10.0 # échelle max selon le temps Tmax=10.0 # nombre d'échantillons NbEchantillons=100 # on définit les instants de calcul de la courbe temps=[iTmax/NbEchantillons for i in range(NbEchantillons)] T=2 #période c=1 #vitesse # courbes: liste d'objets graphiques mescourbes=[plot(sin(2pi/T*(t-x/c)),(x,0,Xmax),ymin=-2.5,ymax=2.5) for t in temps] # animation dans cocalc monanimation=animate(mescourbes) # sauvegarde en gif # monanimation.save("onde.gif") monanimation.show()

Code python

Code cocalc

# -*- coding: utf-8 -*-
# 202207

# on importe des bibliothèques, des fonctions
from math import sin, pi
# pour pouvoir tracer des courbes, on a besoin de 'pyplot' objet du module 'matplotlib'
# pour pouvoir créer une animation, on a besoin de matplotlib.animation
from matplotlib import pyplot, animation

# échelle max selon l'axe de propagation
Xmax=10.0

# échelle max selon le temps
Tmax=10.0

# on définit un nom pour la figure et les axes (x,y), auxquels on rajoutera les courbes
fig = pyplot.figure()
ax = pyplot.axes(xlim=(0, Xmax), ylim=(-2, 2))

# nombre d'échantillons
NbEchantillons=100

# on définit les positions de calcul de la courbe
positionsx=[i*Xmax/NbEchantillons for i in range(NbEchantillons)]

temps=[i*Tmax/NbEchantillons for i in range(NbEchantillons)]
# on définit les instants de calcul de la courbe
#TEST: print(temps)

# période
T=2.0

# vitesse
c=1.0

# courbes: une liste qui contient des listes de valeurs
mescourbes=[[sin(2*pi/T*(t-x/c)) for x in positionsx] for t in temps]

# la virgule sert à unpacker courbe 
courbe, =ax.plot(positionsx,mescourbes[0])

def incrementemps(i):
	courbe.set_ydata(mescourbes[i])
	return courbe,
#TEST: print(mescourbes[32])

# des noms pour les axes
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_title('Une onde?')

# on crée l'animation
line_ani = animation.FuncAnimation(fig, incrementemps, 100, interval=50, blit=False)

pyplot.show()

# le code cocalc est bien plus concis que le code python:
# - pas d'appel aux librairies
# - nombreux raccourcis
reset()

#échelle max selon l'axe de propagation
Xmax=10.0

# échelle max selon le temps
Tmax=10.0

# nombre d'échantillons
NbEchantillons=100

# on définit les instants de calcul de la courbe
temps=[i*Tmax/NbEchantillons for i in range(NbEchantillons)]

T=2 #période
c=1 #vitesse

# courbes: liste d'objets graphiques
mescourbes=[plot(sin(2*pi/T*(t-x/c)),(x,0,Xmax),ymin=-2.5,ymax=2.5) for t in temps]

# animation dans cocalc
monanimation=animate(mescourbes)
# sauvegarde en gif
# monanimation.save("onde.gif")

monanimation.show()

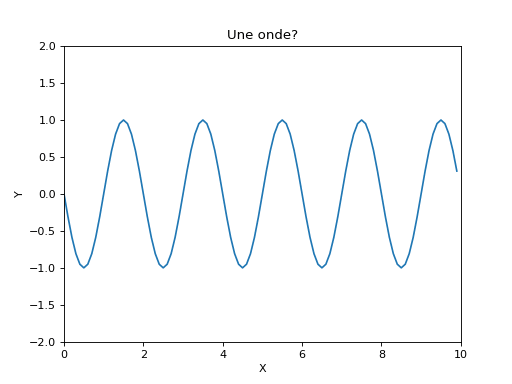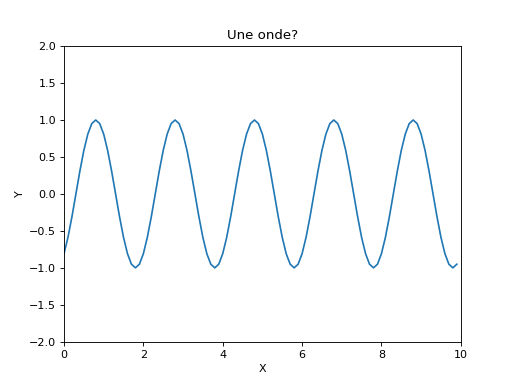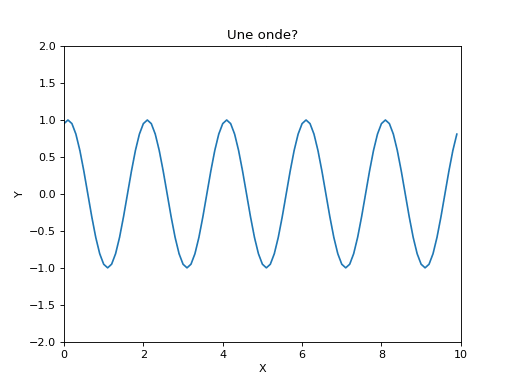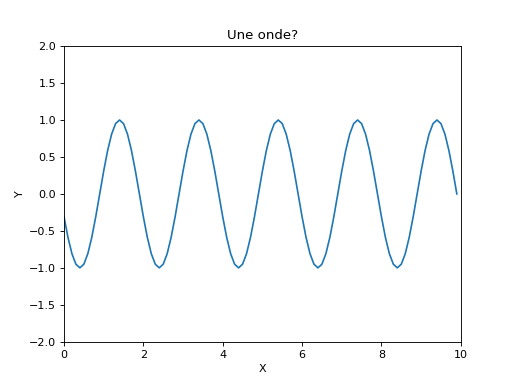
Réaliser l'animation en s'inspirant du code fourni.

Que réalise la ligne suivante? Quel est le type de variable retournée?
```
mescourbes=[[sin(2*pi/T*(t-x/c)) for x in positionsx] for t in temps]
```
Essayer de tracer une onde qui se propage en sens inverse.

Paquet d'onde.

En réalité, une onde n'est pas sinusoïdale. En particulier, elle a un début et une fin. On parle de paquet d'onde.

# -*- coding: utf-8 -*-
# 202207

#on importe des bibliothèques, des fonctions
from math import sin, exp, pi
#pour pouvoir tracer des courbes, on a besoin de 'pyplot' objet du module 'matplotlib'
#pour pouvoir créer une animation, on a besoin de matplotlib.animation
from matplotlib import pyplot, animation

#échelle max selon l'axe de propagation
Xmax=10.0

#échelle max selon le temps
Tmax=10.0

#on définit un nom pour la figure et les axes (x,y), auxquels on rajoutera les courbes
fig = pyplot.figure()
ax = pyplot.axes(xlim=(0, Xmax), ylim=(-2, 2))

#nombre d'échantillons
NbEchantillons=300
NbEchantillonsT=100

#on définit les positions de calcul de la courbe
positionsx=[i*Xmax/NbEchantillons for i in range(NbEchantillons)]

temps=[i*Tmax/NbEchantillonsT for i in range(NbEchantillonsT)]
#on définit les instants de calcul de la courbe
#TEST: print(temps)

#période
T=0.33

#vitesse
c=1

#courbes
mescourbes=[[exp(-(t-x/c)**2/1.1)*sin(2*pi/T*(t-x/c)) for x in positionsx] for t in temps]

courbe, =ax.plot(positionsx,mescourbes[0])

def incrementemps(i):
	courbe.set_ydata(mescourbes[i])
	return courbe,
#TEST: print(mescourbes[32])

## on crée l'animation
## blit=False
line_ani = animation.FuncAnimation(fig, incrementemps, 100, interval=50, blit=False)
#
pyplot.show()

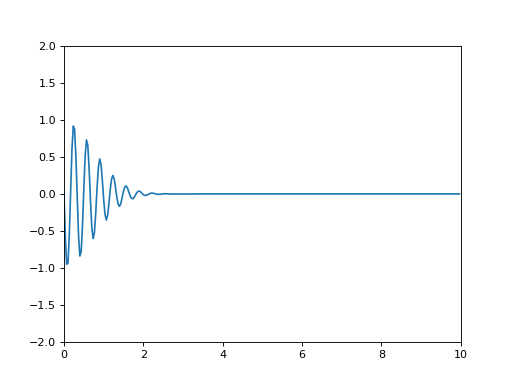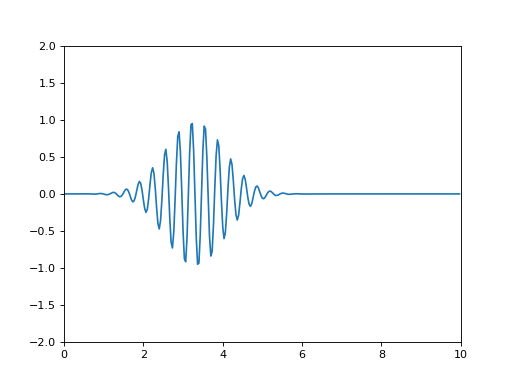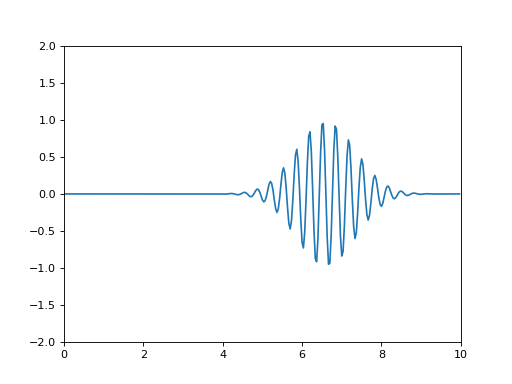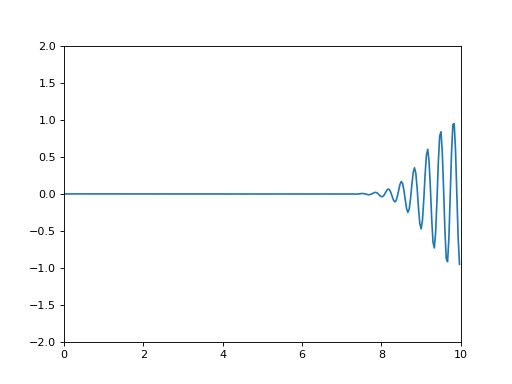
Reproduire le graphique animé ci-dessus ci-dessus en s'inspirant du code.

Onde stationnaire.

En additionnant deux ondes (une progressive et une regressive), on peut former une onde stationnaire. Ce résultat est souvent obtenu lors de la superposition d'une onde incidente et d'une onde réfléchie.

# -*- coding: utf-8 -*-
# 202207

#on importe des bibliothèques, des fonctions
from math import sin, pi
#pour pouvoir tracer des courbes, on a besoin de 'pyplot' objet du module 'matplotlib'
#pour pouvoir créer une animation, on a besoin de matplotlib.animation
from matplotlib import pyplot, animation

#échelle max selon l'axe de propagation
Xmax=10.0

#échelle max selon le temps
Tmax=10.0

#on définit un nom pour la figure et les axes (x,y), auxquels on rajoutera les courbes
fig = pyplot.figure()
ax = pyplot.axes(xlim=(0, Xmax), ylim=(-2, 2))

# nom de l'axe x
ax.set_xlabel('X')
# nom de l'axe y
ax.set_ylabel('Y')
# titre du graphique
ax.set_title('Une onde?')

#nombre d'échantillons
NbEchantillons=100

#on définit les positions de calcul de la courbe
positionsx=[i*Xmax/NbEchantillons for i in range(NbEchantillons)]

#on définit les instants de calcul de la courbe
temps=[i*Tmax/NbEchantillons for i in range(NbEchantillons)]
#TEST: print(temps)

#période
T=2

#vitesse
c=1

#toutes les courbes
mescourbes=[[sin(2*pi/T*(t-x/c))+sin(2*pi/T*(t+x/c)) for x in positionsx] for t in temps]

# initialisation: première courbe
courbe, =ax.plot(positionsx,mescourbes[0])

# pour utiliser la fonction animation, on a besoin de passer d'un graphique à un autre
# cette fonction incrémente le temps pour recréer un ensemble de valeurs y
def incrementemps(i):
	courbe.set_ydata(mescourbes[i])
	return courbe,

## on crée l'animation
## blit=False
line_ani = animation.FuncAnimation(fig, incrementemps, 100, interval=50, blit=False)

pyplot.show()

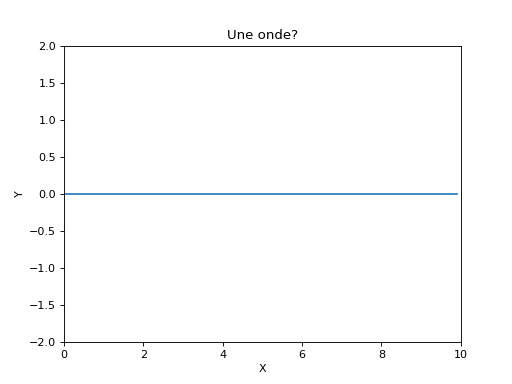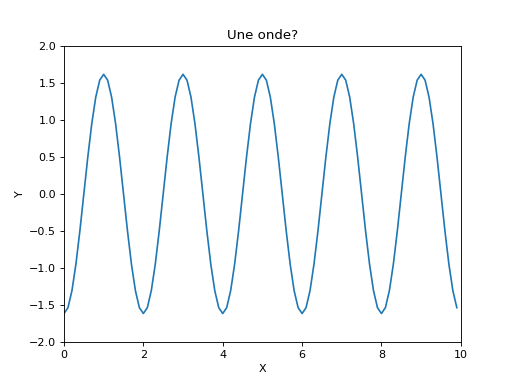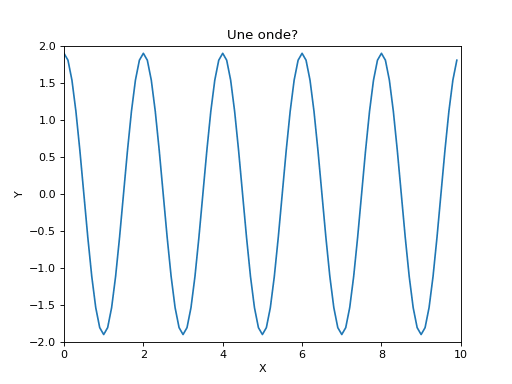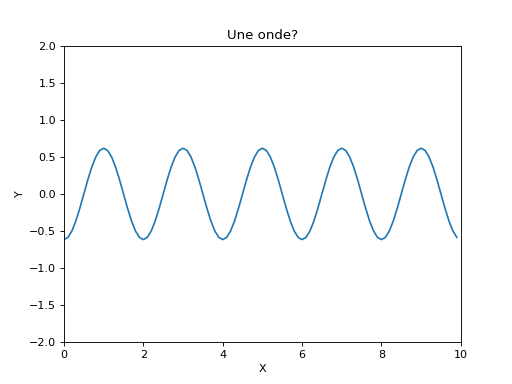
Quelle est la distance entre deux nœuds? Que peut-on en dire? Essayer de modifier le code pour modifier la distance entre deux nœuds.

Onde 3D.

Pour tracer une courbe en 3 dimensions, on doit ajouter une variable d'espace...

Code python	Code cocalc
# -- coding: utf-8 -- # O.Frantz 202207 # on importe des bibliothèques, des fonctions from math import sin, pi # pour pouvoir tracer des courbes, on a besoin de 'pyplot' objet du module 'matplotlib' from matplotlib import pyplot #max en x Xmax=10.0 # cree une figure # figaspect(1)= ratio de 1 entre les axes fig = pyplot.figure(figsize=pyplot.figaspect(1)) # on définit les axes (x,y,z), auxquels on rajoutera les courbes ax = pyplot.figure(figsize=pyplot.figaspect(1)).add_subplot(projection='3d') # proprietes des axes ax.set_xlim3d([0.0, Xmax]) ax.set_xlabel('x') #ax.set_ylim3d([-1.2, 1.2]) ax.set_ylabel('y') #ax.set_zlim3d([1.2, 1.2]) ax.set_zlabel('z') ax.set_title('3D') ax.spines['bottom'].set_position('zero') ax.spines['top'].set_position('zero') ax.spines['left'].set_color('none') ax.spines['right'].set_color('none') #nombre d'échantillons NbEchantillons=500 #on définit les endroits où la courbe est évaluée axeX=[iXmax/NbEchantillons for i in range(NbEchantillons)] #période (longueur d'onde) L=2 # une fonction pour calculer plus vite l'onde def mononde(amplitude,periode,phasedegre,x): return amplitudesin(2pix/periode+phasedegre*pi/180) # courbe: deux composantes déphasées de 90 degrés monondeY=[mononde(1,2,0,x) for x in axeX] monondeZ=[mononde(1,2,90,x) for x in axeX] # on rajoute la courbe sur le graphique ax.plot(axeX,monondeY,monondeZ) #on demande l'affichage pyplot.show()	reset() # x est la variable, l'onde se propage selon l'axe (Ox) var('x') # on définit une fonction opph opph(x,t,A,w,k,ph)=Acos(wt-k*x+ph) # l'onde 3d comporte deux composantes qui oscillent, selon Oy et Oz. onde3d=[x,opph(x,0,1,1,1,0),opph(x,0,1,1,1,pi/2)] # pour tracer en 3d parametric_plot3d(onde3d,(x,0,10))

Code python

Code cocalc

# -*- coding: utf-8 -*-
# O.Frantz 202207

# on importe des bibliothèques, des fonctions
from math import sin, pi
# pour pouvoir tracer des courbes, on a besoin de 'pyplot' objet du module 'matplotlib'
from matplotlib import pyplot

#max en x
Xmax=10.0

# cree une figure
# figaspect(1)= ratio de 1 entre les axes
fig = pyplot.figure(figsize=pyplot.figaspect(1))
# on définit les axes (x,y,z), auxquels on rajoutera les courbes
ax = pyplot.figure(figsize=pyplot.figaspect(1)).add_subplot(projection='3d')

# proprietes des axes
ax.set_xlim3d([0.0, Xmax])
ax.set_xlabel('x')
#ax.set_ylim3d([-1.2, 1.2])
ax.set_ylabel('y')
#ax.set_zlim3d([1.2, 1.2])
ax.set_zlabel('z')
ax.set_title('3D')
ax.spines['bottom'].set_position('zero')
ax.spines['top'].set_position('zero')
ax.spines['left'].set_color('none')
ax.spines['right'].set_color('none')

#nombre d'échantillons
NbEchantillons=500

#on définit les endroits où la courbe est évaluée
axeX=[i*Xmax/NbEchantillons for i in range(NbEchantillons)]

#période (longueur d'onde)
L=2

# une fonction pour calculer plus vite l'onde
def mononde(amplitude,periode,phasedegre,x):
	return amplitude*sin(2*pi*x/periode+phasedegre*pi/180)

# courbe: deux composantes déphasées de 90 degrés
monondeY=[mononde(1,2,0,x) for x in axeX]
monondeZ=[mononde(1,2,90,x) for x in axeX]

# on rajoute la courbe sur le graphique
ax.plot(axeX,monondeY,monondeZ)

#on demande l'affichage
pyplot.show()

reset()

# x est la variable, l'onde se propage selon l'axe (Ox)
var('x')

# on définit une fonction opph
opph(x,t,A,w,k,ph)=A*cos(w*t-k*x+ph)

# l'onde 3d comporte deux composantes qui oscillent, selon Oy et Oz.
onde3d=[x,opph(x,0,1,1,1,0),opph(x,0,1,1,1,pi/2)]

# pour tracer en 3d
parametric_plot3d(onde3d,(x,0,10))

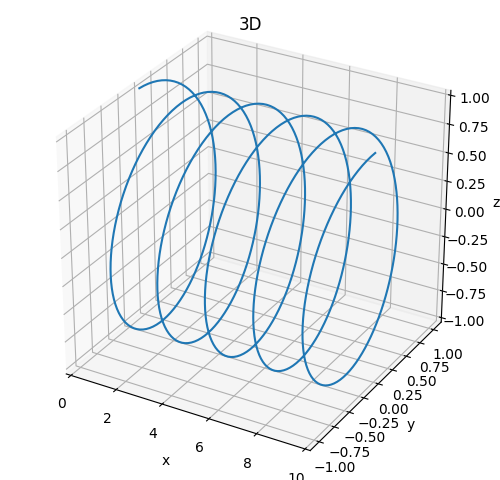
Quelle est la polarisation présentée sur la figure ci-dessus?
Modifier le code pour modifier la polarisation et ainsi obtenir une polarisation rectiligne à 45 degrés des axes.

EMANIM

Nous allons utiliser l'application emanim, code écrit en python par András Szilágyi: EMANIM. Des configurations préréglées sont accessibles via le menu 'Phénomènes" ou "Phenomenon".

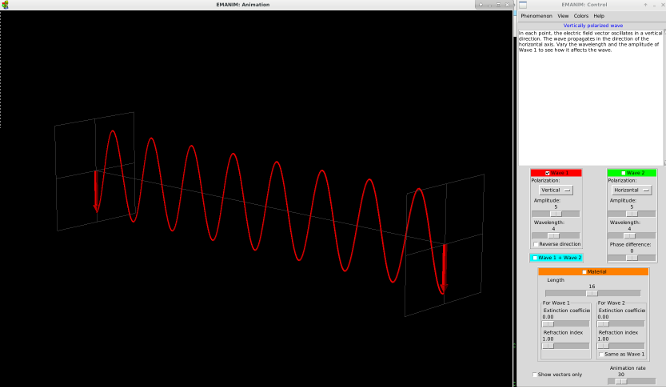
Visualiser des ondes polarisées circulairement (PC), gauche ou droite, sous différents point de vue.
Lorsque l'onde polarisée circulairement droite arrive vers l'observateur tourne-t-elle dans le sens trigonométrique ou horaire?
Additionner deux ondes rectilignes (PR) pour fabriquer une onde circulaire (PC).
Quel doit être le déphasage entre les deux ondes PR pour fabriquer une PC? L'amplitude?
En ajoutant deux ondes qui se propagent en sens contraire, on peut former une onde stationnaire. Observer les nœuds et les ventres.
On introduit un milieu réfringent transparent (par exemple, du verre, du plastique, un cristal etc) sur le chemin de l'onde. Que peut-on dire de la vitesse de l'onde dans le milieu? Que peut-on dire de sa longueur d'onde?

Dans une dernière simulation, le milieu considéré possède un pouvoir rotatoire: c'est le phénomène de biréfringence circulaire; le milieu est doté de deux indices de réfraction différents selon la polarisation circulaire gauche ou droite.
En conséquence, une onde polarisée rectilignement qui pénètre dans le milieu voit son plan de polarisation tourner!
Cette propriété est utilisée en chimie pour mesurer des concentrations car l'activité optique lui est proportionnelle. Le TP 6 de physique de 2e année propose cette manipulation.
Observer comment évoluent les différentes ondes dans le milieu.