TP-cours : circuit RLC en régime forcé - CORRECTION
En vidéo
Réalisation du montage
Montage sur PARTSIMM
Analyse fréquentielle
Simulation
Questions
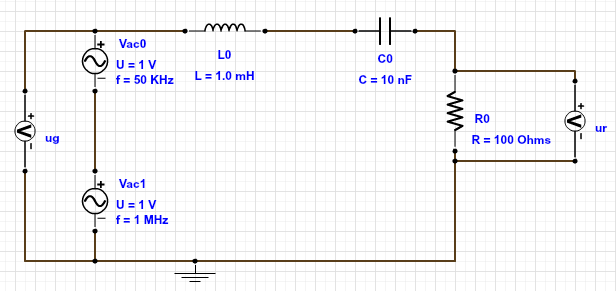
La tension aux bornes de la résistance présente un pic. On est en présence d'un filtre passe-bande.
La fréquence centrale vaut $50036\,\mathrm{Hz}$ que l'on compare à $f_0=\cfrac{1}{2\pi\sqrt{LC}} = 50329\,\mathrm{Hz}$. L'écart vient de la précision du simulateur, il faudrait encore augmenter le "output accuracy" pour plus de finesse, mais le temps de simulation serait long.
Les fréquences sont $f_2 = 58956\,\mathrm{Hz}$ et $f_1 = 42970\,\mathrm{Hz}$ ce qui donne une bande passante égale à $16000\,\mathrm{Hz}$ environ.
Le facteur de qualité vaut $Q=f_0/\Delta{f} = 3,13$ et est équivalent à sa valeur théorique $Q=\cfrac{1}{R}\sqrt{\cfrac{L}{C}} = 3,16$.
Avec une résistance deux fois moins importante, on peut trouver $\Delta\,f = 6800\,\mathrm{Hz}$. Le filtre a une bande passante plus étroite si la résistance diminue. Il est donc plus sélectif.
Analyse temporelle
Simulation
Questions
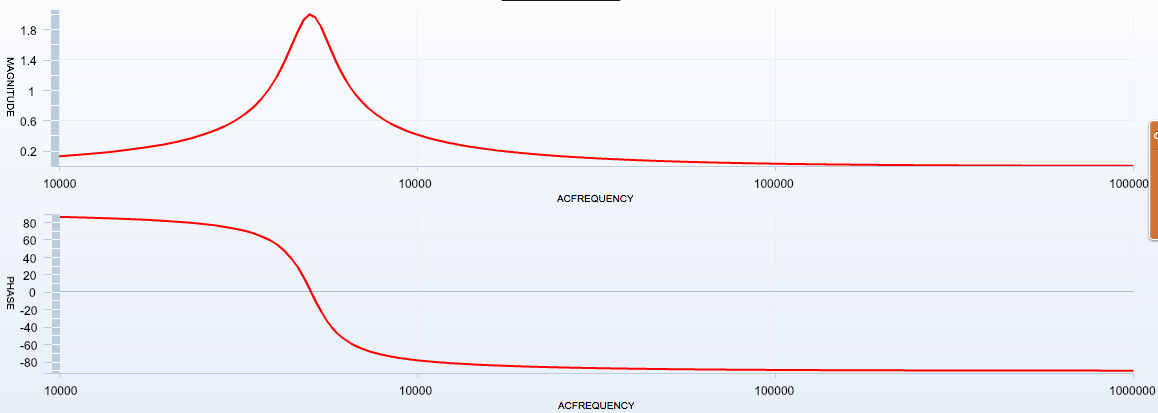
La tension d'entrée est composée de deux sinusoïdes "imbriquées" : un signale basse fréquence ($50\,\mathrm{kHz}$) "porte" un signal haute fréquence ($1\,\mathrm{MHz}$).
Nous avons vu précédemment que le circuit constitué un filtre passe-bande avec une fréquence centrale de $50\,\mathrm{kHz}$. Ainsi seul le signal de $50\,\mathrm{kHz}$ contenu dans le signal d'entrée apparaît en sortie.
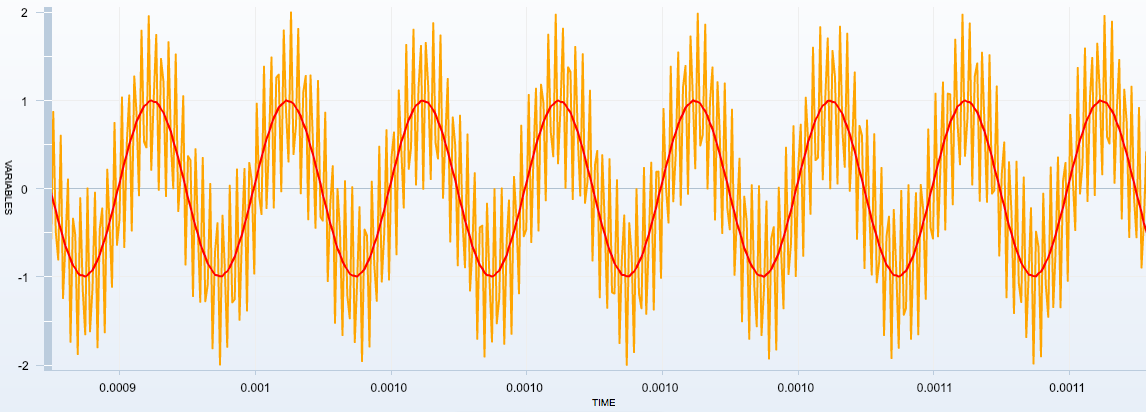
Pour récupérer le signal haute fréquence, il faut choisir une capacité de condensateur qui permet de centrer la fréquence $f_0$ du filtre passe bande sur 1 MHz. Avec $f_0=\cfrac{1}{2\pi\sqrt{LC}}$, l'inductance de la bobine étant fixée à 1 mH, on calcule C et on trouve $C = 2.5 \times 10^{-11}\,\mathrm{F} = 25\,\mathrm{pF}$.
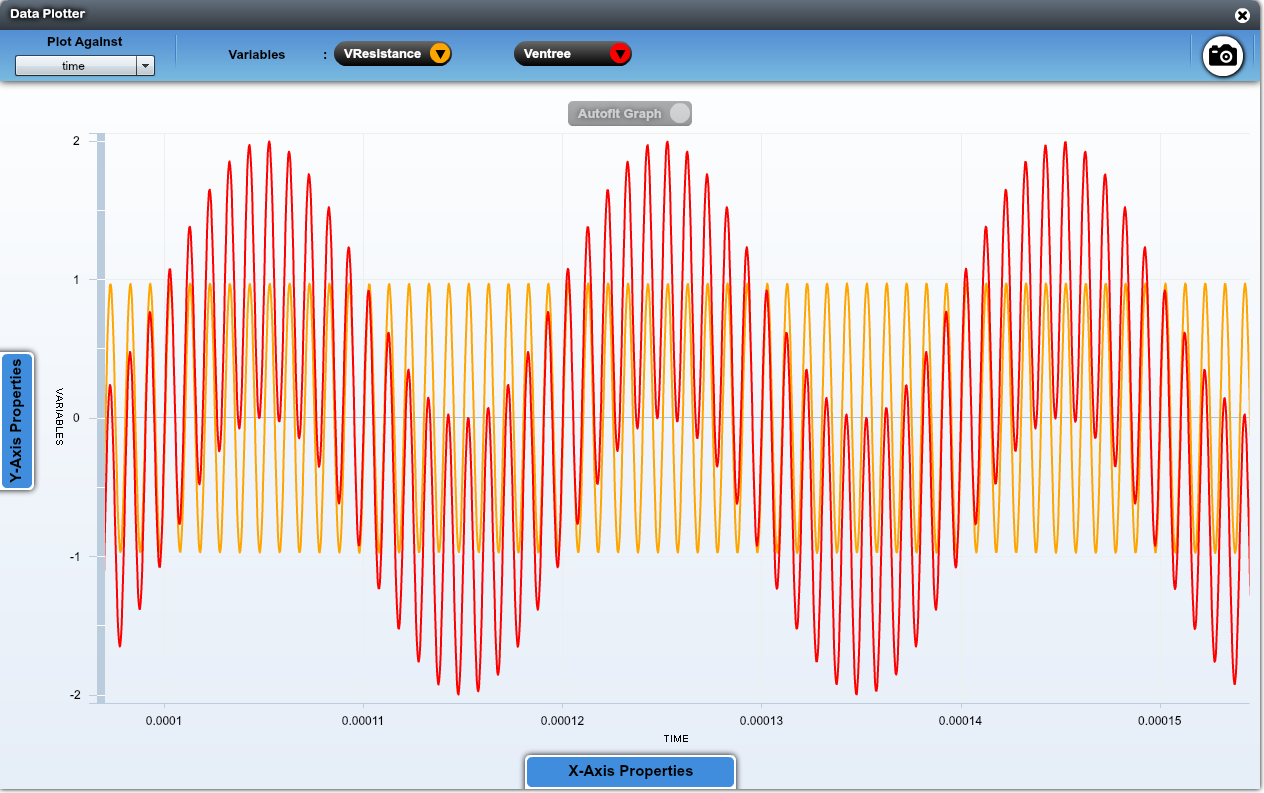
On récupère bien le signal haute fréquence car la bande passante du filtre passe-bande est centré sur $f_0 = 1$ MHz.
Exercice : filtre passe bas
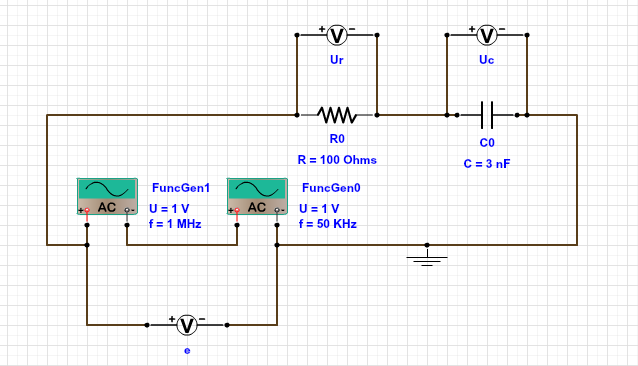
Aux bornes de la résistance, on récupère le signal haute fréquence.
Aux bornes du condensateur, on récupère le signal basse fréquence.
En effet, à haute fréquence, le condensateur se comporte comme un fil : la tension y est proche de zéro !
Le condensateur reproduit donc bien les basses fréquences.
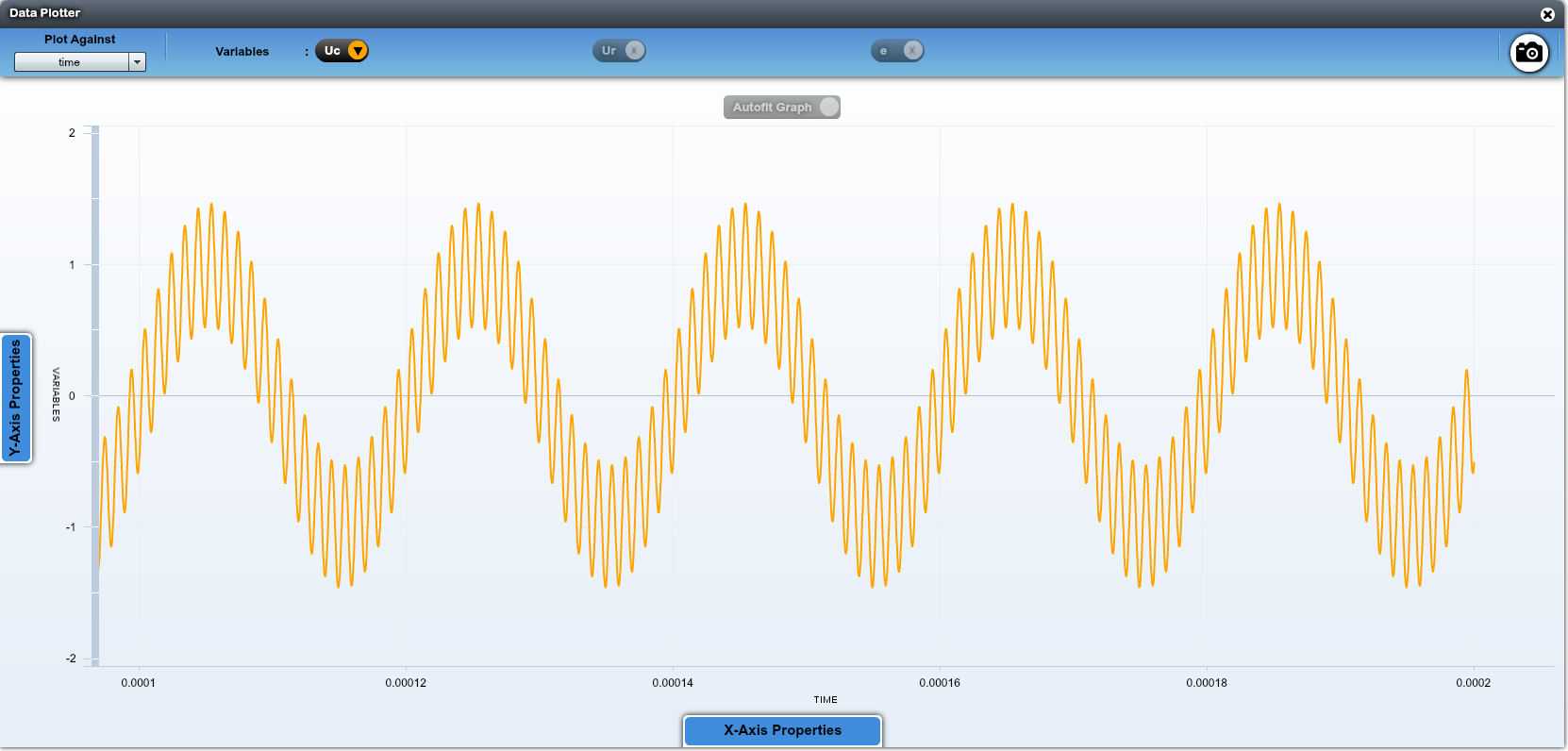
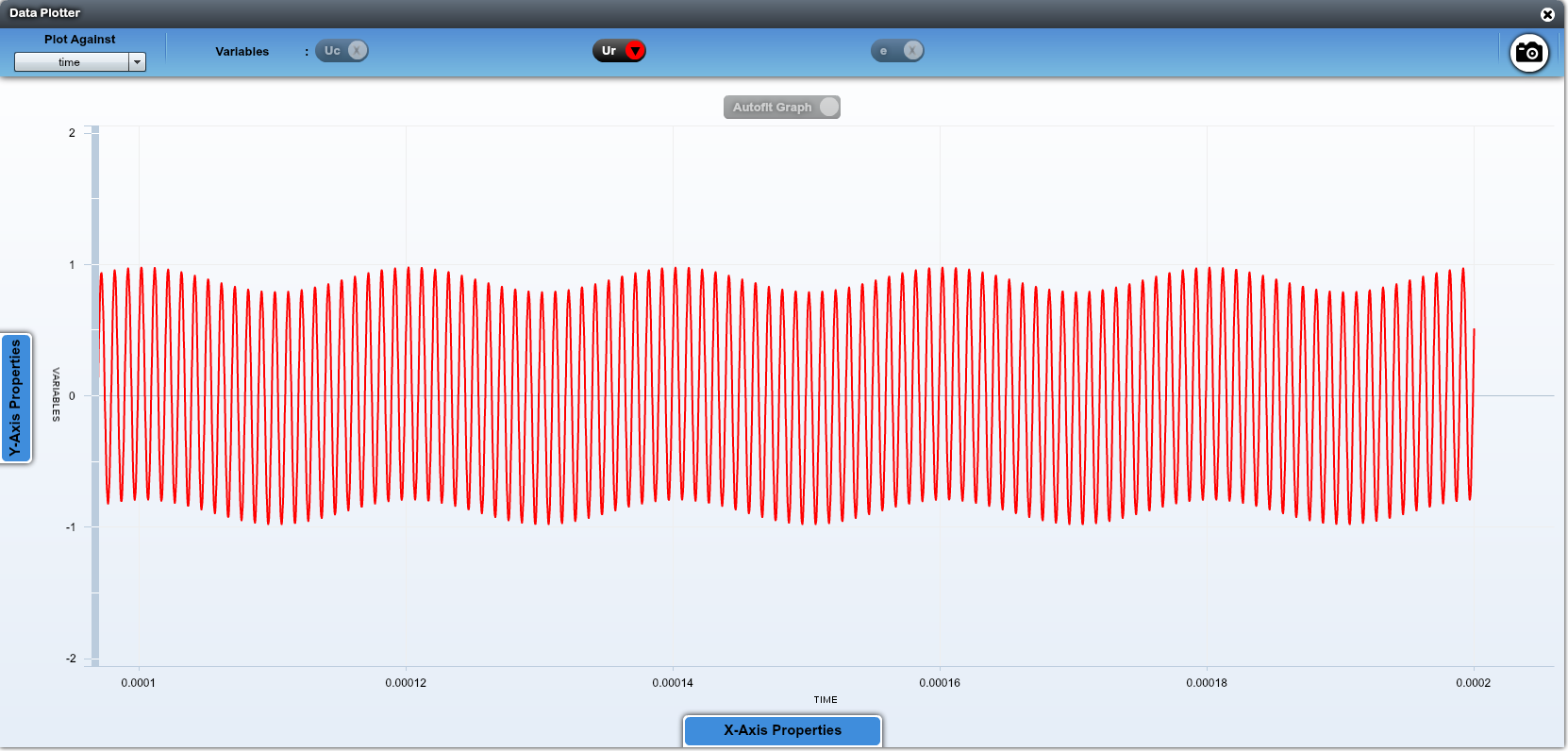
Entre 50 kHz et 1 MHz, on peut choisir une fréquence de coupure de 500MHz,ce qui conduit à $C=\dfrac{1}{2\pi\,R\,f_c}=3~\mathrm{nF}$.
Mais le résultat n'est pas parfait.
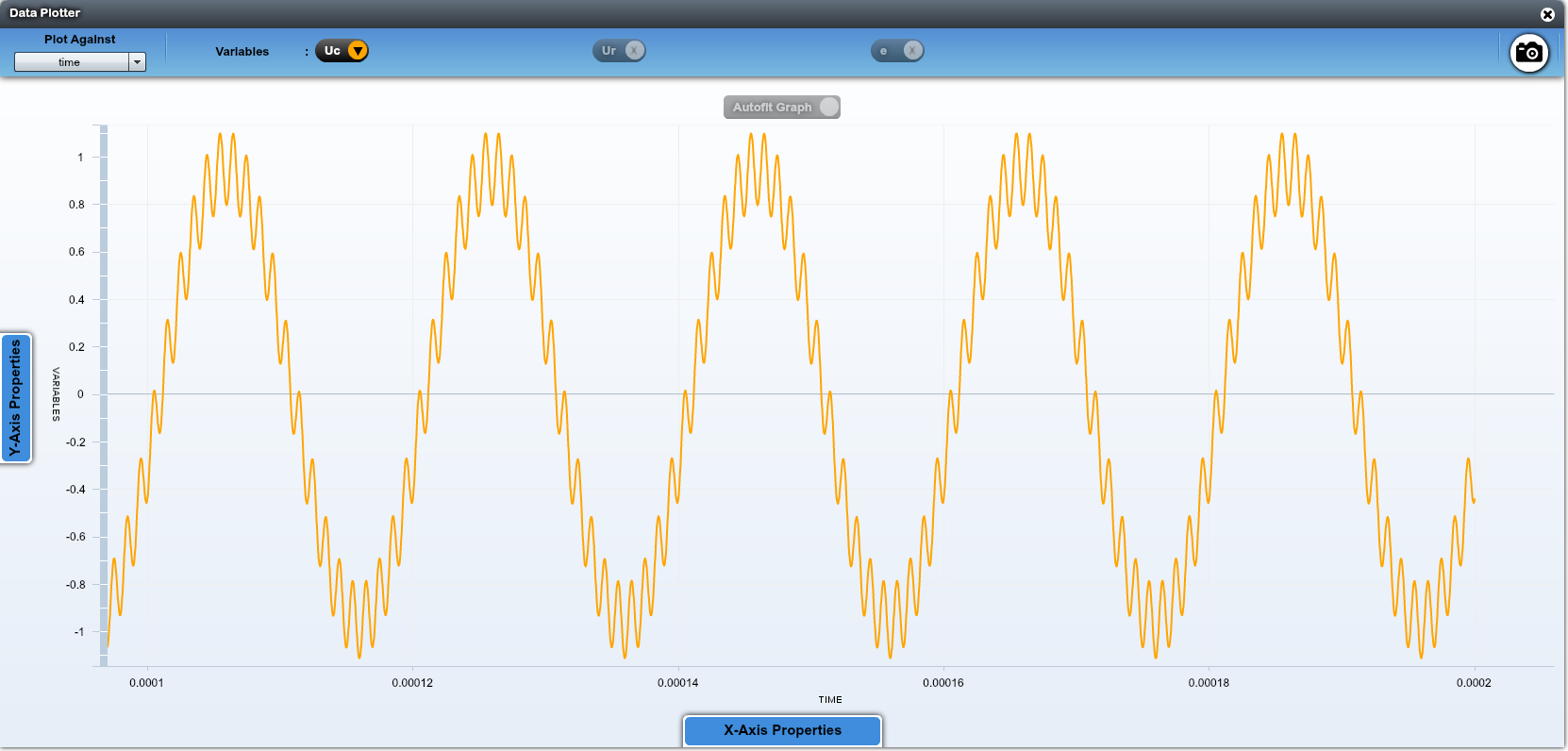
Dans $U_c$, il reste beaucoup de hautes fréquences.
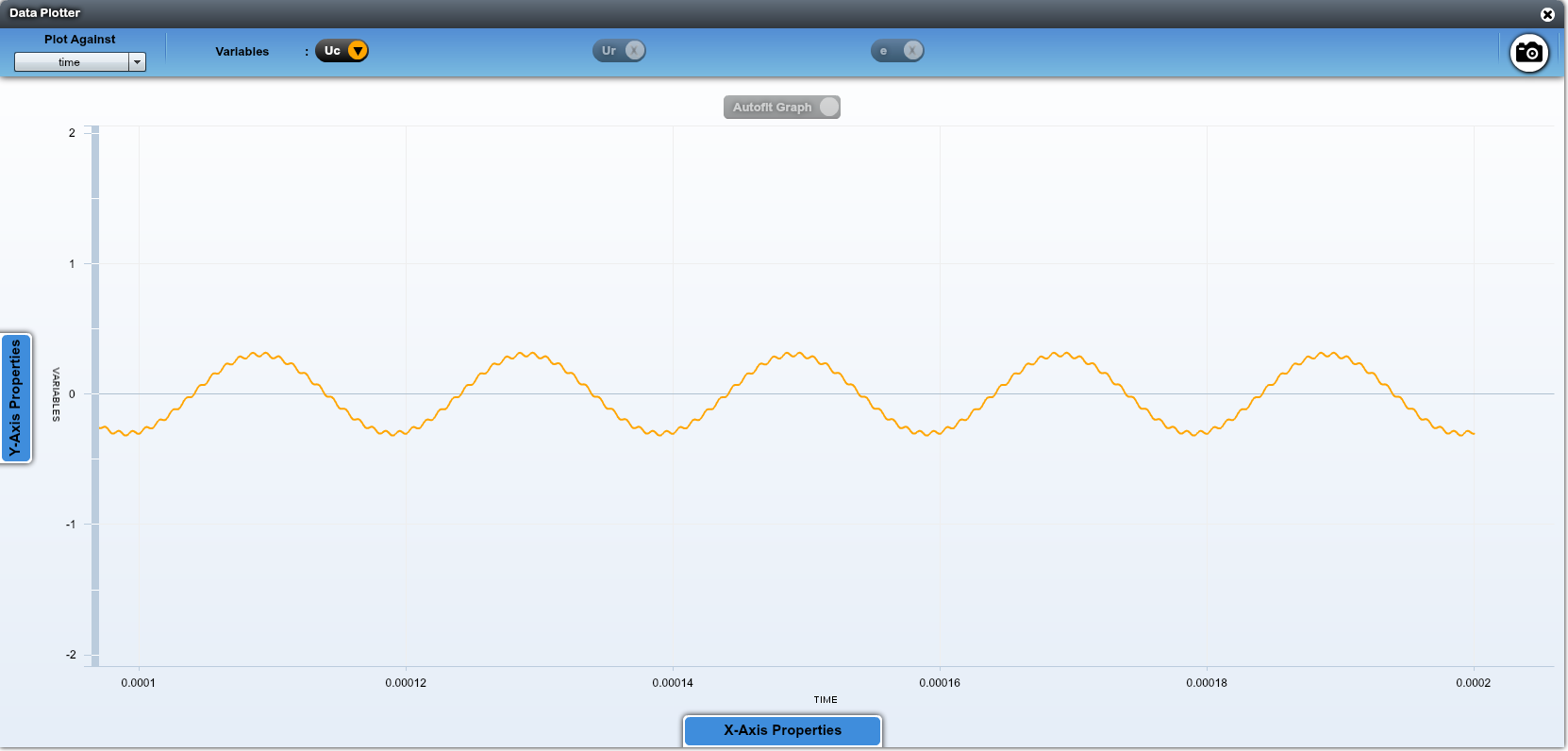
Si on augmente la valeur de la capacité, les hautes fréquences sont mieux filtrées car la fréquence de coupure diminue:
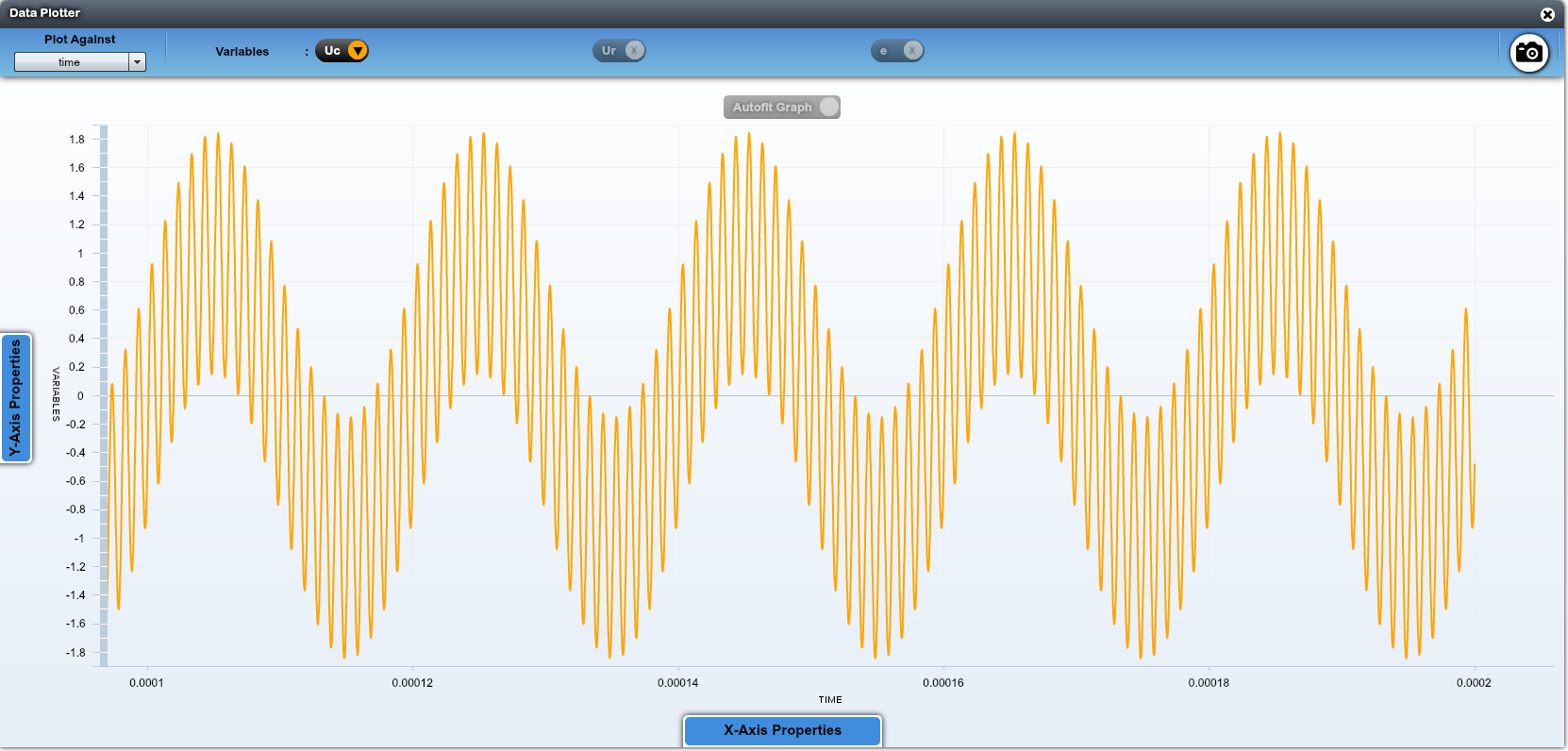

Dans $U_R$, il reste des basses fréquences. Il faut cette fois diminuer la capacité pour mieux couper les basses fréquences.
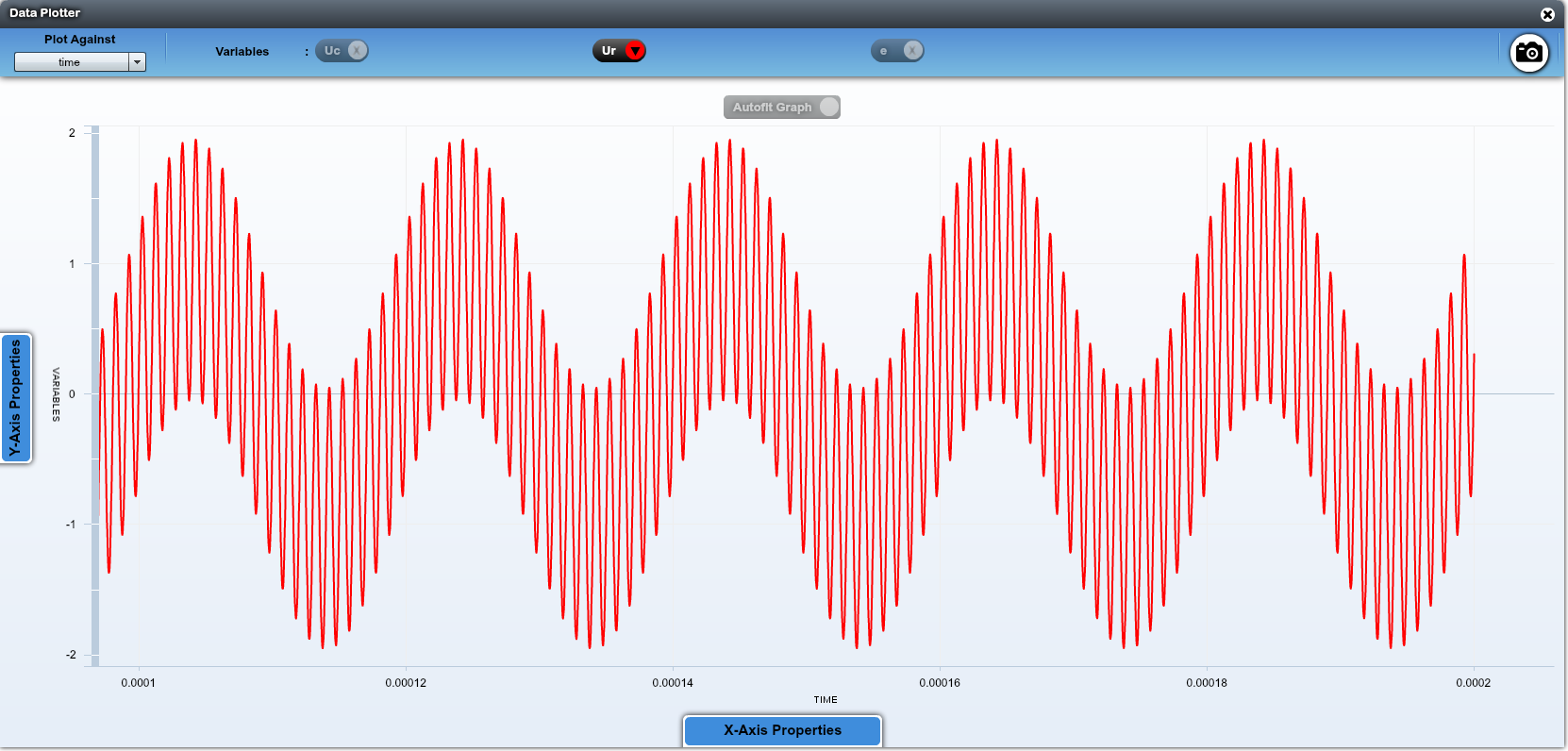


Il faut trouver un compromis si on veut avoir en même temps les basses et hautes fréquences.
10nF paraît bien, fixant la coupure à 159kHz.
$U_R=\cfrac{RC\omega}{\sqrt{1+(RC\omega)^2}}\,E$
À basse fréquence, $RC\omega\ll 1$ donc $U_R \simeq RC\omega E \to 0$. Le condensateur se comporte comme un circuit ouvert, l'intensité ne circule plus et donc la tension aux bornes de la résistance chute.
À haute fréquence, $RC\omega\gg 1$ donc $U_R \simeq E$. Le condensateur se comporte comme un fil, la tension se répercute uniquement sur la résistance: tout passe.
Le gain maximal vaut 1. Il est divisé par $\sqrt{2}$ quand $\sqrt{1+(RC\omega)^2}=\sqrt{2}$ soit $RC\omega=1$ donc $\omega_c=\dfrac{1}{RC}$
Questions-réponses
Tout d'abord dans la partie 5, je ne comprends pas trop pourquoi on choisit la fréquence de coupure de 500 kHz. C'est parce qu'il s'agit de la fréquence centrale dans le filtre passe-bande ?
Nous sommes en présence de deux filtres : si on récupère la tension aux bornes de la résistance, on a un filtre passe haut, si on récupère la tension aux bornes du condensateur, on a un filtre passe bas.
Les deux fréquences de coupure (ou pulsation sachant que $\omega = 2\pi\,f$) de ces filtres sont identiques à $\omega_C = \dfrac{1}{RC}$.
On souhaite récupérer le signal haute fréquence au niveau de la résistance et le signal basse fréquence au niveau du condensateur, on choisit donc un fréquence de coupure entre les deux signaux : entre 50 kHz et 1 MHz, on prend 500 kHz.
Ensuite, toujours dans la partie 5, je ne comprends le comportement de Ur en hautes et basses fréquences.
D'après la formule de $U_R$ : $U_R = \frac{RC \omega}{\sqrt{1+(RC\omega)^2}}E$. En basse fréquence $U_R \rightarrow 0$, la tension aux bornes de la résistance ne laisse pas passer les basses fréquences. En haute fréquence $U_R \rightarrow E$, la tension aux bornes de la résistance laisse passer les hautes fréquences.
On pourrait faire la même étude avec $U_C$ et montrer que cette tension fonctionne inversement à la tension aux bornes de la résistance.
Dans la partie 4, je ne comprends pas ce que l'on veut faire quand on dit "Calculer la valeur de capacité qui permet d'obtenir une fréquence centrale adaptée à la récupération du signal de fréquence la plus élevée uniquement. ". J'ai regardé la correction mais je n'ai pas compris.
Dans la manip précédente, on s'est servi du filtre passe-bande pour sélectionner le signal basse fréquence du signal d'entrée : on a donc choisi une $f_0$ de 50 kHz pour la fréquence centrale du filtre. On demande cette fois-ci de sélectionner la haute fréquence. Pour cela il faut changer la fréquence centrale $f_0$ du filtre en changeant, par exemple, la capacité du condensateur. Donc on effectue : $C = \frac{1}{4\pi^2\,L\,f_0^2}$.


