TP : dipôles passifs
Objectif : se familiariser avec le condensateur et les filtres électriques.
Le matériel est disponible dans le placard situé sous la paillasse, sortez ce qu'il vous faut pour le TP :
Le condensateur
Généralités
Le condensateur est un composant très fréquent dans les circuits électroniques, il peut jouer beaucoup de rôles différents. Il est composé de deux armatures métalliques séparées par un isolant, mais ces formes et types peuvent être variées.
Quand on relie un condensateur à un générateur, le courant qui circule vers le condensateur permet de charger progressivement les armatures avec des charges opposées $+q$ et $-q$.
Une fois qu'elles sont saturées de charges, le courant ne circule plus, mais une tension $U$ est mesurable entre les deux bornes du condensateur.
Une loi simple relie la charge de l'armature positive et la tension aux bornes du condensateur chargé: \begin{equation} q = C \times U \end{equation} avec $q$ la charge de l'armature positive en coulomb (C), U la tension aux bornes du condensateur en volt (V) et $C$ la capacité du condensateur en farad (F).
Théorie : charge et décharge d’un condensateur
Charge
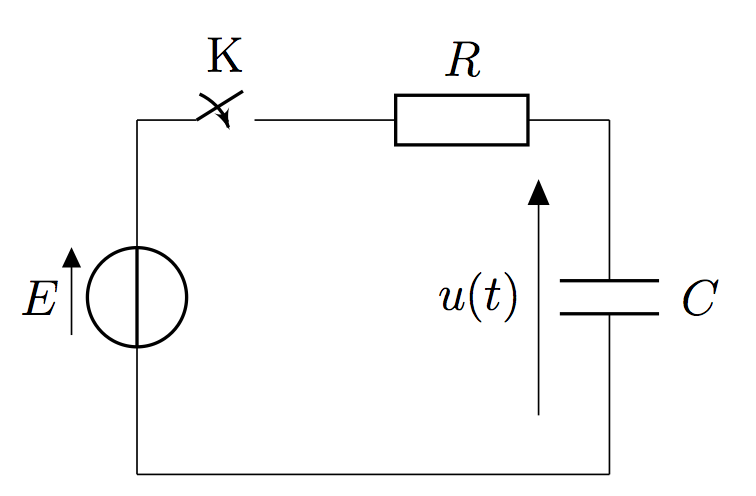
Considérons le circuit de la figure 1. Fermons l’interrupteur et appliquons la loi des mailles:
\begin{equation} E = U_R + u_C \Longrightarrow E = R\,i + u_C \Longrightarrow E = R\,C\,\dfrac{\mathrm{d}u_C}{\mathrm{d}t} + u_C \end{equation}
L'équation différentielle qui régit la charge du condensateur sous la tension $E$ est donc :
\begin{equation} \dfrac{\mathrm{d}u_C}{\mathrm{d}t} + \dfrac{u_C}{RC} = \dfrac{E}{RC} \end{equation}
Ainsi lorsque condensateur se charge sous la tension \(E\). La tension à ses bornes est donnée par la relation :\begin{equation*}\boxed{u_C(t) = E \left(1-e^{-\dfrac{t}{\tau}}\right)}\end{equation*} avec \(\tau = RC\), la constante de temps du circuit.
A préparer : montrer que pour \(t= \tau\), la tension aux bornes du condensateur a atteint 63% de sa valeur maximale.
Décharge
Si le condensateur, précédemment chargé sous la différence de potentiel \(E\), se décharge maintenant dans une résistance \(R\) ; la tension à ses bornes est de la forme :
\begin{equation*}\boxed{u_C(t) = E\,e^{-\dfrac{t}{\tau}}}\end{equation*}
Ceci est la solution de l'équation différentielle: \begin{equation} \dfrac{\mathrm{d}u_C}{\mathrm{d}t} + \dfrac{u_C}{RC} = 0 \end{equation}
Alors pour \(t = \tau\), \(u = 0,37\,E\).
Attention ! Un GBF possède une résistance interne de \(50\,\mathrm{\Omega}\), dans un circuit (en série), celle-ci vient s'ajouter aux résistances des autres composants du circuit.
Manipulation
On utilise une platine avant des composants enfichables : les 4 plots d'un ensemble sont reliés électriquement.
Pour des constantes de temps faibles, inférieures à 1 seconde, l’observation de la charge et de la décharge est possible à l’oscilloscope.
- \(\spadesuit\) Noter les valeurs de \(R\) et \(C\) puis calculer alors la constante de temps théorique \(\tau_{\mathrm{th}} = RC\) (prendre en compte le résistance interne du GBF).
Calculer l'incertitude sur cette valeur sachant que la précision constructeur sur chaque composant est de 1% de la valeur des composants. - Réaliser le montage ci-dessous :
Etude expérimentale du condensateur
Les voies 1 et 2 représentent les branchements de l'oscilloscope. Pour apprendre à faire correctement ce type de montage électrique, visionnez la vidéo suivante : - Choisir une fréquence pour que la charge et la décharge soient atteintes : \(T\), la période du créneau, doit être assez grande, mais pas trop importante afin que les mesures puissent être correctement menées (charge et décharge suffisamment dilatées) \(\Rightarrow f\simeq \dfrac{1}{10\tau}\)
- Visualiser les tensions d'entrée et de sortie sur l’oscilloscope en position DC.
- \(\spadesuit\) Utiliser convenablement cet oscillogramme (en justifiant) avec une des relations vues dans la partie théorique "charge et décharge du condensateur" pour déterminer une valeur expérimentale \(\tau_{\mathrm{exp}}\) de la constante de temps.
On utilisera les curseurs suiveurs : il est possible de les déplacer le long des courbes et d'obtenir l'abscisse et l'ordonnée de leur position, et même la différence de leurs abscisses et la différence de leurs ordonnées.
Dilatez convenablement vos échelles pour bien voir la partie du phénomène qui permet la mesure.
Estimer l'incertitude sur cette mesure.
\(\spadesuit\) Comparer la valeur expérimentale à la valeur théorique en tenant compte des incertitudes.
Attention, la vidéo ci-dessus montre la réalisation d'un montage électrique, qui n'est pas celui que vous étudiez ici !
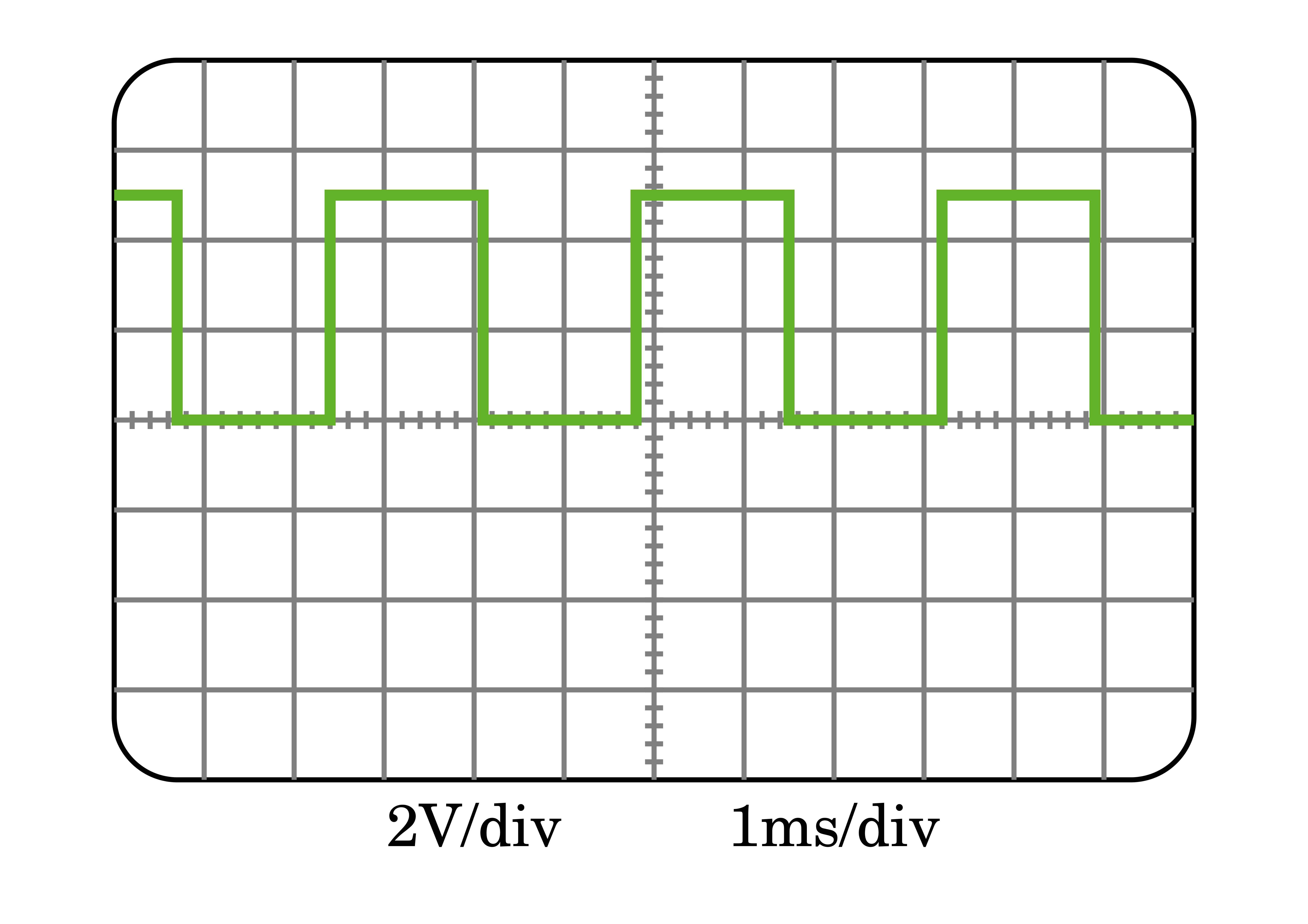
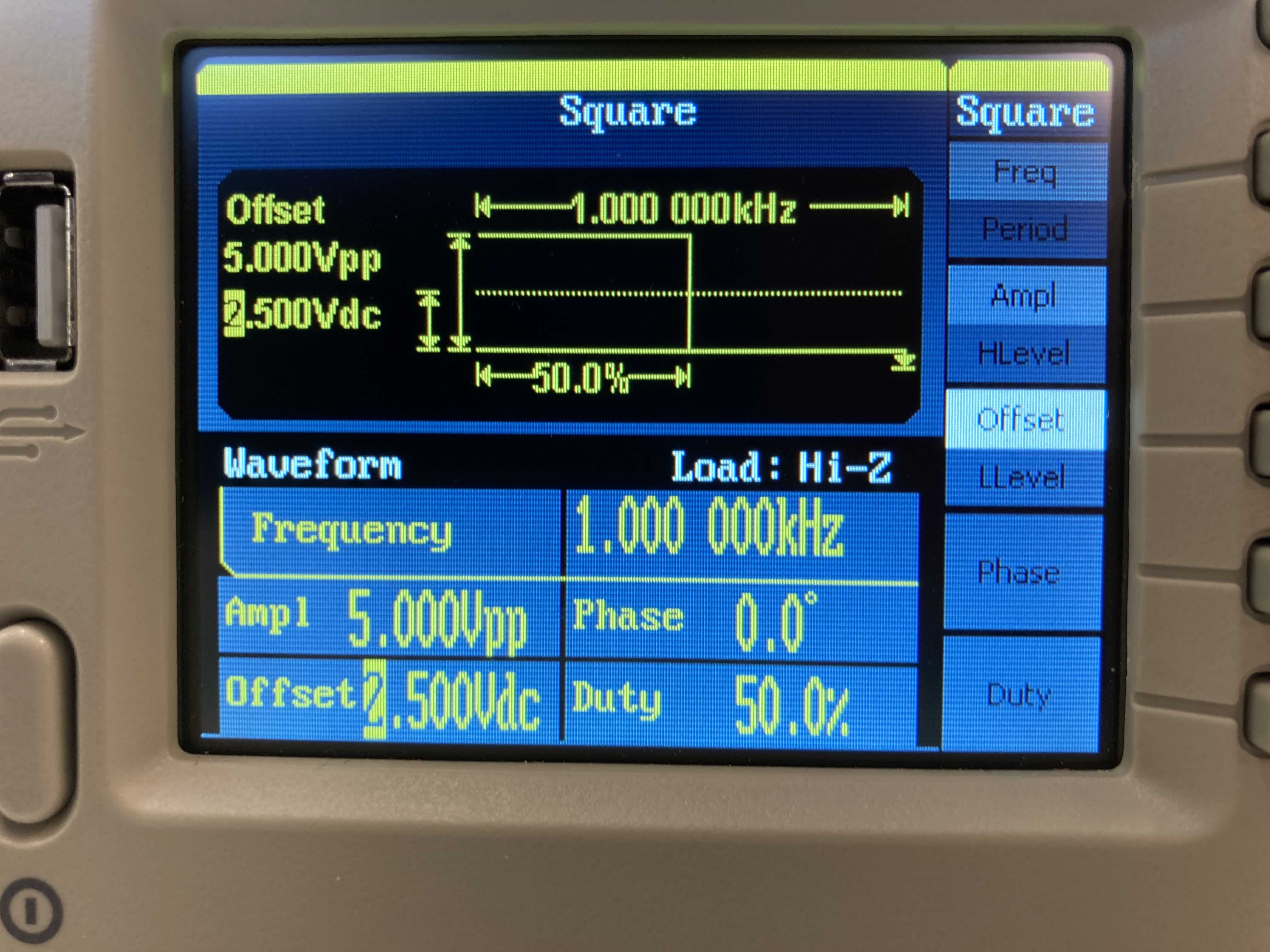
Régler le GBF pour qu'il délivre une tension entre 0 et 5V (donc ce signal a une composante continue, appelé offset, de 2,5 V). Ne pas oublier d'appuyer sur le bouton OUTPUT pour que le signal soit délivré.Association résistance-condensateur : filtre électrique
Si on impose au circuit précédent un régime sinusoïdal, c'est à dire quand le générateur délivre une signal d'entrée sinusoïdal, l'association d'une résistance et d'un condensateur devient un filtre électrique : le signal de sortie, aux bornes du condensateur, reste sinusoïdal, mais avec des caractéristiques modifiées, notamment sa phase (déphasage par rapport au signal d'entrée) et son amplitude.
Nous nous proposons d'étudier un type de filtre dans cette manipulation.
Courbes et méthodes de mesures
Dans cette manipulation, nous allons tracer deux courbes caractéristiques d'un filtre :
- La courbe de gain en fonction de la fréquence : \(G = f(f)\) où \(G =\dfrac{V_s}{V_e}\) avec \(V_s\) l'amplitude du signal de sortie et \(V_e\) l'amplitude du signal d'entrée ;
- La courbe de la tangente du déphasage en fonction de la fréquence : \(\tan\phi = f(f)\) où \(\phi\) est le déphasage de la tension de sortie sur la tension d'entrée.
On travaillera sur des fréquences allant de \(f=20\,\mathrm{Hz}\) à \(f=10\,\mathrm{kHz}\).
La première courbe sera représentée sur un axe des abscisses logarithmique (à paramétrer dans Regressi), la deuxième avec un axe linéaire.
On réalisera une dizaine de mesures du couple gain-phase.
Mesure de la fréquence
Celle-ci sera lue directement sur le GBF qui impose la tension d’entrée au filtre. Vu la stabilité du GBF utilisé, on considèrera l'incertitude nulle sur la fréquence.
Mesure du déphasage
Qu’est-ce qu’un déphasage ?
Le déphasage est une notion que l’on ne rencontre pas seulement en électricité :
Par exemple dans l’étude d’un oscillateur comme le pendule simple, on remarque que la vitesse et l’amplitude sont déphasées de 90$^\circ$ (\(\pi/2\)) : cela signifie que lorsque l’amplitude des oscillations est maximum, la vitesse est nulle, que lorsque la vitesse est maximum, l’amplitude est nulle.
Ainsi, si on trace sur un graphique la courbe de vitesse et d’amplitude en fonction du temps, on obtient la figure ci-contre.
Dans ce cas, on dit même que l’amplitude est en avance (déphasage positif) de phase de +\(\pi/2\) par rapport à la vitesse, le pic de la courbe d’amplitude est à gauche de celui de la courbe de vitesse.
Voici ce que l'on obtiendrait si les deux courbes étaient déphasées de 0 ou de $\pi$ :
Attention, ici, on parle de valeurs particulières de déphasage, mais celui-ci peut prendre n’importe quelle valeur entre \(-\pi\) et \(\pi\). D’autre part, précisons qu’un déphasage se mesure entre deux signaux synchrones, c’est à dire de même fréquence.
L’oscilloscope possède une mesure automatique de déphasage. La chercher dans le menu "measure" > "temps" de l'oscilloscope :
- Choisir la mesure de phase de la voie CH2, par exemple, (sur l'oscilloscope numérique, il y a deux types de phases pour la voie 2, choisir l'une ou l'autre car la valeur donnée est identique dans le cas de notre circuit).
- Rappelons ici que le déphasage varie entre \(-\pi\) et \(\pi\) (\(-180^{\circ}\) et \(180^{\circ}\)), si l’oscilloscope indique un déphasage supérieur à \(|180|^{\circ}\), le véritable déphasage à noter est égal à \(360^{\circ}-\phi \).
Notion de retard de phase : si le signal de sortie est en retard par rapport à l'entrée, alors le déphasage que l'on souhaite mesuré \(\phi_{s/e}\) est négatif.
Pour une bonne mesure, il faut que les signaux soient bien visibles à l’écran, utiliser tout l’écran verticalement (régler la sensibilité verticale des deux voies) et régler la base de temps afin d’observer plusieurs périodes à l’écran.
On évaluera l'incertitude sur cette mesure de déphasage.
Mesure du gain en tension
Nous allons tracer l’évolution du gain en tension en fonction de la fréquence. Il nous faut donc les amplitudes des deux voies afin de calculer \(G=\dfrac{V_\mathrm{s}}{V_\mathrm{e}}\).
Pour plus de précision, on préfèrera relever les tensions crête à crête sur chaque voie (\(V_\mathrm{pp}\)) et on pourra effectuer le rapport de ces deux tensions. En effet, \(G=\dfrac{V_\mathrm{s}}{V_\mathrm{e}} = \dfrac{2V_\mathrm{s}}{2V_\mathrm{e}} = \dfrac{V_\mathrm{spp}}{V_\mathrm{epp}}\).
Une nouvelle fois on optimisera les signaux à l’écran en réglant la sensibilité verticale des voies avant les mesures de \(V_\mathrm{epp}\) et \(V_\mathrm{epp}\) obtenues automatiquement.
On évaluera l'incertitude sur ces mesures automatiques.
Étalement des mesures
Pour réaliser de bonnes courbes, il faut choisir où prendre les mesures (à quelles fréquences).
Dans ce TP :
Pour la courbe de tension, l’échelle de fréquence en abscisse sera logarithmique : il ne faut donc pas espacer vos prises de mesures de manière régulière comme on a l’habitude de le faire (ne pas prendre des mesures tous les 500 Hz par exemple) ;
Type de filtres et fréquence de coupure
En électrocinétique, on rencontre généralement trois types de filtres que l'on reconnaît par exemple grâce à la courbe \(G=f(f)\):
- Filtre passe-bas : il laisse passer les basses fréquences (en deçà d'une certaine fréquence appelée fréquence de coupure), son gain est donc grand pour les fréquences faibles et petit pour les grandes fréquences.
- Filtre passe-haut : il laisse passer les hautes fréquences (au delà d'une certaine fréquence appelée fréquence de coupure), son gain est donc petit pour les fréquences faibles et grand pour les grandes fréquences.
- Filtre passe-bande : il laisse passer une bande de fréquence (entre deux fréquences caractéristiques appelées fréquences de coupure), son gain est donc grand dans cette bande de fréquence et faible en dehors de celle-ci.
Manipulations
On utilise toujours la platine et les composants de la manipulation précédente.
Réalisation du montage
Le montage est aussi le même que le montage précédent (voir figure 5). La seule différence est qu'ici nous injectons au montage un signal sinusoïdal.
Mesures du gain en tension et du déphasage de \(v_\mathrm{s}(t)\) par rapport à \(v_\mathrm{e}(t)\)
- Brancher le GBF sur sa sortie OUTPUT. Le régler de façon à ce qu’il délivre une tension \(v_\mathrm{e}(t)\) sinusoïdale d’amplitude 6V (Tension crête-crête égale à 12V). Régler sa fréquence à \(500\,\mathrm{Hz}\).
- Régler l’oscilloscope afin d’observer correctement les signaux \(v_\mathrm{e}(t)\) et \(v_\mathrm{s}(t)\) des deux voies (on peut dans un premier temps utiliser le bouton Autoset)
- Dans un premier temps, on cherche à connaître globalement l'évolution des signaux sur une grande gamme de fréquences. Partir d’une fréquence basse puis l’augmenter progressivement jusqu’à \(\simeq\,10\, \mathrm{kHz}\) tout en observant l’évolution des signaux à l’écran de l’oscilloscope :
- Observer l’évolution des amplitudes de \(v_\mathrm{e}(t)\) et \(v_\mathrm{s}(t)\) ;
- Observer l’évolution du déphasage de \(v_\mathrm{s}(t)\) par rapport à \(v_\mathrm{e}(t)\) (on sait théoriquement que celui-ci varie entre \(0^{\circ}\) et \(\mathbf{-90^{\circ}}\)).
- \(\spadesuit\) Pour des fréquences allant de \(\simeq\,25\,\mathrm{Hz}\) à \(\simeq\,10\,\mathrm{kHz}\), effectuer une dizaine de mesures de \(V_\mathrm{e\,pp}\), \(V_\mathrm{s\,pp}\).
Pour la mesure du déphasage \(\phi\), on prendra plutôt une dizaine de mesures sur l'intervalle \(25\,\mathrm{Hz}\) - \(2\,\mathrm{kHz}\).
Remplir deux tableaux de mesures (sous Regressi) faisant apparaître \(f\), \(V_\mathrm{epp}\), \(V_\mathrm{spp}\) d'une part et \(f\) et \(\phi\) d'autre part. Ne pas oublier les incertitudes de mesures à 68%.
Remarque - \(\spadesuit\) Compléter le tableau sous Regressi en ajoutant une ligne permettant le calcul du gain en tension \(G\).
Avec l'oscilloscope numérique, on peut faire apparaître toutes les grandeurs à mesurer en une seule fois.
Exploitation
- Tracer sous Regressi le graphique représentant le gain en tension en fonction de la fréquence avec une échelle logarithmique : pour cela, aller dans Graphe > Coordonnées puis dans "Graduations" de l’axe des abscisses choisir "log" pour logarithmique.
- Modéliser cette courbe : cliquez sur "Modèles" puis "Autres", allez dans l'onglet "Filtres" et choisissez le type de filtre approprié.
- \(\spadesuit\) Déduire de la modélisation la fréquence de coupure \(f_0\) de ce filtre ainsi que son incertitude à 95% (donnée par Regressi).
- \(\spadesuit\) Comparer \(f_0\) à la fréquence propre du filtre définie par \(f_{\mathrm{0,th}} = \dfrac{1}{2\pi RC}\). Calculer l’incertitude sur cette fréquence \(f_{\mathrm{0,th}}\) sachant que les tolérances constructeur sur les composants sont de \(1\%\).
Dans ce calcul, on ne prend pas en compte la résistance interne du GBF, car l'influence de celle-ci est prise en compte dans la mesure de \(V_\mathrm{epp}\). - Créer une nouvelle grandeur calculée \(\tan(\phi)\).
- Tracer \(\tan(\phi) = f(f)\) avec une échelle linéaire en fréquence.
- Théoriquement on a :
\(\tan(\phi) = - \frac{f}{f_0}\)
Modéliser la courbe afin d'obtenir la valeur de \(f_0\) et son incertitude à 95%. - Comparer cette valeur à celle trouvée précédemment et à la valeur théorique.
Fiche de résultats
Rendez-vous sur votre espace LabNbook pour transmettre vos résultats.
Annexe : Liste de matériel
- Un multimètre
- Un GBF Siglent SDG 810;
- Une plaque pour composants enfichables
- Un condensateur dans un module enfichable
- Un conducteur ohmique dans un module enfichable
- Un oscilloscope numérique Rigol
- Un ordinateur muni de Regressi