TP œil et lunette astronomique

Objectifs : Modéliser un œil sur un banc d'optique, être capable de "fabriquer" une lunette astronomique

Description de l’œil (cliquez pour déplier)

L’œil est l’organe de la vision ; il peut observer directement des objets ou bien examiner les images données par des systèmes optiques ; son rôle est fondamental dans l’étude de l’optique.

C’est un globe de 12 mm environ de rayon, limité par la sclérotique, membrane d’épaisseur voisine de 2 mm, dont la partie antérieure ou cornée est transparente et plus bombée (8 mm de rayon). Bien que ce ne soit pas rigoureux, nous admettrons que le diamètre commun à la cornée et au globe est un axe de révolution pour l’œil et que les différents organes constitutifs sont centrés sur cet axe.

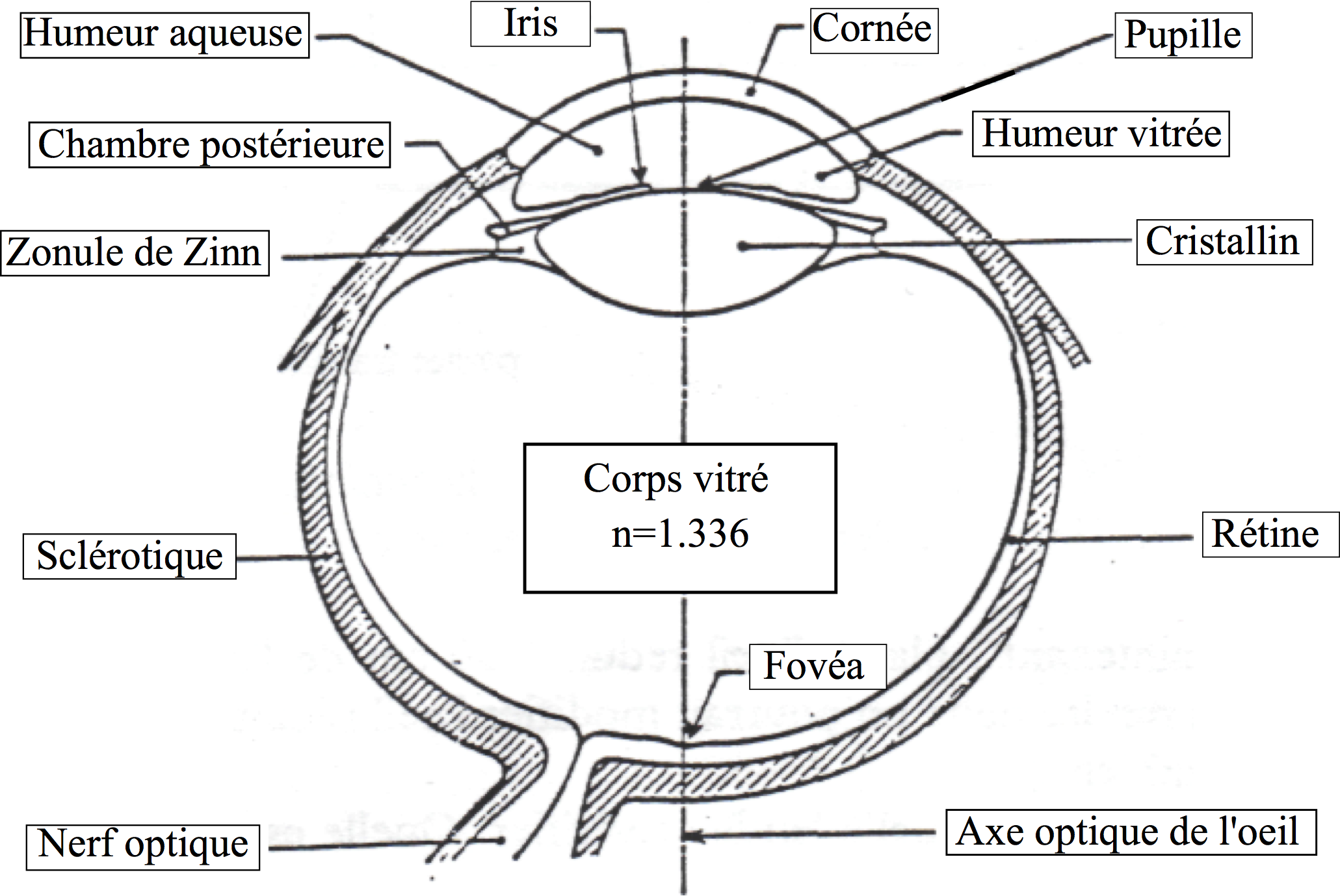
La cavité est séparée en deux compartiments par le cristallin et par une membrane ou zonule de Zinn qui s’insère sur les muscles ciliaires et sur le pourtour du cristallin.

La chambre antérieure a 4 mm d’épaisseur ; elle est remplie par l’humeur aqueuse, liquide transparent d’indice 1,336. La chambre arrière, profonde de 16 mm, contient l’humeur vitrée, masse gélatineuse d’indice 1,337.

Le cristallin est une sorte de lentille, non homogène, épaisse de 4 mm environ, formée de couches superposées capables de glisser les unes sur les autres ; son indice croît de 1,36 sur les bords à 1,42 sur l’axe ; les rayons de courbure sont respectivement de 10 mm pour la face antérieure et de 6 mm seulement pour la face postérieure ; son diamètre, enfin, est voisin de 10 mm.

En avant du cristallin est présent un diaphragme coloré, l’iris, dont l’ouverture ou pupille a un diamètre variable de 2 à 8 mm. Le fond de l’œil est tapissé par la rétine, écran sur lequel se forme l’image. Elle est l’épanouissement du nerf optique, dont les filaments aboutissent à deux sortes de cellules, de formes différentes, les cônes (diamètre 4 $\mu \mathrm{m}$) et les bâtonnets, la sensibilité des cônes étant la plus élevée en vision diurne.

La répartition des cellules n’est pas régulière : une légère dépression, la fovea centralis, de 0,3 mm de diamètre, ne comprend que des cônes et se place au centre de la tache jaune (diamètre 2 mm), elle-même riche en cônes. En fait, la sensibilité de la rétine pour la vision diurne est limitée à cette tache de surface très réduite, légèrement écartée de l’axe de l’œil.

L’axe visuel ou axe optique joint la fovea au centre optique de l’œil et fait un angle de $5^{\circ}$ environ avec l’axe géométrique.

Travail préliminaire

A l’aide de la méthode d’autocollimation, attribuer rapidement une focale à chaque lentille à disposition (si cela est possible !).
$\spadesuit$ Les noter sur votre compte-rendu.

Simulation de l’œil par un modèle très simplifié que l’on appellera l'"œil réduit"

Un œil normal (ou emmétrope) peut voir nettement des objets situés entre l’infini (punctum remotum : PR), sans accommoder, et une distance minimale de vision distincte (le punctum proximum : PP) en accommodant à fond.

Cette distance varie avec l’âge : elle est de l’ordre de 15 cm à 20 ans et s’allonge en vieillissant (cf presbytie).

On peut modéliser un "œil réduit" en réalisant un ensemble composé d’un diaphragme, d’une lentille de $+3.3\,\delta$ ($f'=30\,\mathrm{cm}$) et d’un écran.

A préparer

$\spadesuit$ Réaliser un schéma optique représentant cet œil réduit : quelle distance doit-on laisser entre la lentille et l’écran, sachant que l’œil voit net les objets situés à l’infini, sans accommoder ?
Représenter les rayons qui illustrent cette situation.

Manipulations

Réalisation de l’"œil réduit" :
Réaliser l’œil réduit sur le petit banc d’optique (sans le diaphragme), puis placer cet œil devant la fenêtre de la salle de thermodynamique (là où il y a le point d'eau) pour "regarder" le paysage avec cet "œil réduit" : ajuster la distance lentille-écran pour obtenir une image nette (d’un arbre par exemple).
$\spadesuit$ Noter cette distance pour pouvoir la réutiliser.
$\spadesuit$ Comment est l’image ?
$\spadesuit$ Pourquoi ne voyons-nous pas la même chose avec notre œil ?
Accommodation :
Reconstituer l’"œil réduit" (muni de son diaphragme ouvert complètement) sur le grand banc d’optique, à 50 cm de l’objet. L’image obtenue est floue :
$\spadesuit$ Quelle est la modification la plus simple du montage qui permet d’obtenir une image nette ?
$\spadesuit$ Cet ajustement se fait-il dans l’œil réel ?
$\spadesuit$ Comment cela se passe-t-il en réalité ?
$\spadesuit$ Comment pourrait-on modéliser ce qui se passe en réalité sur le banc d’optique ?
$\spadesuit$ En déduire ce qu’est l’accommodation ?
Rôle de la pupille :
La pupille sert d’abord à contrôler l’intensité lumineuse arrivant sur la rétine pour ne pas qu’elle soit endommagée, mais elle a aussi un autre rôle. Dans cette manipulation la distance lentille-écran n’est plus respectée.
Placer l’ensemble diaphragme-lentille à 50 cm de l’objet éclairé, l’écran à 80 cm de la lentille. Ouvrir grand le diaphragme.
$\spadesuit$ Comment est l’image ?
Fermer progressivement le diaphragme tout en observant l’écran.
$\spadesuit$ Que devient l’image ? Expliquer ces observations avec des schémas.

A préparer
Oeil myope : trop convergent. Le PP est très près de l’œil et le PR à quelques dizaines de cm seulement : les objets éloignés sont flous. On modélise l’œil myope par une lentille de $10\,\delta$ placée dans l’œil réduit, on conserve cependant la distance lentille-écran précédemment utilisée (voir la manipulation "réalisation de l’œil réduit") :
$\spadesuit$ Quel type de lentille faut-il interposer sur l’œil réduit myope pour le corriger ?
$\spadesuit$ Théoriquement, de quelle vergence doit être la lentille à interposer ?

Principe d'une lunette astronomique

Description et modélisation

Une lunette astronomique sert à observer des objets très éloignés, considérés comme à l’infini. Elle comporte un objectif convergent de distance focale de l’ordre du mètre jusqu’à 10 ou 20 m et un oculaire également convergent de distance focale de l’ordre du centimètre. Dans notre lunette simplifiée, on utilisera des lentilles dont la différence de focale est moins importante. L’"œil réduit" utilisé est celui présenté au paragraphe précédent, sans son diaphragme. Pour le reste, on dispose de trois lentilles : $2\,\delta$, $6.7\, \delta $ et $10\,\delta$.

A préparer
En plus des informations déjà données, on sait que, pour cette lunette uniquement, la lentille qui permet de simuler l’objet à l’infini a une focale environ trois fois plus petite que celle qui joue le rôle de l’objectif.
$\spadesuit$ Attribuer son rôle à chaque lentille.

On appellera :
$L$ : la lentille permettant de simuler l’objet à l’infini ;
$L_1$: l’objectif de la lunette ;
$L_2$ : l’oculaire de la lunette ;
$L'$ : la lentille de l’œil réduit.

Simulation d’une lunette afocale

Une lunette afocale donne d’un objet à l’infini une image à l’infini.

$\spadesuit$ Comment sont situés $F'_1$ et $F_2$ ?

Manipulations

Objet à l’infini :
Ajuster la position de la première lentille pour simuler l’objet à l’infini.
Réalisation de la lunette et visualisation de l’image : ajuster les positions de $L_1$, $L_2$ et $L'$ pour avoir à la fois une image nette sur l’écran de l’œil réduit et une lunette afocale (attention à l'alignement vertical des vos différents éléments optiques).

L'image sur l'écran de l"œil réduit peut ne pas être tout à fait nette: le réglage le plus crucial est celui de la lentille qui simule l'objet à l'infini, commencez donc par corriger cette position. Ensuite, vu que les lentilles sont de gros diamètres, les conditions de Gauss sont peu respectées. On peut alors interposer un diaphragme juste après la lentille qui simule l'objet à l'infini puis le fermer jusqu'à obtenir une image nette et assez lumineuse.

$\spadesuit$ Montrer sur un schéma les distances du montage (entre l’objet et la première lentille, entre les lentilles et entre la dernière lentille et l’écran).
Image intermédiaire :
Interposer le petit carré transparent quadrillé sur le trajet de la lumière entre $L_1$ et $L_2$, le déplacer sur le banc entre $L_1$ et $L_2$ jusqu’à ce que son image se forme sur l’écran de l’œil réduit (en même temps que celle de l’objet à l’infini).
$\spadesuit$ Où se trouve alors ce carré ? Justifier.
Regarder attentivement le transparent pour voir si une image (intermédiaire, dans quel sens ?) ne s’y forme pas.
$\spadesuit$ Noter les observations et expliquer.

Grossissement d’une lunette afocale

Sur le montage complet de la lunette, mesurer (sur l’écran de l’œil réduit) la hauteur de l’image $\overline{A'B'}$ de l’objet à l’infini $\overline{AB}$.
$\spadesuit$ Noter la mesure de $\overline{A'B'}$.
$\spadesuit$ Faire un schéma montrant l’oculaire de la lunette et l’œil réduit, tracer sur celui-ci les rayons parallèles qui sortent de la lunette et qui pénètrent dans l’œil pour former l’image $\overline{A'B'}$.
$\spadesuit$ Relier $\theta'$, angle sous lequel est vue cette image, à $f'$ focale de l’œil réduit, et $\overline{A'B'}$.
Enlever $L_1$ et $L_2$ : mesurer la hauteur de l’image $\overline{A'_0B'_0}$, formée sur l’écran de l’œil réduit sans lunette, mais avec l’objet à l’infini (rapprocher l’œil).
$\spadesuit$ Noter la mesure de $\overline{A'_0B'_0}$.
$\spadesuit$ Faire un schéma montrant la lentille permettant de simuler l’objet à l’infini et l’"œil réduit", tracer sur celui-ci les rayons parallèles qui sortent de l’objet et qui pénètrent dans l’œil pour former l’image $\overline{A'_0B'_0}$.
$\spadesuit$ Relier $\theta$, angle sous lequel est vu l’objet à f’ focale de l’"œil réduit", et $\overline{A'_0B'_0}$.
$\spadesuit$ En déduire le grossissement de la lunette $G = \theta'/\theta$ :
$\theta'$ : angle sous lequel on voit l’objet à travers la lunette.
$\theta$ : angle sous lequel on voit l’objet à l’œil nu .
Relier $G$ à $f'_1$ et $f'_2$.
$\spadesuit$ Écrire la relation en l’expliquant à l’aide d’un schéma ; calculer $G$ avec ces focales. Comparer avec le résultat pratique.

Ce grossissement est qualifié d’intrinsèque : il ne dépend pas de l’observateur. Dans les instruments réels, il varie de quelques dizaines pour les petites lunettes jusqu’à plus de 3000 pour les meilleures.

Cercle oculaire de la lunette

Le cercle oculaire est l’image de l’objectif par l’oculaire.

A préparer
$\spadesuit$ A bonne échelle, faire un schéma précis montrant la construction du cercle oculaire de cette lunette.

Enlever l’"œil réduit". Glisser, collé à l’objectif, la pointe d’un stylo dans le faisceau lumineux. Déplacer l’écran jusqu’à observer l’image nette de cette pointe. Dans cette configuration, la position de l’écran correspond à la position du cercle oculaire.
$\spadesuit$ Noter cette position.
$\spadesuit$ Mesurer le diamètre du cercle oculaire.
$\spadesuit$ Calculer la position de ce cercle (par rapport à $O_2$, centre de la lentille $L_2$) : vérifier expérimentalement cette valeur.
$\spadesuit$ Calculer son diamètre. Comparer la valeur du calcul avec la valeur mesurée. Commenter l’écart obtenu et conclure en observant attentivement le trajet de la lumière sur ce montage.

C’est évidemment au cercle oculaire qu’il faut placer l’œil. Pour une bonne lunette, le cercle oculaire est plus petit que la pupille, ainsi l’œil reçoit toute la lumière sortant de l’instrument.

Que mettre dans le fichier de résultats à poster ?

Pour rappel, vous devez déposer votre fichier ici à l'issue du TP

On commentera et discutera tous les résultats/courbes de cette feuille de résultats

On consignera les résultats suivants :
- Pour ce TP vous pouvez faire des photos d'un de vos cahiers puis en faire un document pdf.
- Les deux schémas qui expliquent comment la pupille permet d'améliorer la netteté d'une image qui serait floue.
- Un schéma montrant la succession de lentilles (de gauche à droite) que vous avez utilisées pour modéliser la lunette astronomique, avec les distances entre elles (pas besoin de rayons lumineux) ;
- Le schéma qui relie $f'$, $\theta$ et $\overline{A'B'}$, et celui qui relie $f'$, $\theta'$ et $\overline{A_0B_0}$. La mesure de $\overline{A'B'}$, la mesure de $\overline{A_0B_0}$, ainsi que la valeur du grossissement obtenu ;
- Les mesures et calculs obtenus pour le cercle oculaire : position et taille expérimentales, position et taille théoriques.

Annexe : liste de matériel

Une lampe quartz-iode ;
Une alimentation alternative 12V ;
Un banc optique d'une longueur de deux mètres plus un ensemble de pieds adaptés (5 au moins) ;
Un petit banc d'optique de 50cm de long muni de deux supports pour lentille/écran ;
Un ensemble de lentilles convergentes de différentes focales identifiées avec des lettres sur supports adaptés au banc optique ;
Un écran blanc pouvant se positionner sur un pied du banc optique ;
Un support de diapositive pouvant se positionner sur un pied du banc optique ;
Une diapositive objet transparente mais dépolie ;
une diapositive quadrillage en papier transparent ;
Un diaphragme
Un miroir