TP-cours : circuit RLC en régime libre - CORRECTION
Vidéo
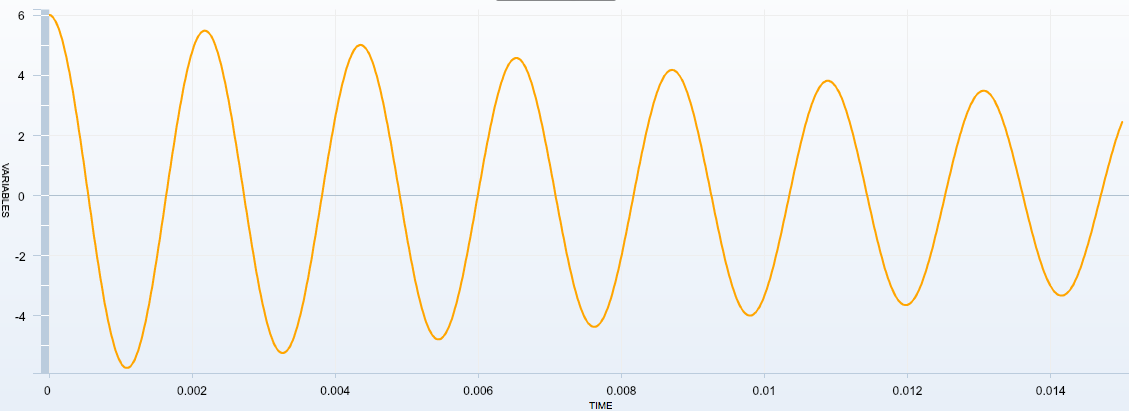
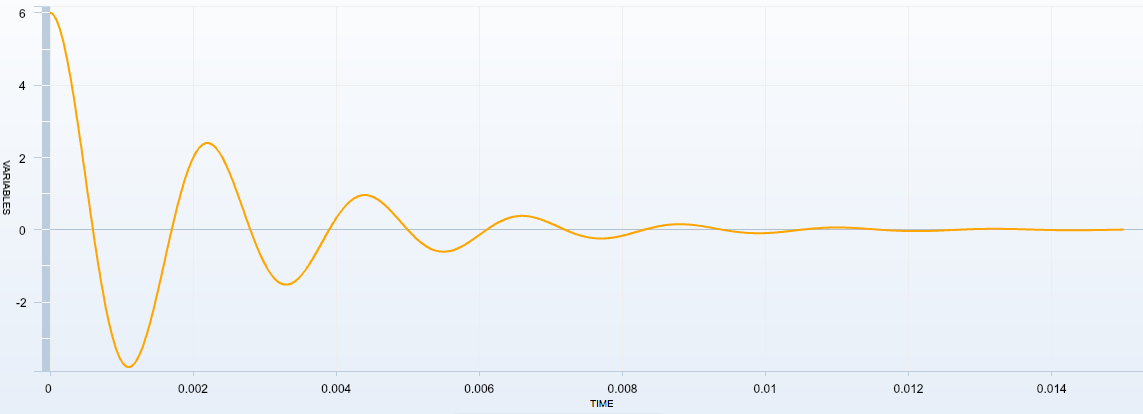
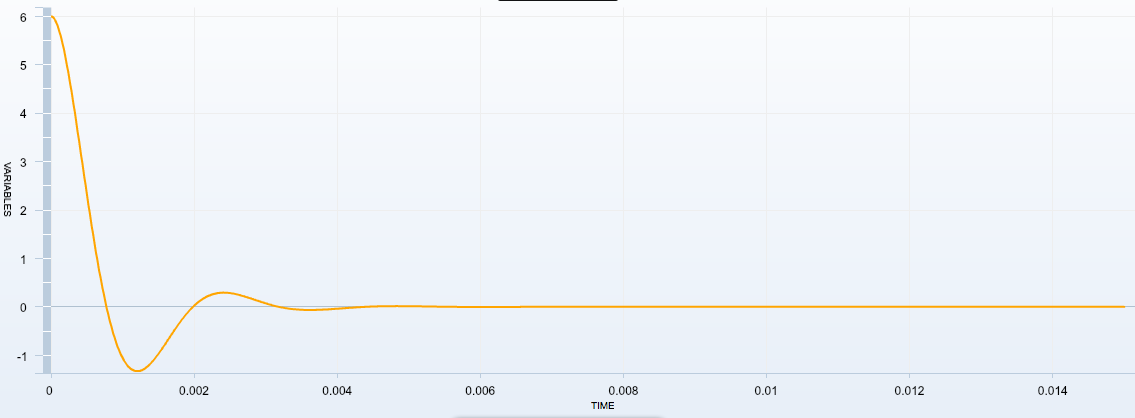
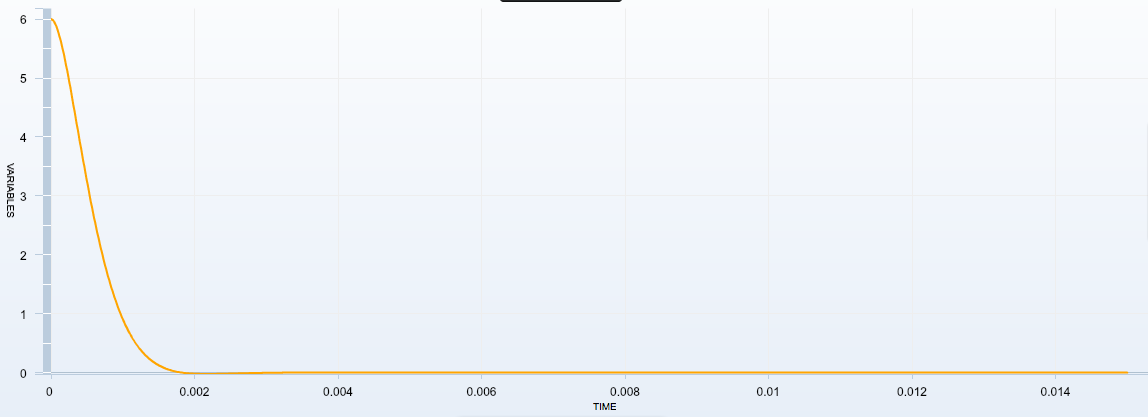
Existence de différents régimes : influence de la résistance du conducteur ohmique
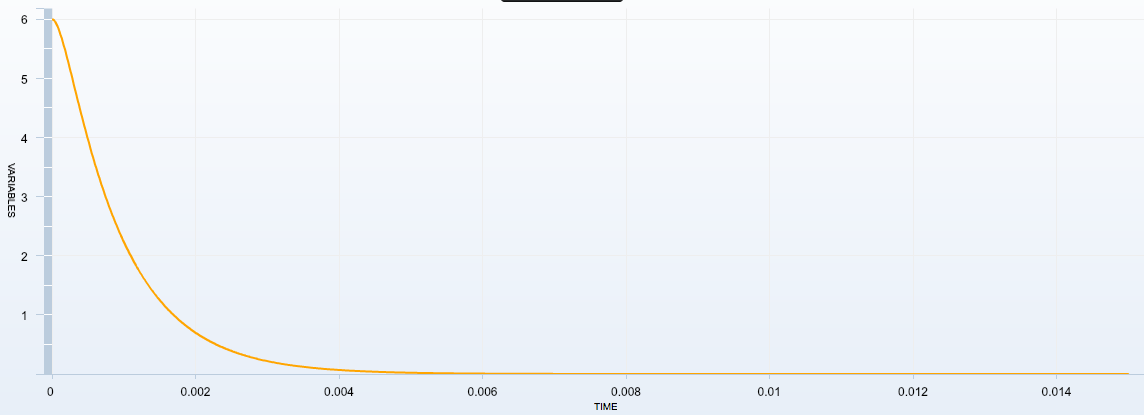
Questions
| $R\,$($\Omega$) | 100 | 1000 | 3000 | 6000 | 10000 |
| $Q$(s) | 31,6 | 3,16 | 1,05 | 0,53 | 0,32 |
| Régime | Pseudo-périodique | Pseudo-périodique | Pseudo-périodique | Pseudo-périodique proche du critique | Apériodique |
Etude du régime pseudo-périodique
Pseudo-période et période propre, différences
- On parle de pseudo-période car le signal est périodique mais les amplitudes des oscillations diminuent au cours du temps.
- 7 périodes pour un temps de $1,392 \times 10^{-2}\,\mathrm{s}$, donc une période de $1,989 \times 10^{-3}\,\mathrm{s}$.
Or la période propre vaut $2\pi\sqrt{LC} = 1,987\,\mathrm{s}$.
Ces périodes sont pratiquement égales.
Voici l'acquisition des oscillations qui se produiraient s'il n'y avait pas de résistance :
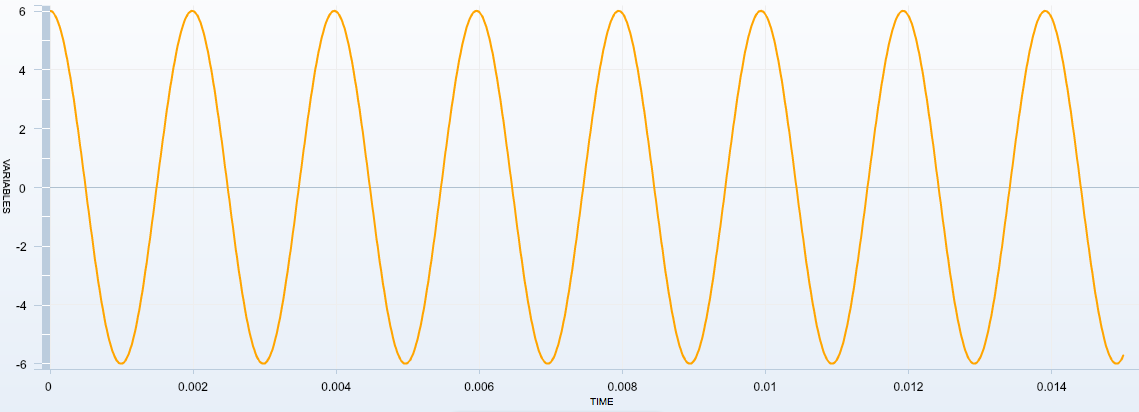
Cette courbe permet de "mesurer" la période propre du circuit.
Influence de $R$
Oui, la valeur de la résistance du conducteur ohmique influe sur la pseudo-période des oscillations, mais cette influence est plutôt faible.
En effet, la théorie indique que la pseudo-période des oscillations est donnée par $T = \frac{2\pi}{\sqrt{\omega_0^2-\lambda^2}}$ où $\lambda = \dfrac{R}{2L}$. La résistance intervient bien.
Influence de $L$
- Mesures
| $L$ (H) | 1,2 | 1,0 | 0,8 | 0,6 | 0,4 |
| $T$ (s) | $2,18 \times 10^{-3}$ | $1,99 \times 10^{-3}$ | $1,78 \times 10^{-3}$ | $1,54 \times 10^{-3}$ | $1,26 \times 10^{-3}$ |
- Plus l'inductance de la bobine diminue, plus la pseudo-période des oscillations diminue, cela est conforme à la formule donnant la pseudo-période des oscillations : $T = \frac{2\pi}{\sqrt{\dfrac{1}{LC}-\lambda^2}}$
Si $L$ diminue, $\dfrac{1}{LC}$ augmente donc $T$ diminue.
Influence de $C$
-
Mesures
| $C\,$($\mathrm{\mu\,F}$) | 0,1 | 0,5 | 1,0 | 1,5 | 2,0 |
| $T$ (s) | $2,18 \times 10^{-3}$ | $4,43 \times 10^{-3}$ | $6,28 \times 10^{-3}$ | $7,7 \times 10^{-3}$ | $8,9 \times 10^{-3}$ |
- Plus la capacité du condensateur augmente, plus la pseudo-période des oscillations augmente, ce qui est en accord avec la théorie puisque $T = \frac{2\pi}{\sqrt{\dfrac{1}{LC}-\lambda^2}}$
Si $C$ augmente, $\dfrac{1}{LC}$ diminue donc $T$ augmente.
Etude du régime critique
- D'après nos premières simulations, on sait que le régime critique est obtenu pour une résistance proche de $6000\,\Omega$
- Ceci nous donne un facteur de qualité de 0,53 proche des 0,5 attendu
- On trouve pour $u_C = 2\,E\,e^{-1}$, $t = 3,133 \times 10^{-4} = \dfrac{1}{\lambda}$ d'où $\lambda = 3192$. Or $Q = \dfrac{\omega_0}{2\,\lambda} = \dfrac{1}{\sqrt{LC}2\,\lambda} = 0.495$.
CQFD aux arrondis près.
Exercice : circuit LC série réel
- On applique la loi des nœuds à l'endroit de la dérivation :
\begin{equation}
i(t) = C\dfrac{du}{dt} + \dfrac{u}{R}
\end{equation}
Puis la loi des mailles dans la branche principale :
\begin{align} L\dfrac{di}{dt} + R\,i + u = E\\ \Longleftrightarrow LC\dfrac{d^2u}{dt^2} + \dfrac{L}{R} \dfrac{du}{dt} + RC \dfrac{du}{dt} + u + u = E\\ \Longleftrightarrow \tau^2 \dfrac{d^2u}{dt^2} + 2\tau \dfrac{du}{dt} + 2u = E\\ \Longleftrightarrow \boxed{\dfrac{d^2u}{dt^2} + \dfrac{2}{\tau}\dfrac{du}{dt} + \dfrac{2}{\tau^2}u = \dfrac{E}{\tau^2}} \end{align}
La solution de cette équation est la somme de la solution de l'équation sans second membre et de la solution particulière.
Solution particulière
Cette dernière est constante et s'écrit $u_P = \dfrac{E}{2}$.
Solution homogène
Pour trouver la solution de l'équation homogène, on cherche les racines du polynôme caractéristique $r^2 + \dfrac{2}{\tau}r + \dfrac{2}{\tau^2} = 0$.
Le discriminant réduit est $\Delta' = b'^2 - ac = \dfrac{1}{\tau^2} - 1\times \dfrac{2}{\tau^2} = -\dfrac{1}{\tau^2} < 0$ donc les racines de ce polynôme sont
\begin{equation} r_1 = -\dfrac{1}{\tau}+j\dfrac{1}{\tau} \hspace{2cm} r_2 = -\dfrac{1}{\tau}-j\dfrac{1}{\tau} \end{equation}
Pour se ramener à ce qui a été vu dans le cours, si on pose $\lambda = -\dfrac{1}{\tau}$ et $\omega = \dfrac{1}{\tau}$, la solution s'écrit :
\begin{equation} u_H(t) = (A_1 \cos(\omega t) + A_2 \sin(\omega t))e^{-\lambda t} \end{equation} Donc ici :
\begin{equation} u_H(t) = \left(A_1 \cos\left(\dfrac{t}{\tau}\right) + A_2 \sin\left(\dfrac{t}{\tau}\right)\right)e^{-\dfrac{t}{\tau}} \end{equation}
Solution globale
Finalement, la solution s'écrit :
\begin{align} \boxed{u(t) = \dfrac{E}{2} + \left(A_1 \cos\left(\dfrac{t}{\tau}\right) + A_2 \sin\left(\dfrac{t}{\tau}\right)\right)e^{-\dfrac{t}{\tau}}} \end{align}
Détermination des constantes
Les conditions initiales sont $u(t=0)=0$ et $i(t=0)=0$, ainsi :
- La première condition donne :
\begin{equation}
A_1 = -\dfrac{E}{2}
\end{equation}
- Pour utiliser la deuxième condition, on doit dériver u(t) :
\begin{align}
i(t) = C\dfrac{du}{dt} &= C\left(-\dfrac{A_1}{\tau}\sin\left(\dfrac{t}{\tau}\right)+\dfrac{A_2}{\tau}\cos\left(\dfrac{t}{\tau}\right)\right)e^{-\dfrac{t}{\tau}}\\
& + C\left(A_1 \cos\left(\dfrac{t}{\tau}\right) + A_2 \sin\left(\dfrac{t}{\tau}\right)\right) \left(-\dfrac{1}{\tau}\right)e^{-\dfrac{t}{\tau}}
\end{align}
Donc :
\begin{equation} i(t=0) = \dfrac{A_2}{\tau}-\dfrac{A_1}{\tau} = 0 \Longleftrightarrow A_2=-\dfrac{E}{2} \end{equation}
La tension aux bornes du condensateur s'écrit :
\begin{equation} u(t) = \dfrac{E}{2} \left(1-e^{-\dfrac{t}{\tau}}\left(\cos\left(\dfrac{t}{\tau}\right) + \sin\left(\dfrac{t}{\tau}\right)\right)\right) \end{equation}
- La première condition donne :
\begin{equation}
A_1 = -\dfrac{E}{2}
\end{equation}
- En régime permanent, la bobine se comporte comme un interrupteur fermé, le condensateur comme un interrupteur ouvert. Donc le circuit étudié devient celui de la figure ci-contre.
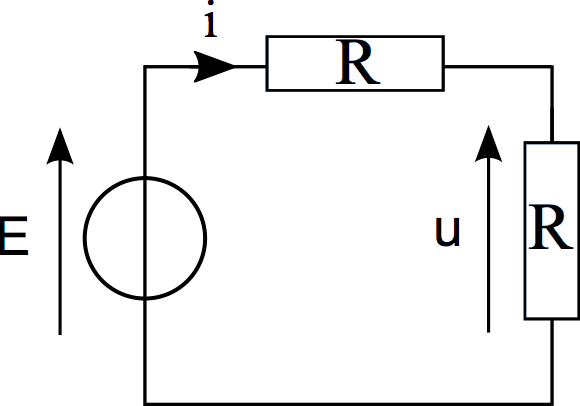
Ainsi on a :
\begin{equation} u = \dfrac{R}{2R}E = \dfrac{E}{2} \hspace{0.5cm} \text{(diviseur de tension)} \end{equation} et :
\begin{equation} i= \dfrac{E}{2R} \qquad \text{(loi d'Ohm)} \end{equation}


