TP focométrie
Objectifs : déterminer la distance focale de divers lentilles minces par plusieurs méthodes.
Rappels
Lentilles ...
- Une lentille est un milieu transparent limité par deux dioptres, les deux peuvent être sphériques ou l’un est sphérique et l’autre est plan. Dans ce TP, nous étudierons des lentilles minces : une lentille est mince si son diamètre est très grand devant son épaisseur.
- Le centre de la lentille est noté O et est appelé centre optique et il est considéré comme ponctuel. Tout rayon passant par O n’est pas dévié par la lentille.
- L’axe optique de la lentille est l’axe qui passe par le centre optique O et qui est perpendiculaire à la lentille.
- On distingue deux sortes de lentille :
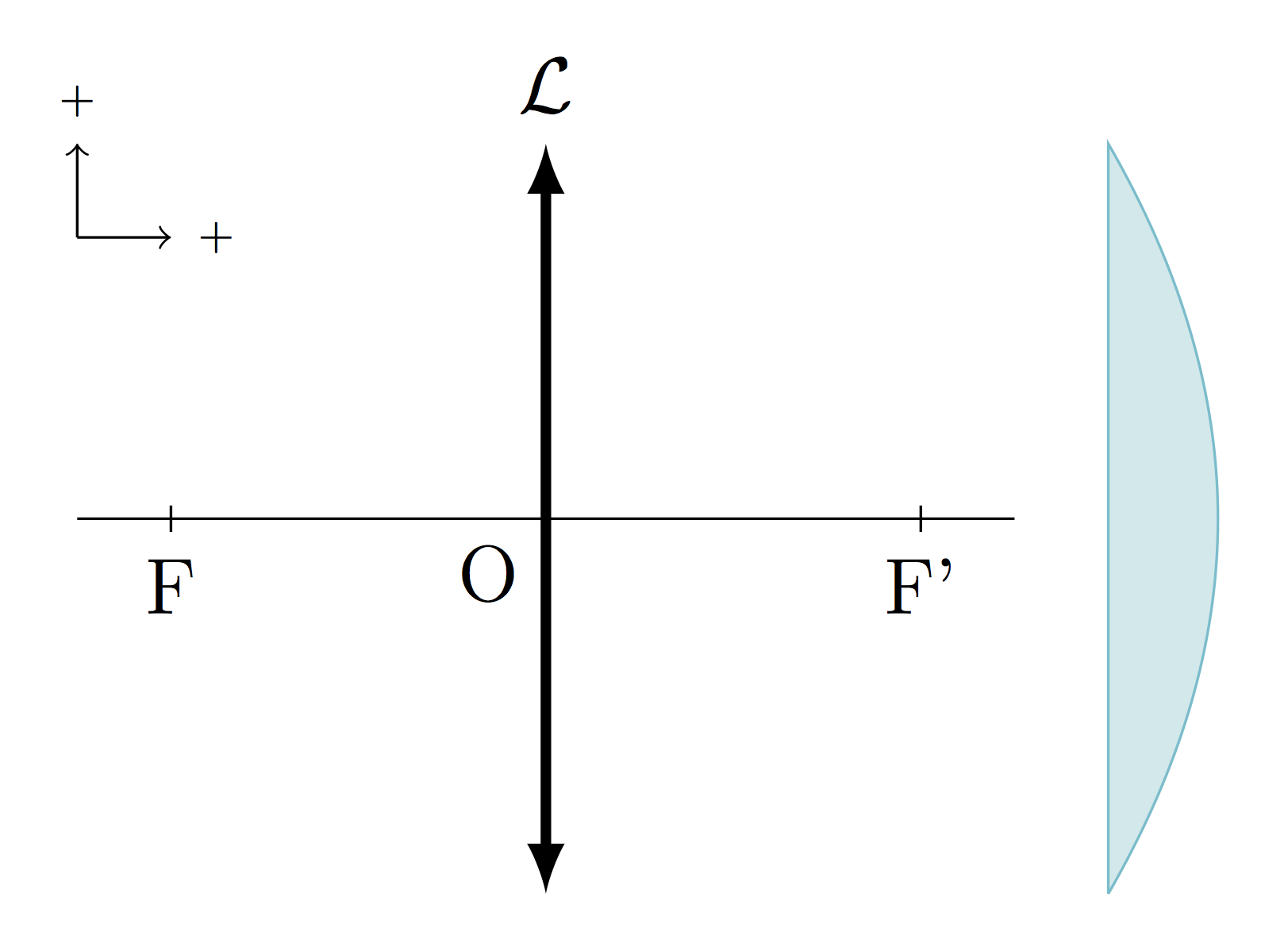
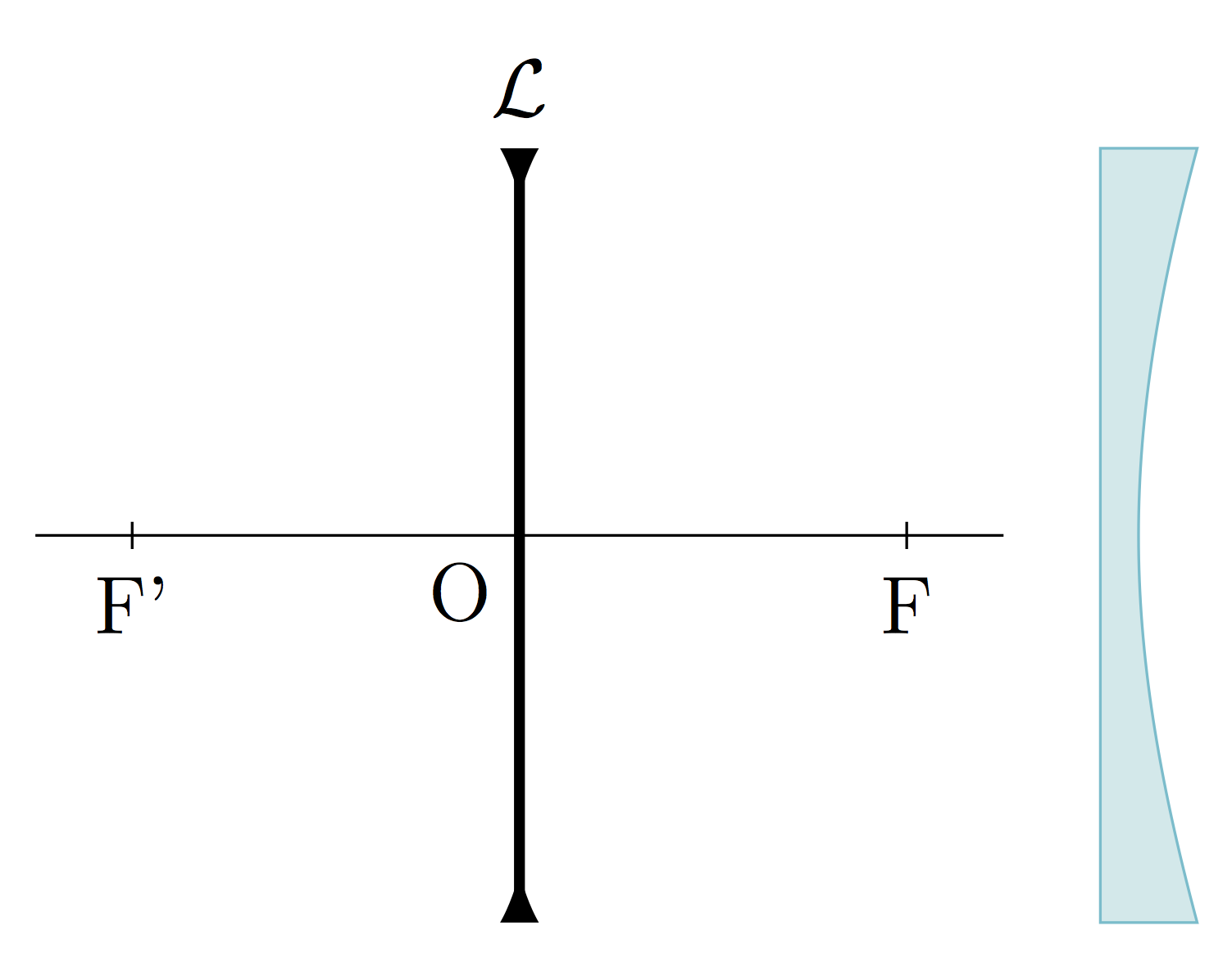
Foyers
Foyer principal objet
Ce foyer noté F est le point dont l’image est situé à l’infini sur l’axe optique. Tout rayon incident passant par F émerge parallèle à l’axe optique. Ainsi, on obtient les deux constructions suivantes pour les lentilles convergente et divergente :
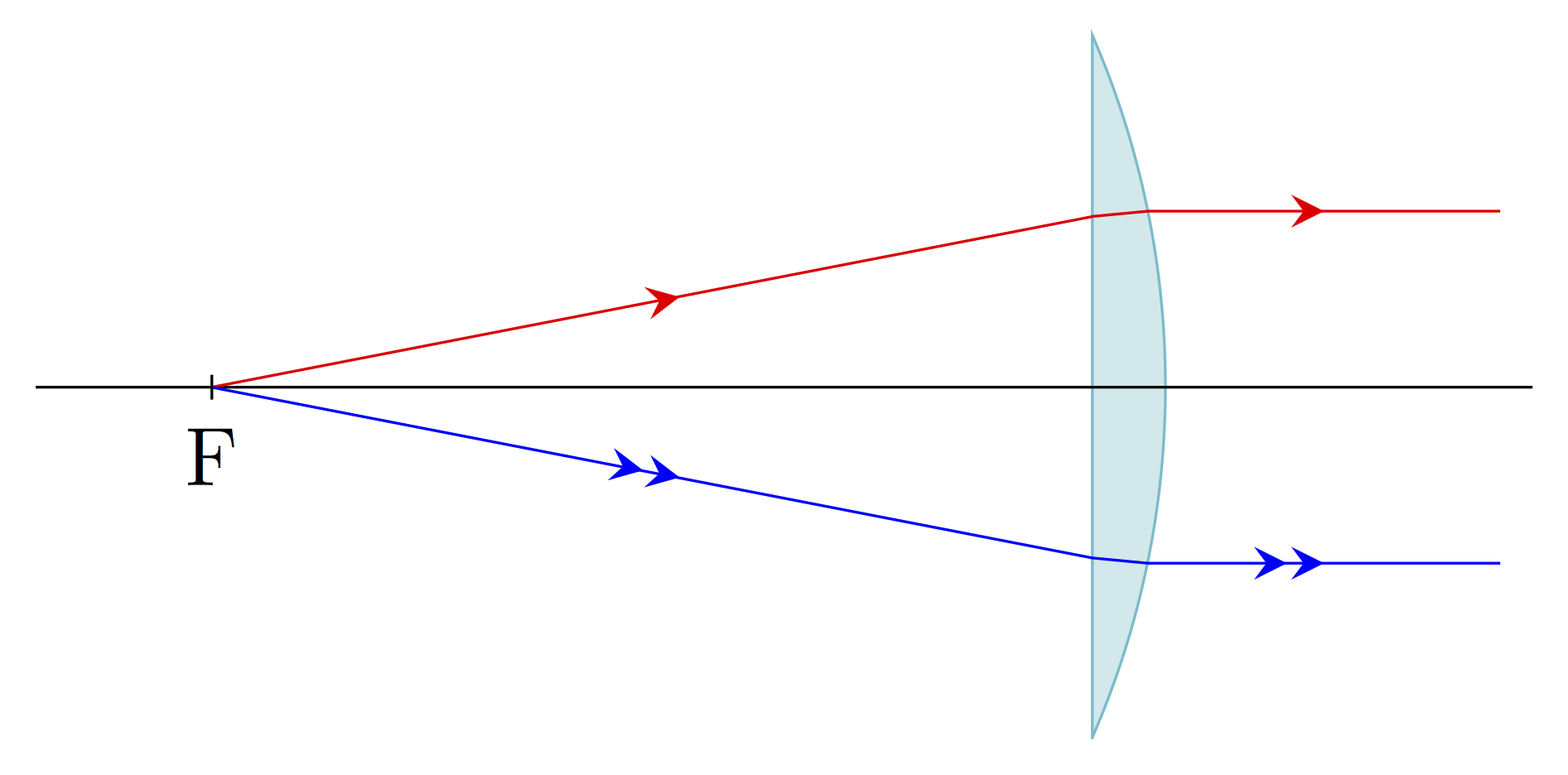
La distance \(f = \overline{OF}\) est appelée distance focale objet, c’est une grandeur algébrique. Elle est négative dans le cas d’une lentille convergente, positive dans le cas d’une lentille divergente.
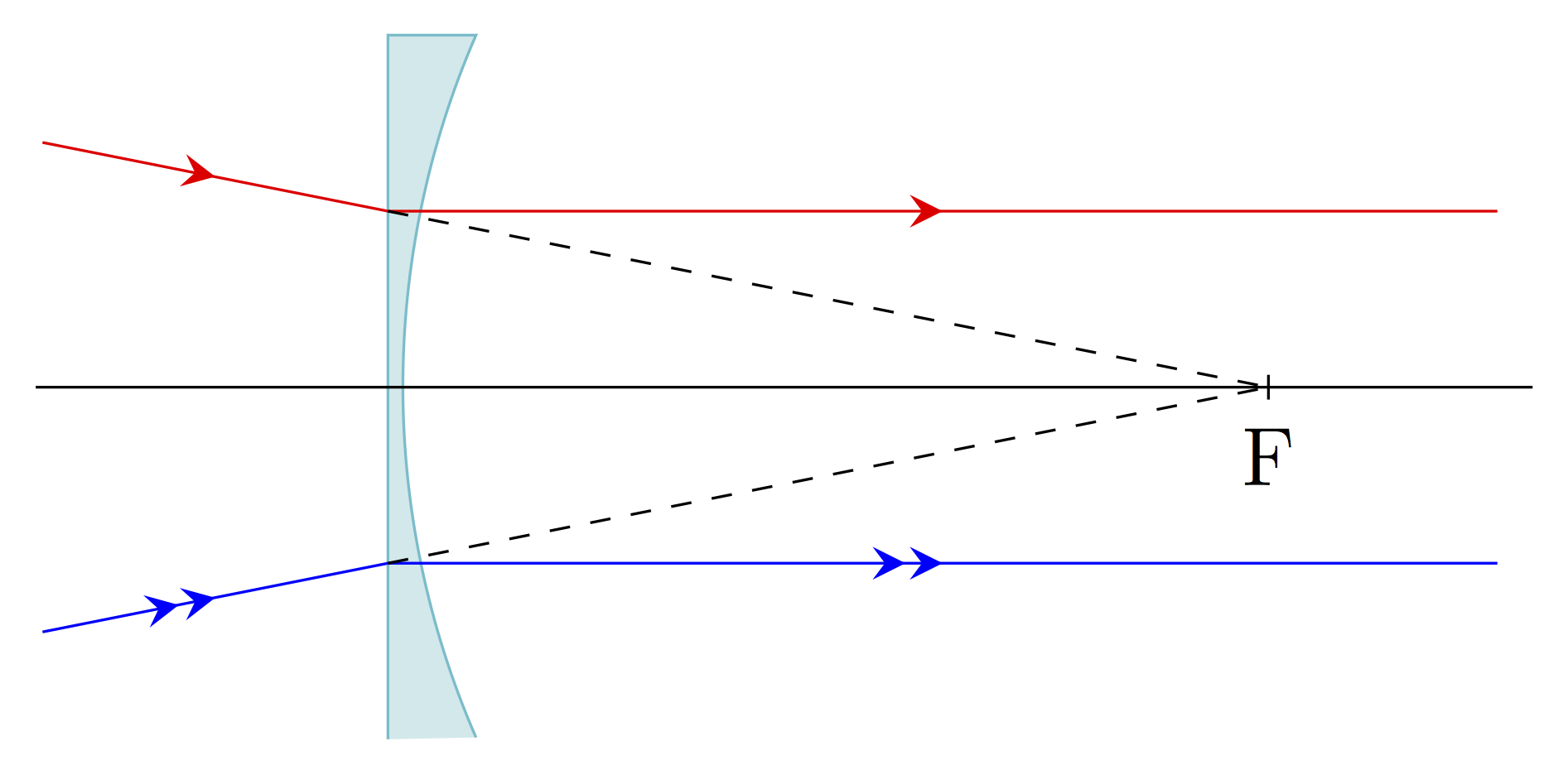
Foyer principal image
Ce foyer noté F’ est le point image d’un point objet situé à l’infini sur l’axe optique. Tout rayon incident parallèle à l’axe optique émerge en passant par F’. Ainsi, on obtient les deux constructions suivantes pour les lentilles convergente et divergente :
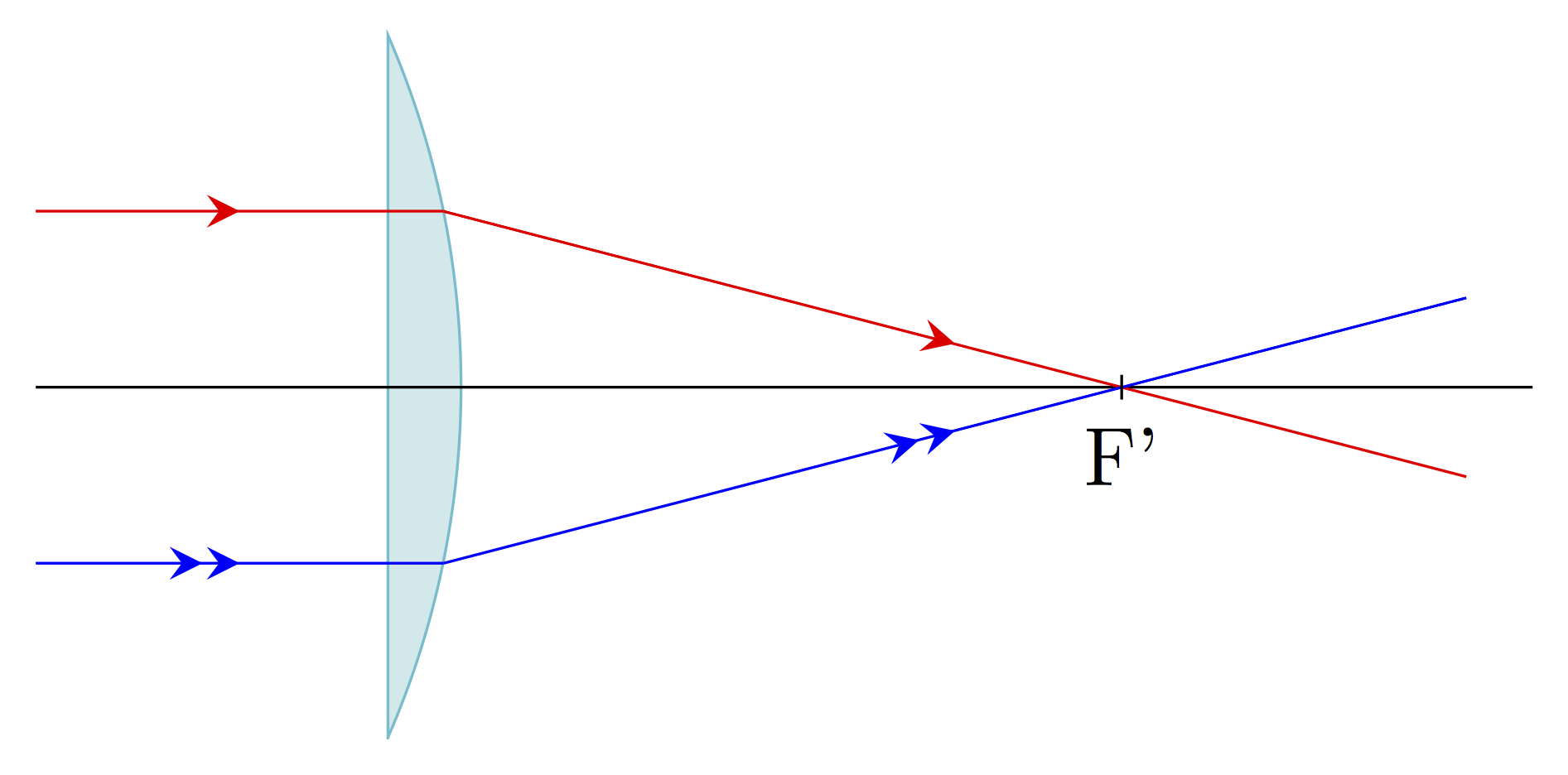
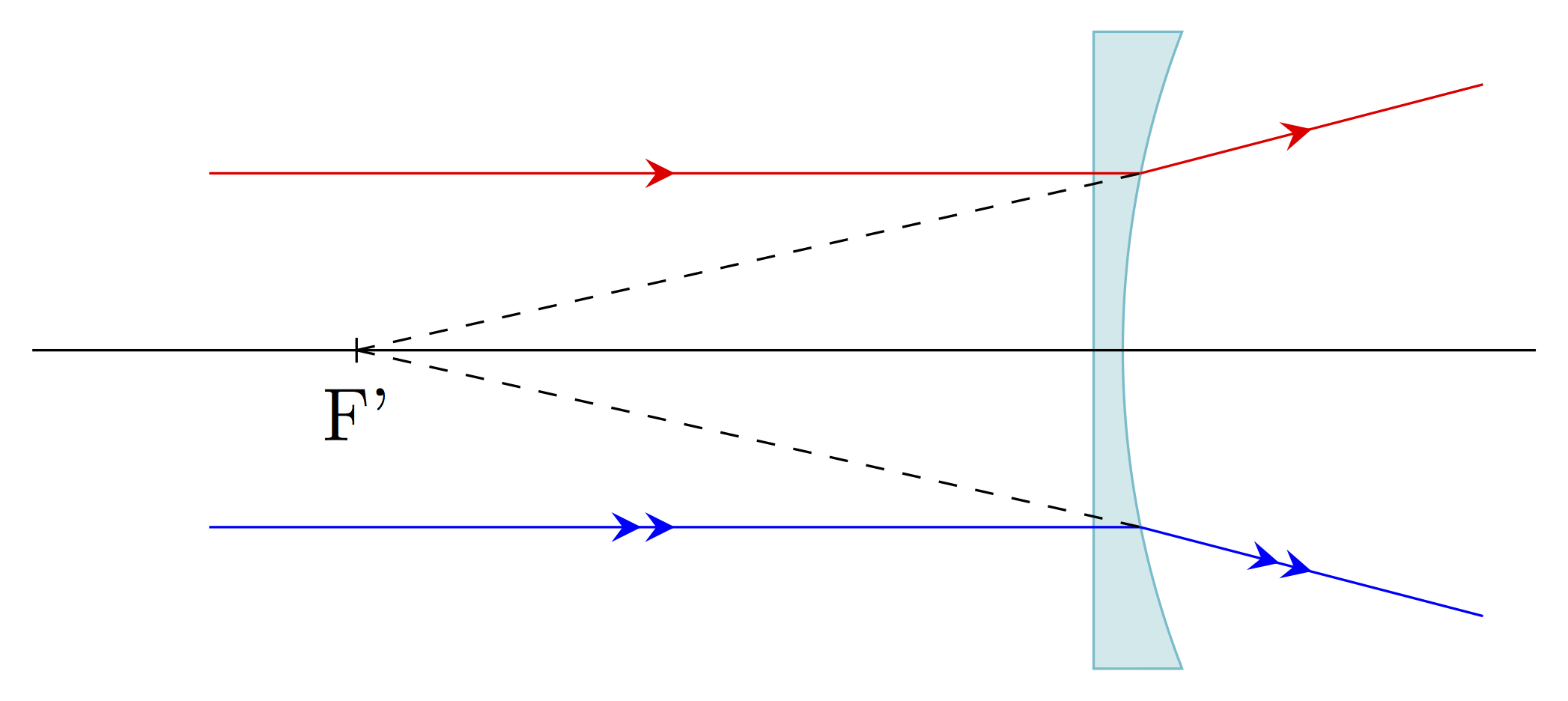
La distance \(f' = \overline{OF'}=-\overline{OF}\) est appelée distance focale image, c’est une grandeur algébrique. Elle est négative dans le cas d’une lentille divergente, positive dans le cas d’une lentille convergente.
Vergence
La vergence d’une lentille permet de caractériser sa convergence ou sa divergence. Elle est définie par :
\begin{equation*} \boxed{V = \dfrac{1}{f'}} \quad \heartsuit \end{equation*}
et s’exprime en dioptrie (symbole \(\delta\)) si \(f'\) est exprimée en mètre (\(\mathrm{m}\)).
Cette vergence est positive pour une lentille convergente et négative pour une lentille divergente. Plus la valeur de \(V\) est grande en valeur absolue, plus la lentille est convergente ou divergente selon le cas.
Objets et images
Réel ou virtuel
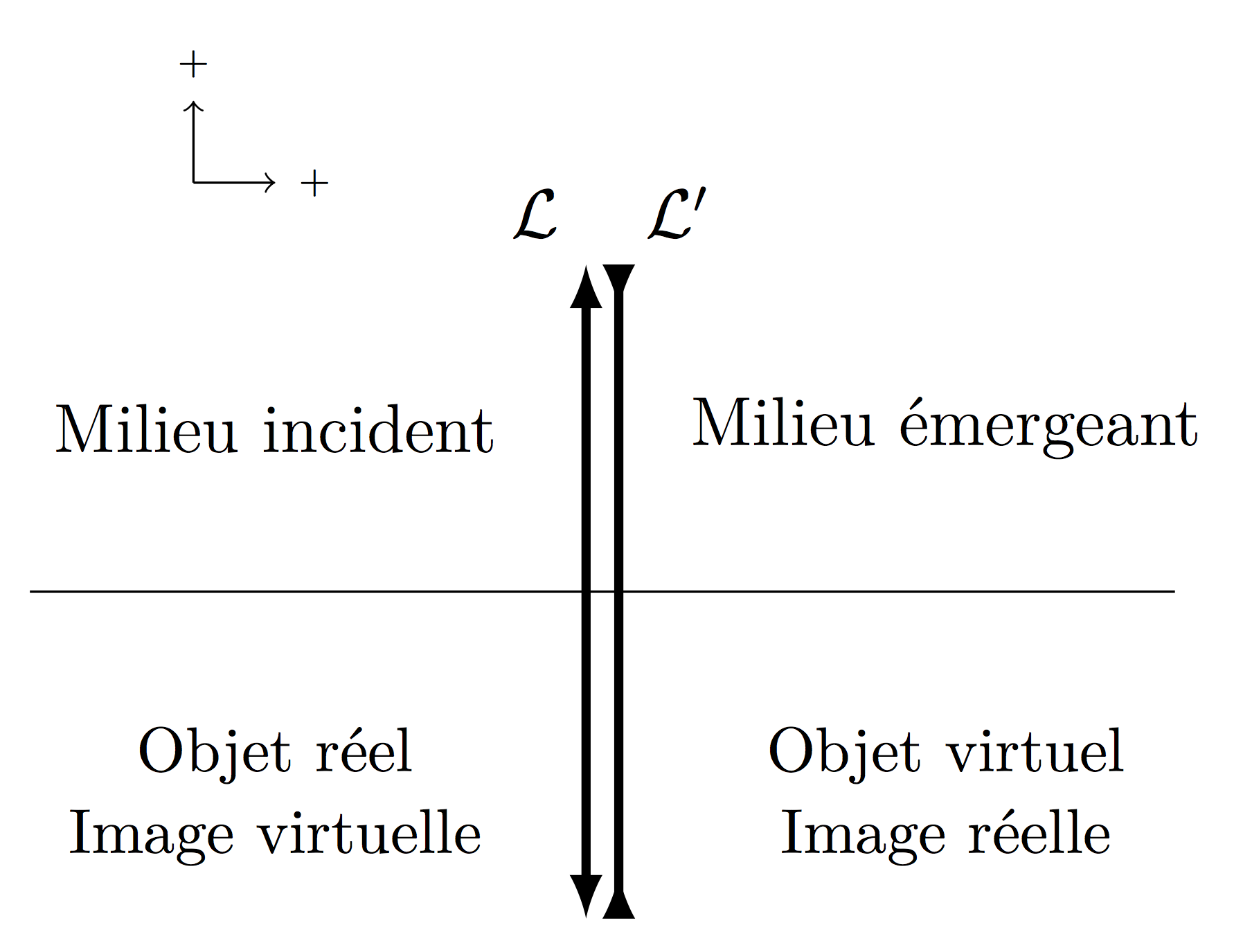
- Objet réel : source lumineuse placée avant la lentille ; les rayons incidents proviennent de cette source.
- Image réelle : point où convergent réellement tous les rayons émergents ; peut être reçue sur un écran.
- Image virtuelle : image qui ne peut pas être matérialisée sur un écran directement ; les rayons émergents ne convergent pas en ce point, seuls leurs prolongements fictifs (pointillés) y convergent.
- Objet virtuel : le prolongement des rayons incidents convergent en ce point ; les rayons incidents viendraient converger en ce point s’il n’y avait pas de lentille.
Points conjugués
A’ est l’image conjuguée de A si tous les rayons (ou leur prolongement) issus de A émergent en passant par A’.
Formule de conjugaison de Descartes
|
\begin{equation*}\boxed{\dfrac{1}{f'} = \dfrac{1}{\overline{OA'}} - \dfrac{1}{\overline{OA}}}\quad \heartsuit\end{equation*} |
Avec \(f'\), \(\overline{OA'}\) et \(\overline{OA}\) exprimées en mètre (\(\mathrm{m}\)). |
Formule de grandissement
|
\begin{equation*}\boxed{\gamma = \dfrac{\overline{OA'}}{\overline{OA}} = \dfrac{\overline{A'B'}}{\overline{AB}}}\quad \heartsuit\end{equation*} |
Avec \(\overline{AB}\) la taille de l’objet et \(\overline{A'B'}\) la taille de l’image. |
Manipulations
Généralités
Vous disposez d’un banc d’optique gradué, tous les éléments (lentilles, objet, écran ...) se montent sur des pieds munis de repères permettant la mesure sur celui-ci. Attention, ce repère ne correspond pas toujours à la position de l’élément (il faut en tenir compte).
Attention : la lampe est alimentée par une alimentation stabilisée et la tension aux bornes de la lampe ne doit pas dépasser une certaine valeur (indiquée).
Procédures
- Pour mesurer un grandissement \(\gamma\), mesurer une partie de l’objet puis l’image de cette partie et procéder au calcul.
- Identification des lentilles : pour reconnaître si une lentille est convergente ou divergente, il faut tenir la lentille à bout de bras et observer un objet éloigné à travers cette lentille : si l’image (même floue) est inversée alors vous tenez une lentille convergente ; sinon, elle est divergente. On peut également tester l’effet loupe : si la lentille joue le rôle de loupe alors elle est convergente ; et plus sa vergence est grande, plus l’effet loupe est important. Une lentille divergente ne joue pas le rôle de loupe. \(\spadesuit\) Question :
Séparer les lentilles convergentes des lentilles divergentes : indiquer les lettres des lentilles convergentes et les lettres des lentilles divergentes. - Évaluation des incertitudes : dans toutes les mesures, on estimera donc la précision avec laquelle les résultats sont obtenus. Dans ce TP, il s’agit souvent d’estimer une plage de valeurs acceptables et d’utiliser la formule adéquate pour évaluer l’incertitude-type de type B. Il ne s’agit pas seulement de remplir des tableaux : il faut aussi critiquer les résultats.
- Important si la lentille étudiée est très bombée : si on décide de ne faire qu’une seule mesure : utiliser la "règle des 3 p" : toujours mettre la face la plus plane de la lentille vers l’élément du banc d’optique le plus proche (écran, objet ou autre lentille). Pour plus de rigueur expérimentale, faire 2 mesures (important sur la lentille est très bombée) : une pour chaque face de la lentille et faire la moyenne des 2 si la cohérence des résultats est bien là.
Lentille convergente
Vous étudierez la lentille J ou W (selon la paillasse), toutes les méthodes seront testées avec cette lentille : les résultats doivent concorder !
Autocollimation
Principe
On place contre la face de sortie de la lentille un miroir plan, on déplace l’ensemble (lentille + miroir) jusqu’au moment où l’image A’B’ de AB apparaît nette, sur la diapositive objet mais avec une inversion \((\overline{A'B'}=-\overline{AB}).\) L’objet est alors au foyer objet de la lentille : \(\overline{AO}=\overline{FO}=f'\).
Explication
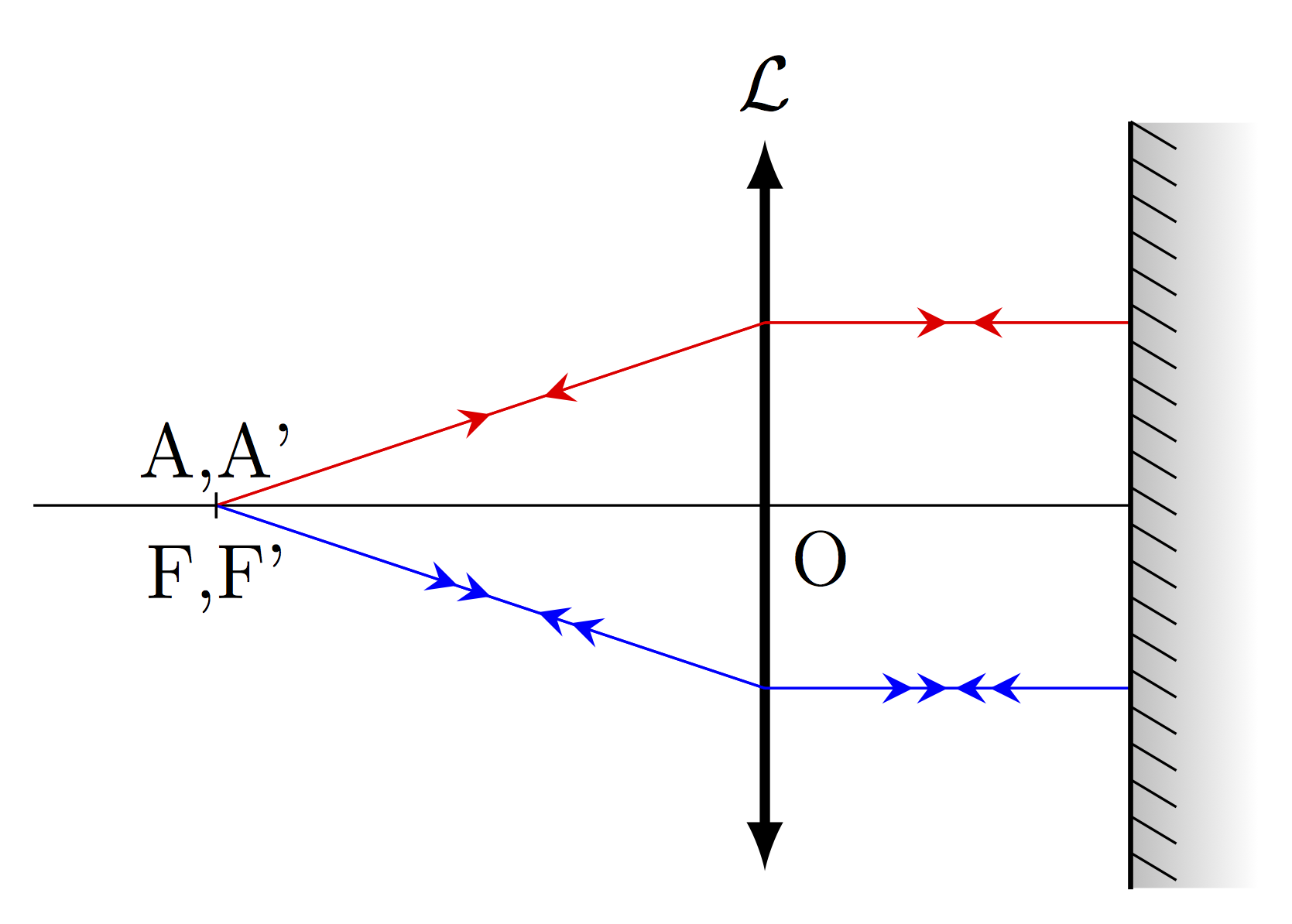
En effet, les rayons sortent de la lentille parallèlement à l’axe et arrivent donc sous incidence nulle sur le miroir. Ils sont donc réfléchis sur eux-mêmes c’est-à-dire parallèlement à l’axe. Puis, comme la lumière a changé de sens, après traversée de la lentille ils vont donc converger au foyer image.
On a ainsi réalisé un collimateur : lentille + source à son foyer objet.
Manipulation
- On utilise la diapositive objet composée de carrés/flèches noirs et blancs.
- Réaliser l’autocollimation sur la lentille étudiée.
\(\spadesuit\) La distance lentille - miroir doit-elle avoir une valeur particulière ? - \(\spadesuit\) Mesurer \(f'\) et évaluer l’incertitude \(U_f'\) (à 95%). Critiquer les résultats.
- \(\spadesuit\) Avec \(AB\) et \(A'B'\) (prendre comme objet AB une longueur caractéristique de la diapositive), mesurer \(\gamma\). Conclure.
Attention aux différents reflets : l’image cherchée est la plus lumineuse de toutes et elle doit bouger si on bouge un peu le miroir latéralement.
Méthode de l’objet à l’infini
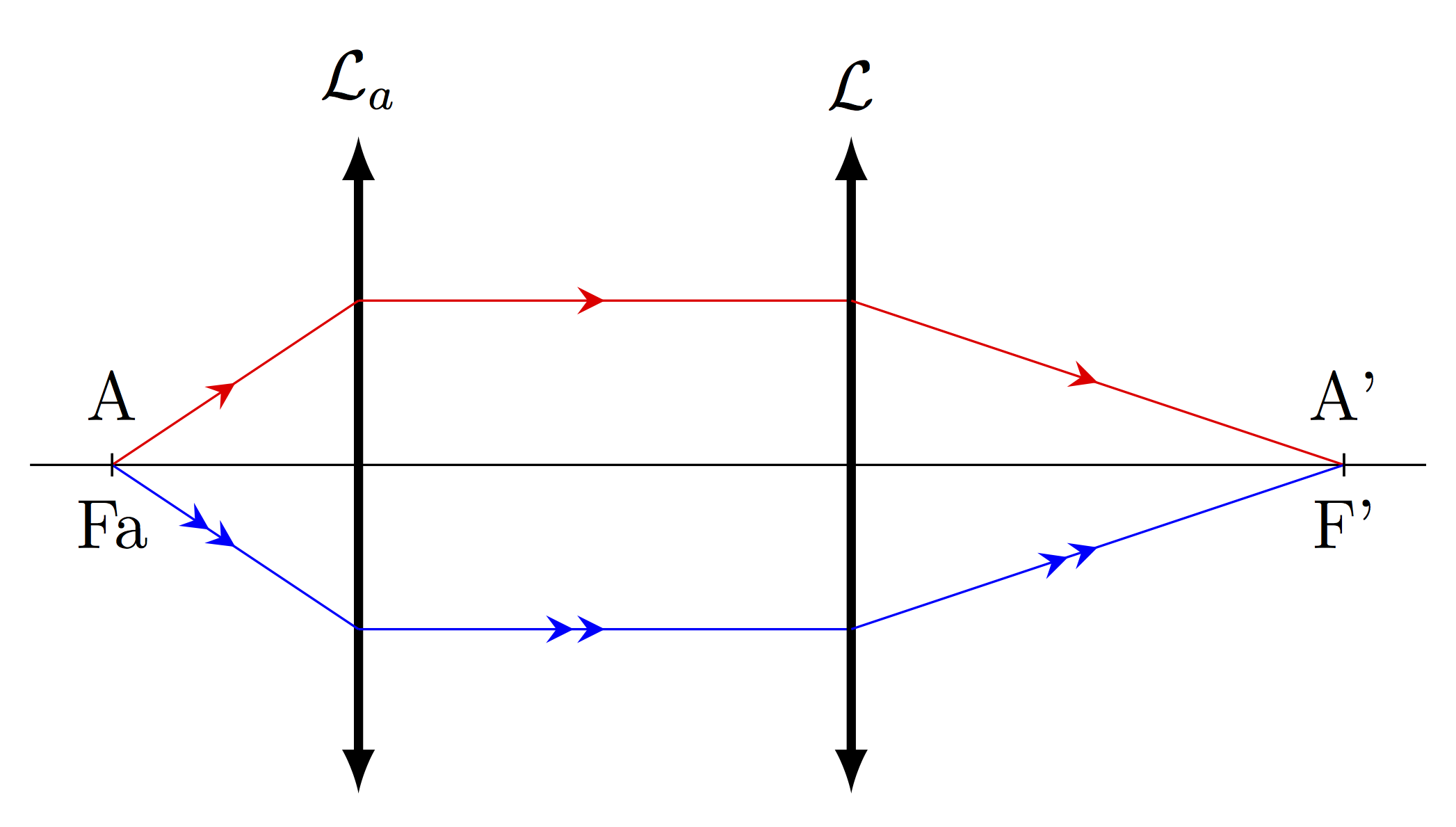
Principe
On utilise ici 2 lentilles : une lentille auxiliaire (\(\mathcal{L}_\text{a}\)), que vous choisirez et dont vous aurez déterminer la focale grâce à l’autocollimation, et la lentille (\(\mathcal{L}\)) à étudier.
Quand le faisceau de lumière émergent est parallèle, cela signifie que l’image est à l’infini. On peut alors utiliser cette image comme objet pour une autre lentille.
On fabrique un objet à l’infini dont on se sert pour la deuxième lentille, l’image finale est alors dans le plan focal image de cette deuxième lentille.
A préparer : d'après le descriptif ci-dessus, pouvez vous dire si cette méthode est plus précise ou moins précise que l’autocollimation ? Pour quelle(s) raison(s) ?
Manipulation
- Faire l’autocollimation avec (\(\mathcal{L}_\text{a}\)).
- Retirer le miroir : on a alors un faisceau de lumière parallèle.
- Placer sur ce faisceau la lentille (\(\mathcal{L}\)) et rechercher l’image en avançant ou en reculant l’écran.
- \(\spadesuit\) Mesurer \(f'\) (expliquer quelle mesure vous prenez) et évaluer l’incertitude \(U_f'\) (à 95%). Critiquer les résultats, comparez cette méthode à la précédente.
Méthode des points conjugués
On se place dans le cas d’un objet et d’une image réelle, la marche des rayons est celle de la figure ci-contre.
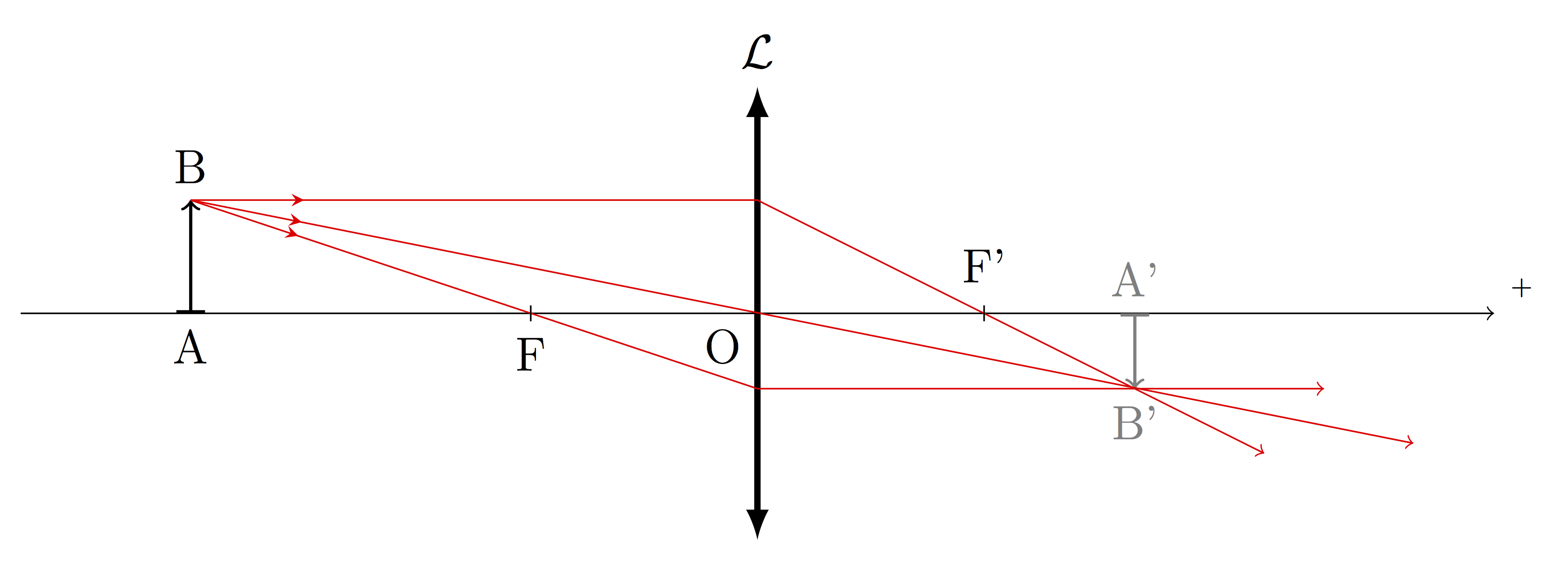
A préparer
D’après le schéma ci-dessus, faut-il raccourcir la distance OA ou l’augmenter pour obtenir une image A’B’ plus grosse que l’objet ? Complétez-le pour montrer cela. D’après vous, dans quelle configuration l’incertitude sera la plus petite, petite image ou grande image ?
- Placer l'objet à un bout du banc d'optique, l'écran à l'autre bout. Prendre pour \(\overline{OA}\), 2 valeurs différentes (remplir un tableau).
- Dans chaque cas :
- Chercher la position de l’image en déplaçant l'écran ;
- \(\spadesuit\) Déterminer expérimentalement les valeurs correspondantes de \(\overline{OA'}\) ;
- \(\spadesuit\) Évaluer les incertitudes (à un niveau de confiance de 95%) de mesures sur \(\overline{OA}\) (utiliser la graduation minimale du banc) et \(\overline{OA'}\) (évaluer la plage de valeurs acceptables = plage de netteté de l'image) ;
- \(\spadesuit\) Avec AB et A’B’, calculer le grandissement \(\gamma\), comparer à \(\dfrac{\overline{OA'}}{\overline{OA}}\) ;
- \(\spadesuit\) A partir de ces mesures, calculer \(f\)’ en utilisant la relation de conjugaison ;
- On prendra la formule suivante pour le calcul de l’incertitude (à 95%) \(U_f'\) :
\begin{equation}U_f’ = f’^2 \sqrt{\left(\dfrac{U_\overline{OA’}}{\overline{OA’}^2}\right)^2 + \left(\dfrac{U_\overline{OA}}{\overline{OA}^2}\right)^2}\end{equation} \(\spadesuit\) En déduire \(U_f'\) numériquement. Critiquer les résultats.
Méthode de Bessel
Principe
On note \(D\) la distance entre l'objet et l'écran sur lequel se formera une image, et \(f'\) la focale de la lentille étudiée. On peut montrer par le calcul que si \(D \geq 4\,f'\), alors il existe deux positions de lentille permettant d'obtenir une image à l'écran. Soit \(d\) la distance entre ces deux positions, on a alors : \begin{equation*} f' = \dfrac{D^2-d^2}{4\,D} \end{equation*}
A préparer : A l'aide de la formule aux dérivées partielles, préparer le calcul d’incertitude sur f’, sachant que l’on considère l’incertitude sur D négligeable devant l’incertitude sur d (\(U_D = 0\)). Montrer que \begin{equation*} U_{f'} = \dfrac{d \times U_d}{2\,D} \end{equation*}
Protocole
- Placer l'objet et l'écran aux deux extrémités du banc d'optique. Noter la distance \(D\).
- Placer la lentille à étudier au milieu du banc et rechercher les deux positions permettant d'avoir une image nette à l'écran. Noter \(d\) la distance séparant ces deux positions.
- En déduire la focale de la lentille et son incertitude à 95%.
Conclusion
\(\spadesuit\) Comparer la précision des quatres méthodes permettant d'obtenir la focale d'une lentille convergente.
Lentille divergente
Association de lentilles
Principe
On utilise dans cette méthode le fait que la vergence d’un système constitué de 2 lentilles minces accolées est la somme des vergences de chacune des 2 lentilles.
Manipulation
On recherche la focale de la lentille la moins divergente qui est à votre disposition.
- Associer une lentille convergente (de vergence connue ou déterminer par autocollimation) et une lentille divergente pour que l’ensemble soit convergent. Pour considérer que les lentilles sont accolées, il faut en tenir une à la main et la mettre contre l’autre lentille qui est sur pied.
- \(\spadesuit\) En utilisant la méthode d’autocollimation, déterminer la vergence du système et en déduire la distance focale de la lentille divergente et estimer son incertitude à 95%.
Méthode des points conjugués
Principe
Le seul cas où une lentille divergente fournit une image réelle est celui où l’objet est virtuel. On "fabrique" cet objet virtuel à l’aide d’une lentille convergente selon le schéma ci-dessous :
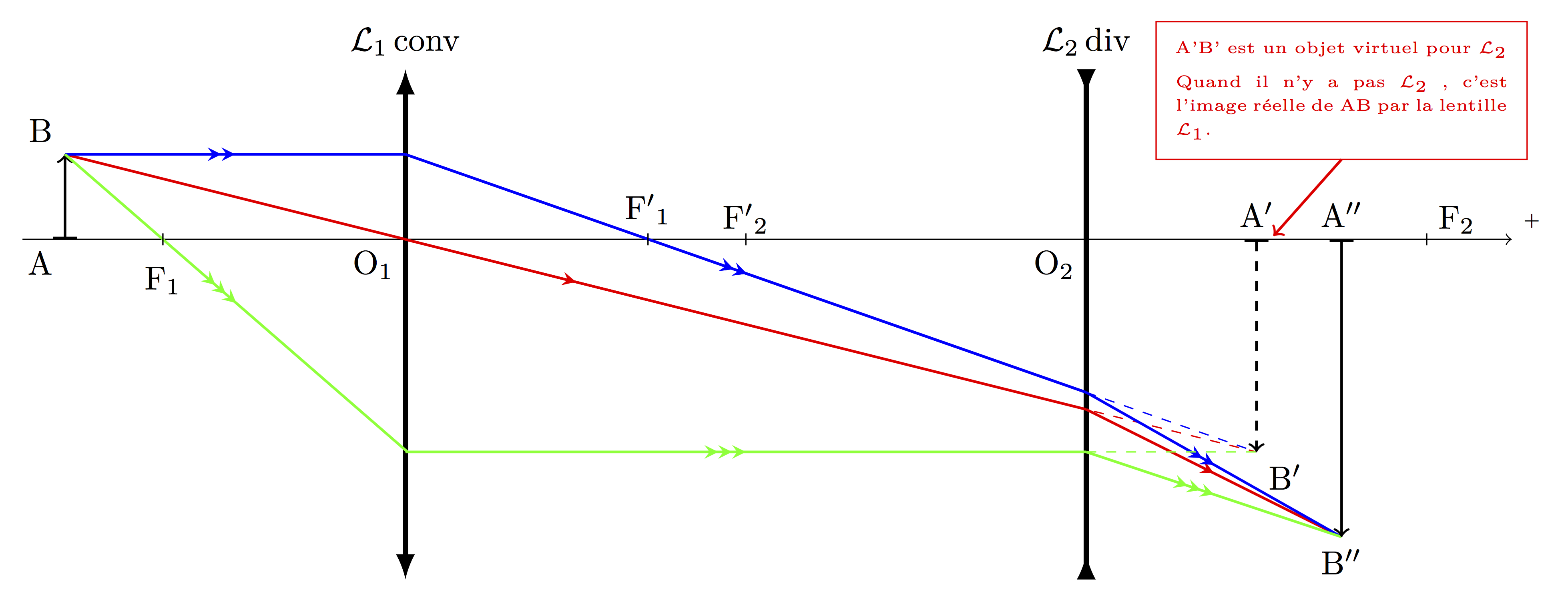
A’B’, image réelle obtenue par \(\mathcal{L}_1\), est située entre \(\mathrm{O_2}\) et \(\mathrm{F_2}\) et devient donc un objet virtuel pour \(\mathcal{L}_2\): l’image finale est A”B”, réelle. On placera la lentille divergente assez proche de l’écran qui recueille l’image intermédiaire A’B’.
Manipulation
Prendre la même lentille divergente que précédemment.
- \(\spadesuit\) Former une image réelle à l’aide d’une lentille convergente ;
- Placer la lentille divergente entre la lentille convergente et A’B’ (plutôt proche de A’B’). L'image sur l'écran devient floue. Noter la distance \(\mathrm{O_2A'}\).
- Éloigner l’écran pour retrouver une image nette (image finale A”B”). La zone de netteté peut être assez grande. L’important est d’avoir cette zone nette entre 2 flous. Changer les distances si ce n’est pas le cas.
- \(\spadesuit\) Noter la position \(\mathrm{O_2A”}\) et en déduire la distance focale de la lentille divergente à l’aide de la formule de conjugaison.
- On rappelle que la formule de calcul de l'incertitude sur \(f'\) par la méthode de conjugaison est:
\begin{equation}
U_f’ = f’^2 \sqrt{\left(\dfrac{U_\overline{OA’}}{\overline{OA’}^2}\right)^2 + \left(\dfrac{U_\overline{OA}}{\overline{OA}^2}\right)^2}
\end{equation}
Calculer l'incertitude à 95% sur cette mesure de focale. - Comparer cette valeur à celle obtenue précédemment.
Que mettre dans le fichier de résultats à poster ?
Pour rappel, vous devez déposer votre fichier ici à l'issue du TP. En PDF avec le nom du groupe (une lettre de groupe et un numéro de binôme).
- Vos résultats (mesure et incertitude) sur la mesure de la focale avec la méthode d'autocollimation.
- Vos résultats de mesures avec la méthode de l'objet à l'infini, un schéma qui montre les distance que vous avez utilisé entre les différentes lentilles. La comparaison de ces résultats avec ceux de la méthode précédente.
- Vos résultats de mesures pour la méthode des points conjugués. La comparaison de ces résultats avec ceux des deux méthodes précédentes.
- Vos résultats de mesures pour la méthode de Bessel. La comparaison de ces résultats avec ceux des trois méthodes précédentes.
- La lentille convergente que vous avez utilisée avec la lentille divergente pour former un doublet convergent.
- Les résultats (mesures et incertitudes) des deux méthodes de mesure de la focale d'une lentille divergente, et une comparaison de ceux-ci.
Annexe : liste de matériel
- Une lampe quartz-iode ;
- Une alimentation alternative 12V ;
- Un banc optique d'une longueur de deux mètres plus un ensemble de pieds adaptés (5 au moins) ;
- Un ensemble de lentilles convergentes de différentes focales identifiées avec des lettres sur supports adaptés au banc optique ;
- Un ensemble de lentilles divergentes de différentes focales identifiées avec des lettres sur supports adaptés au banc optique ;
- Un écran blanc pouvant se positionner sur un pied du banc optique ;
- Un support de diapositive pouvant se positionner sur un pied du banc optique ;
- Une diapositive objet transparente mais dépolie ;
- Un miroir









