TP-cours : circuit RLC en régime libre

Objectifs :

Etudier le circuit RLC libre c'est à dire la décharge d'un condensateur dans un dipôle bobine-conducteur ohmique ;
Découvrir l'existence de différents régimes, comment ils sont obtenus, quelles sont leurs caractéristiques ;
Etudier plus précisément le régime d'oscillations électriques, l'influence de certains paramètres sur ces oscillations.

Décharge d'un condensateur dans un ensemble bobine-conducteur ohmique

Visionnez la vidéo ci-dessous, elle traite du problème théorique du circuit RLC en régime libre, notamment en présentant l'analogie électromécanique qui rapproche le circuit RLC d'un problème de solide-ressort avec frottements.

Téléchargez ici le pdf support de cette vidéo

Réalisation du montage

Rendez-vous à l'adresse http://www.multisim.com et construisez un circuit RLC série avec les composants suivants :

$C = 0,1\,\mathrm{\mu\,F}$ ;
$L = 1\,\mathrm{H}$ ;
$R = 100\,\Omega$ ;

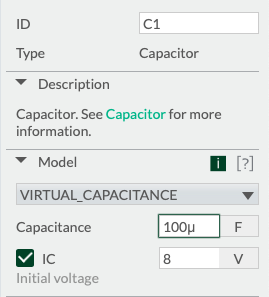
Comme nous voulons simuler la décharge du condensateur dans les autres dipôles du circuit, il faut indiquer au logiciel que celui-ci est préalablement chargé. Il faut donc rentrer une valeur de tension pour le condensateur chargé.

Et dire au logiciel de prendre en compte la valeur initial des composants :

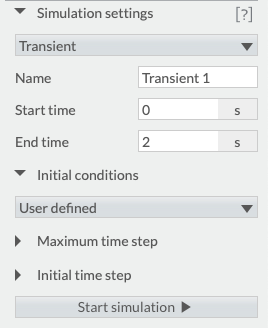
Existence de différents régimes : influence de la résistance du conducteur ohmique

Simulation

Réglez le logiciel pour observer la tension aux bornes du condensateur.
Réglez la valeur du temps d'acquisition : dans "Simulation settings" on règlera le "End time" à la valeur $0,015\,\mathrm{s}$.
Observez et notez l’allure de la courbe $u_C(t)$ pour les différentes valeurs de la résistance $R$ suivantes :
$R = 100\,;\,1 000\,;\,3 000\,;\,6 000\;\text{et}\;10\,000\,\Omega$.

Question

Dans un tableau, rassemblez les valeurs de $R$, nommez le régime obtenu et donnez la valeur de $Q$, facteur de qualité du montage.

Etude du régime pseudo-périodique

Pseudo-période et période propre, différences

Soit les oscillations électriques obtenues pour $C = 0,1\,\mathrm{\mu\,F}$, $L = 1\,\mathrm{H}$ et $R = 100\,\Omega$.

Rappelez pourquoi on parle de pseudo-période plutôt que de période dans le cas de ces oscillations.
Mesurez la pseudo-période obtenue. Comparez-la à la période propre du circuit et concluez (vous pouvez calculer la période propre, ou l'obtenir par simulation).

Influence de $R$

La valeur de la résistance du conducteur ohmique influe t-elle sur la pseudo-période des oscillations électriques ? si oui, qualifier (avec un adjectif) cette influence.
Est-ce en accord avec la théorie ? expliquez.

Influence de $L$

Pour des paramètres $C = 0,1\,\mathrm{\mu\,F}$ et $R = 100\,\Omega$, faites varier l'inductance $L$ de la bobine selon le tableau ci-dessous et notez les valeurs de la pseudo-période $T$ :

$L$ (H)	1,2	1,0	0,8	0,6	0,4
$T$ (s)

Concluez : y a-t-il accord avec la théorie ? expliquez.

Influence de $C$

Pour des paramètres $L = 1\,\mathrm{H}$ et $R = 100\,\Omega$, faites varier la capacité $C$ du condensateur selon le tableau ci-dessous et notez les valeurs de la pseudo-période $T$ :

$C\,$($\mathrm{\mu\,F}$)	0,1	0,5	1,0	1,5	2,0
$T$ (s)

Concluez : y a-t-il accord avec la théorie ? expliquez.

Etude du régime critique

A l'aide de la simulation, pour $C = 0,1\,\mathrm{\mu\,F}$ et $L = 1\,\mathrm{H}$, trouvez le régime critique.
Notez la résistance critique, calculer le facteur de qualité. Comparer-le avec celui attendu théoriquement.
Retrouvez le en utilisant le fait que, pour le régime critique : \begin{equation*} \text{à}\,t=\dfrac{1}{\lambda},\, u_C = 2\,E\,e^{-1} \end{equation*} où $E$ est la tension initiale aux bornes du condensateur.

Exercice : circuit LC série réel

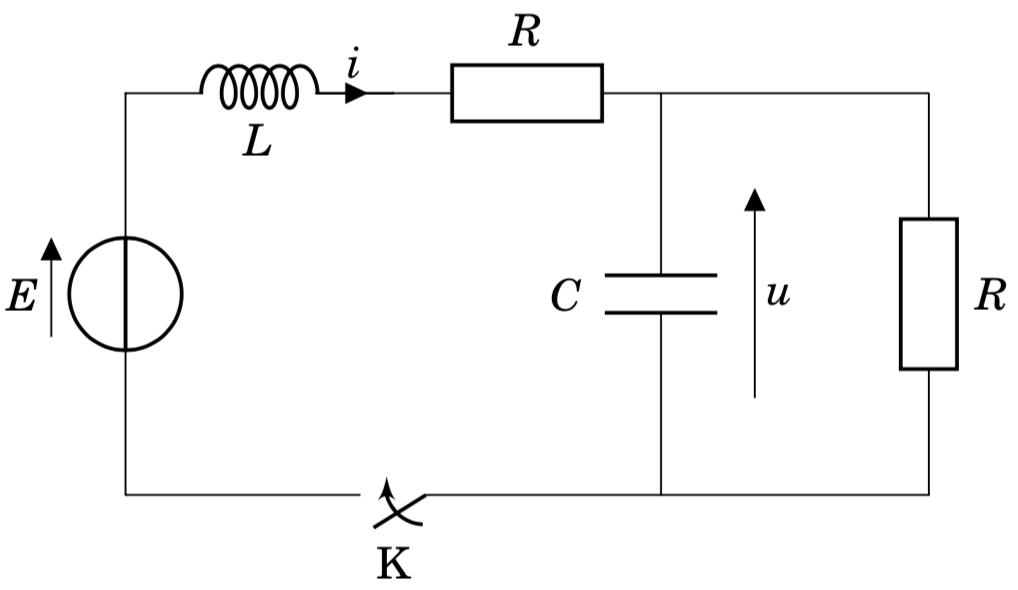
Étudions un circuit LC réel composé d'une bobine d'inductance $L$ en série avec un conducteur ohmique de résistance $R$, suivi d'un condensateur de capacité $C$ en parallèle avec un conducteur ohmique de résistance $R$. On suppose que les deux résistances ont même valeur et que $\tau = \dfrac{L}{R} = RC$. Le condensateur est initialement déchargé.

Etablir l'expression de $u(t)$ pendant le régime transitoire. L'instant initial $t=0$ correspond à la fermeture de l'interrupteur K.

Indications : il faut d'abord écrire la loi des noeuds au niveau du condensateur et de la résistance en parallèle afin d'obtenir l'expression d l'intensité $i$ du courant. Ensuite on fait la loi des mailles dans la branche principale.
Vous devez trouver l'équation différentielle suivante:
\begin{equation}\dfrac{d^2u}{dt^2} + \dfrac{2}{\tau}\dfrac{du}{dt} + \dfrac{2}{\tau^2}u = \dfrac{E}{\tau^2}\end{equation} Il faut ensuite la résoudre complètement, avec les conditions initiales.
Donner, sans calcul, l'expression de la tension $u$ aux bornes du condensateur et de l'intensité $i$ dans le circuit en régime permanent.
Pour cela, redessiner le circuit en considérant le comportement du condensateur et de la bobine dans ce type de régime.