TP magnétisme

Pour avoir le temps de faire la deuxième partie, ne pas passer trop de temps sur la première.

Notion de champ magnétique

Définition et exemples

Un champ est une grandeur scalaire ou vectoriel dont la valeur et/ou l’orientation dépend de l’endroit de l’espace. Deux exemples typiques :

• Le champ de température est un champ scalaire : à chaque point de l’espace (ou d’une surface) est associée une valeur de température ;
• Le champ des vents est un champ vectoriel : à chaque point de l’espace (ou d’une surface) est associée une valeur de vent et sa direction.

Détection d’un champ

Un champ peut régner dans un espace sans que l’on s’en rende compte : pour le détecter, on utilise un dispositif qui produit une certaine réponse en présence de ce champ. Par exemple, en présence du champ de pesanteur terrestre, un système masse-ressort vertical s'allonge d'autant plus que le champ de pesanteur est important.

Champ magnétique et détection

On s'intéresse ici au champ magnétique produit par les aimants et les courants électriques. Il s'agit d'un champ vectoriel dont la direction est donnée par une aiguille aimantée (alignement sud-nord) et dont l'intensité est obtenue à l'aide d'une sonde à effet Hall.

Dans le système international d'unités, le champ magnétique s'exprime en tesla (symbole : T) en hommage au physicien Nikola Tesla.

La Terre crée elle-même un champ magnétique appelé champ magnétique terrestre. Ce sont des courants de convection de matière chargée dans le manteau terrestre qui créent ce champ. En un point de la surface de la Terre, la direction du champ terrestre est inclinée vers le sol : on décompose le champ magnétique terrestre en une composante horizontale et une composante verticale. Dans ce TP, on considèrera uniquement sa composante horizontale.

Détermination du champ magnétique terrestre

Champ créé par une spire

Une spire de rayon \(R\) parcourue par un courant \(I\) créé un champ magnétique dans tout l'espace. Si l'on se place au centre de la spire, alors le champ magnétique présente les caractéristiques suivantes.

• Intensité : \[ B = \dfrac{ \mu_0\,I}{2R} \] avec \(\mu_0 = 4 \pi \times 10^{-7}\) SI une constante appelée perméabilité du vide.
• Direction : suivant l'axe de la spire.
• Sens : donné par la règle du tire-bouchon.

Pour \(N\) spires jointives (collées les unes aux autres) formant une spire d'épaisseur négligeable on peut utiliser le résultat précédent à condition de remplacer \(I\) par \(NI\) : \begin{equation}\boxed{B = \dfrac{\mu_0\, N \, I}{2R}}\end{equation}

Principe de la mesure

Le champ magnétique ambiant est le résultat du champ magnétique terrestre (environ 10^-5 T) et des sources électriques inévitables qui créent également des champs magnétiques non négligeables. On notera \(\overrightarrow{B}_\mathrm{a}\) la composante horizontale de tous ces champs.

On commencera par placer une boussole au centre O d'une spire alors que celle-ci n'est parcourue par aucun courant. Le pole nord de la boussole indique alors la direction de \(\overrightarrow{B}_a\) (schéma ci-contre). Cette position correspond à une déviation nulle de la boussole (\(\alpha=0\)).

On positionne la spire de façon à ce que son axe soit perpendiculaire à \(\overrightarrow{B}_a\). Lorsqu’un courant \(I\) circule dans la spire, elle crée un champ magnétique \(\overrightarrow{B}\) qui vient s’ajouter vectoriellement au champ \(\overrightarrow{B}_\mathrm{a}\). Il en résulte un champ \(\overrightarrow{B}_\mathrm{T}\) qui fait un angle \(\alpha\) avec la position initiale de la boussole. Les champs \(\overrightarrow{B}_\mathrm{a}\) et \(\overrightarrow{B}\) formant un angle droit, on peut écrire : \[ \tan \alpha = \dfrac{B}{B_\mathrm{a}} \]

Cette angle est mesurable sur l’échelle graduée circulairement au centre de la spire. Comme \(B = \dfrac{\mu_0\, N \, I}{2R}\) alors \begin{equation}\boxed{\tan \alpha = \dfrac{\mu_0\, N \, I}{2RB_a}}\label{eq:boussole_des_tangentes}\end{equation} L’angle \(\alpha\) est fonction de \(N\) (nombre de spires), \(I\) (intensité du courant dans la spire) et \(R\) (rayon de la spire). Nous allons vérifier ceci.

Description du matériel, précautions

• Toutes les spires sont constituées par un dépôt (formant des cercles) de métal conducteur sur une plaque d’isolant. Des bornes percées dans cette plaque permettent de faire passer du courant dans les spires : les fils d’alimentation venant du générateur viendront se brancher sur une même colonne de bornes de la spire: la colonne de droite permettra de travailler avec une seule spire de rayon variable, la colonne de gauche de travailler avec plusieurs spires dont on prend un rayon moyen.
  
  
• Pour le générateur de courant, on utilise une alimentation stabilisée de courant maximum 10 A. Dans tous les cas, faire attention aux valeurs des courants limites indiquées sur l’appareil et sur la plaque.
• On mesurera le courant \(I\) avec un ampèremètre (multimètre) en série : attention au calibre (on utilisera le calibre 10A). Aux cours des mesures, ne pas rester trop longtemps avec \(I > 1\, A\).
• Pour faire le zéro de la boussole, on procédera ainsi : on place une boussole sur pivot au centre de la spire et on attend l'équilibre mécanique. On aligne ensuite la direction sud-nord avec le zéro de la graduation angulaire. On ne modifiera plus ce réglage (la plaque contenant les spires ne doit plus être déplacée).

• Il faut effectuer chaque mesure à plusieurs reprises : lorsque l’aiguille semble avoir pris sa position d’équilibre, la déplacer manuellement et attendre qu’elle revienne dans sa position d’équilibre. Noter alors l’angle obtenu. Recommencer en déplaçant l’aiguille dans l’autre sens. Noter à nouveau l’angle … Retenir la valeur qui semble être la plus reproductible, ou la moyenne des valeurs obtenues (prendre des initiatives) … Le but de ces mesures répétées est de compenser les frottements de l’aiguille sur son axe.

Mesures et exploitation

Étude du champ magnétique en fonction du rayon de la spire

1. \(\spadesuit\) Pour les 4 spires de rayons différents, mesurer \(\alpha\) avec \(I = 1 \mathrm{A}\). Remplir, dans Regressi™, un tableau de valeurs comportant \(R\), \(\alpha\) et \(\tan \alpha\) (attention aux unités).
2. Evaluer l’incertitude sur la lecture de l’angle (plage de valeurs acceptables) puis l’entrer dans la colonne appropriée sous Regressi™. L’incertitude sur le rayon \(R\) sera prise nulle, mais il faudra néanmoins la renseigner.
3. \(\spadesuit\) Tracer la courbe \(\tan \alpha = f(\frac{1}{R})\). Faites apparaître les ellipses d'incertitude.
4. \(\spadesuit\) Choisir le modèle théorique adéquat qu'il faut ajuster aux mesures. La loi \eqref{eq:boussole_des_tangentes} est-elle vérifiée ? En déduire une valeur expérimentale de \(B_\mathrm{a}\) et son incertitude.

Étude du champ magnétique en fonction de l’intensité du courant dans plusieurs spires

Dans la manipulation suivante, on travaillera avec les mêmes préoccupations pour les incertitudes. A l’incertitude sur l’angle, on ajoutera celle sur l’intensité mesurée sachant que la notice de l'ampèremètre indique une précision \(\Delta_c =\pm(1{,}5\%I + 0{,}1\,\mathrm{mA})\).

1. \(\spadesuit\) Pour le groupe de 5 spires (noter le rayon moyen indiqué sur la plaque), mesurer \(\alpha\) pour 8 valeurs du courant \(I\). Remplir un tableau comportant \(I\), \(\alpha\) et \(\tan \alpha\). Ne pas dépasser \(2{,}5\,\mathrm{A}\).
2. \(\spadesuit\) Porter \(\tan \alpha\) en fonction de \(I\) puis procéder comme précédemment. En déduire une valeur expérimentale de \(B_\mathrm{a}\) et son incertitude.
3. Commenter vos résultats.

★ Ne pas oublier d'imprimer les courbes correctement annotées ★

Champ créé par une bobine

Les mesures se font ici avec un teslamètre et sa sonde (teslamètre Leybold ou Jeulin): attention, le teslamètre n’est pas dans le circuit électrique !

La sonde du teslamètre est un capteur de Hall, sensible aux champs perpendiculaires à la tige si la sonde est "tangentielle" (position "\(B_z\)") et aux champs parallèles à la tige si la sonde est axiale (position "\(B_x\)"). Regarder les indications fléchées sur la sonde.

Théorie

Soit une bobine circulaire de rayon \(R\) et de largeur \(L\). Le bobinage est réparti uniformément en plusieurs couches et le nombre de spires est \(N\). Les spires sont parcourues par le courant \(I\).

Champ au centre : le champ magnétique au centre est donné par \begin{equation} B_\text{theo}(\text{O}) = \dfrac{\mu_0\,N\,I}{2} \dfrac{1}{\sqrt{R^2+\left(\dfrac{L}{2}\right)^2}} \end{equation}

Champ sur l’axe : sur l’axe Ox (voir schéma précédent), le champ pour une bobine fine est donné par \begin{equation} B_{\text{theo}}(\text{M}) = B_\text{theo}(\text{O})\, \sin^3 \, \theta \end{equation} avec \[\sin\,\theta = \dfrac{R}{\sqrt{R^2+x^2}}\]

Montage expérimental

On étudie ici une des deux bobines du dispositif de Helmholtz. On donne : \[ N = 100\,\mathrm{spires}\quad 2R = 125\,\mathrm{mm} \quad\text{et}\quad L = 34\,\mathrm{mm} \]

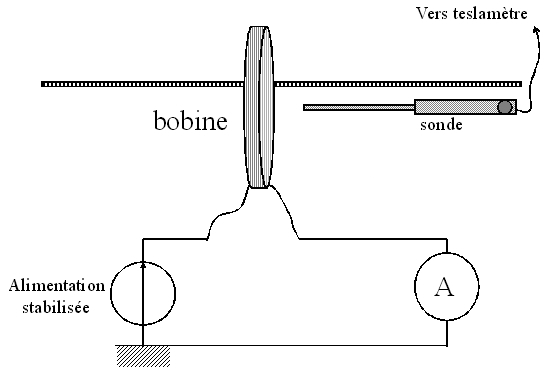
On réalise un circuit en série composé de l’alimentation stabilisée, la bobine fine et un ampèremètre. On placera un interrupteur (non indiqué sur le schéma ci-dessous) dans le circuit.

La sonde du teslamètre sera placée de façon à mesurer le champ magnétique qui règne sur l'axe de la bobine (position "\(B_x\)"). La partie utile de la sonde qui doit être positionnée au centre de la bobine est identifiée sur la photo ci-contre.

La mesure du champ magnétique se fait en deux temps.

• Ouvrir le circuit à l'aide de l'interrupteur puis lire la valeur \(B_0\) indiquée par le teslamètre. Si le zéro est fait, l'appareil indique 0 mT.
• Fermer le circuit puis lire la valeur \(B_1\) indiquée. La valeur du champ magnétique vaut alors \(B=B_1-B_0\)

Mesures et exploitation

Champ au centre

1. Fermer le circuit et régler l’intensité \(I\) parcourant la bobine à \(2\,\mathrm{A}\).
2. Positionner la sonde de façon à ce qu’elle soit bien au centre de la bobine : le champ magnétique créé par celle-ci est maximum lorsque \(x\) vaut 0, il est minimum quand \(y\) vaut 0.
3. \(\spadesuit\) Mesurer la valeur du champ magnétique donné par le teslamètre en millitesla (mT).
4. \(\spadesuit\) A l’aide des données de \(L\) et \(R\), calculer le champ magnétique théorique au centre de la bobine fine. On rappelle : \(\mu_0 = 4\,\pi\,\times 10^{-7}\,\mathrm{SI}\).
5. Conclure, sachant que la notice du teslamètre indique une tolérace égale à ±(3% valeur lue + 30 µT)

Champ sur l’axe

1. Régler l’intensité \(I\) à \(2\,\mathrm{A}\).
2. \(\spadesuit\) Mesurer le champ \(B_{\mathrm{exp}}\) pour différentes valeurs de \(x\) compris entre \(0\) et \(20\,\mathrm{cm}\). Remplir un tableau comportant \(x\) et \(B_{\mathrm{exp}}\).
3. \(\spadesuit\) Créer la grandeur \(X=\sin^3\theta\) puis porter \(B_\text{exp}\) en fonction de \(X\).
4. \(\spadesuit\) Choisir le modèle théorique adéquat qu'il faut ajuster aux mesures. Discuter la cohérence des résultats.

★ Ne pas oublier d'imprimer les courbes correctement annotées ★

Bobines de Helmholtz

Théorie

2 bobines fines de rayon \(R\), espacées de \(R\), parcourues par un courant \(I\) dans le même sens constituent un ensemble appelé bobines de Helmholtz.

Le champ magnétique créé sur l'axe du système est le résultat de la somme des champs magnétiques produits par chaque bobine plate. Si l'on place l'origine des abscisses en O₁, on trouve : \[ B = \frac{\mu_0NI\,R^2}{2} \left[\frac{1}{\left(R^2+x^2\right)^{3/2}} + \frac{1}{\left(R^2+(x-R)^2\right)^{3/2}}\right] \]

Dans cette formule $N$ représente le nombre de spires d'une bobine.

L'intérêt de ce montage est d'obtenir un champ magnétique constant entre les bobines, on peut alors, avec des bobines de grandes dimensions, faire des expériences à champ magnétique constant (voir mesure du rapport $e/m$ de l'électron). On peut voir ces bobines comme un "condensateur magnétique", le champ est constant entre les "armatures".

Manipulation

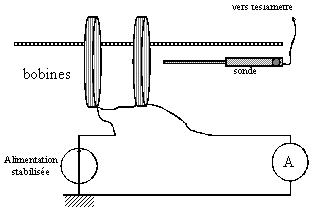
Montage

On place la deuxième bobine fine dans son support de manière à ce que la distance entre les deux bobines soit \(R\). Les deux bobines doivent être en série et le courant \(I\) dans le même sens dans les 2 bobines. On peut vérifier cela en mesurant \(B\) qui doit être maximum au milieu et sur l’axe des deux bobines.

Mesures

1. Régler l’intensité du courant à \(2\,\mathrm{A}\) et vérifier le zéro du teslamètre.
2. \(\spadesuit\) Mesurer le champ \(B_{\mathrm{exp}}\) pour pour \(x =0\,\mathrm{cm}\) (origine des abscisse en $\mathrm{O_1}$) jusqu’à \(x = 20\,\mathrm{cm}\). Remplir un tableau de mesures.
3. \(\spadesuit\) Représenter sous Regressi™ la courbe \(B=f(x)\). Commenter.
4. \(\spadesuit\) Ajouter dans votre fichier Regressi la grandeur calculée suivante (faites un copier/coller depuis le texte du site internet):
   Btheo = 4*pi*1e-7*100*0.0625^2*((1/(0.0625^2+x^2)^(3/2))+(1/(0.0625^2+(x-0.0625)^2)^(3/2)))
   
   Superposer la courbe \(B_{\mathrm{theo}}=f(x)\) avec votre courbe \(B_{\mathrm{exp}}=f(x)\). Conclure.
5. \(\spadesuit\) Mesurer \(B\) pour \(x=R/2\) puis calculer la valeur théorique. Comparer et discuter.

★ Ne pas oublier d'imprimer les courbes correctement annotées ★