TP Thermodynamique

Hydrostatique

Théorie

On considère un récipient contenant un liquide (de l'eau) de masse volumique \(\rho_2\). On mesure la pression à la profondeur \(\ell\) à l'aide d'une sonde de pression branchée à un manomètre à liquide. Ce dernier est constitué d'un tube en U, rempli d'un liquide (masse volumique \(\rho_1\)) et relié à une sonde par un tuyau étanche. La colonne d'air située dans le raccord est à la même pression que l'air piégé dans la sonde.

Dans un liquide au repos, la pression \(p\) augmente proportionnellement à la profondeur \(h\) via la loi \begin{equation} \boxed{ \displaystyle{ p=p_\text{surface}+\rho gh }} \quad \heartsuit \label{tp_thermodynamique_eq1} \end{equation} où \(\rho\) est la masse volumique du liquide, \(p_\text{surface}\) sa pression à la surface, et \(g\) le champ de pesanteur.

Manipulation

Avant de commencer, vérifier que lorsque la sonde est hors de l'eau, la dénivellation indiquée par le manomètre est correcte. Eventuellement, mettre en contact l'air du raccord avec l'air extérieur pour faire le zéro (en ouvrant la pince).

1. En haut du dispositif une petite molette permet de pivoter la sonde. Plonger la sonde dans l'eau ouverture vers le bas
2. \(\spadesuit\) Pour différentes profondeurs \(\ell\) de la sonde, mesurer la dénivellation \(h\) du manomètre.
3. Rentrer les mesures dans un tableau Regressi™. Ajouter y les incertitudes (écart-types) de mesure. Proposer une modélisation théorique.
4. \(\spadesuit\) Les résultats sont-ils en accord avec les considérations théoriques précédentes ? Selon vous, quel est le liquide présent dans le manomètre ?
5. \(\spadesuit\) Imprimer le tableau de mesures et les courbes correctement annotées.

Loi des gaz parfaits

Loi de Mariotte

On cherche à vérifier la loi de Mariotte qui stipule que pour un gaz parfait maintenu à température constante, le produit de sa pression par son volume reste constant : \begin{equation} \boxed{pV_{\mathrm{TOT}}=\mathrm{C^{te}}} \quad \heartsuit \label{tp_thermodynamique_eq2} \end{equation}

Pour cela on utilise une seringue munie d'un capteur de pression et de température. La seringue peut être fermée par un bouchon ou un piston mobile.

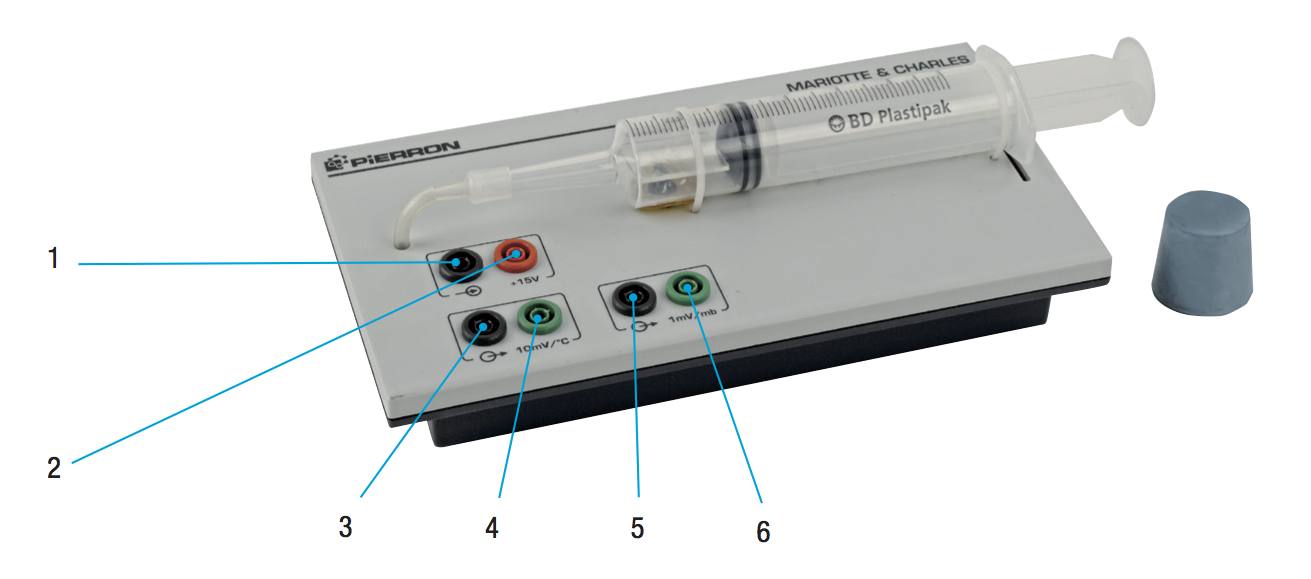
Réglages :
• Si vous avez le matériel de la Fig. 4: alimenter l’appareil en +15 V continus (bornes 1 et 2). Ensuite, connecter un voltmètre sur les bornes 5 et 6 : la tension (= DC) indiquée est proportionnelle à la pression de l'air contenue dans la seringue, sachant que 1 mV correspond à 1 mbar.
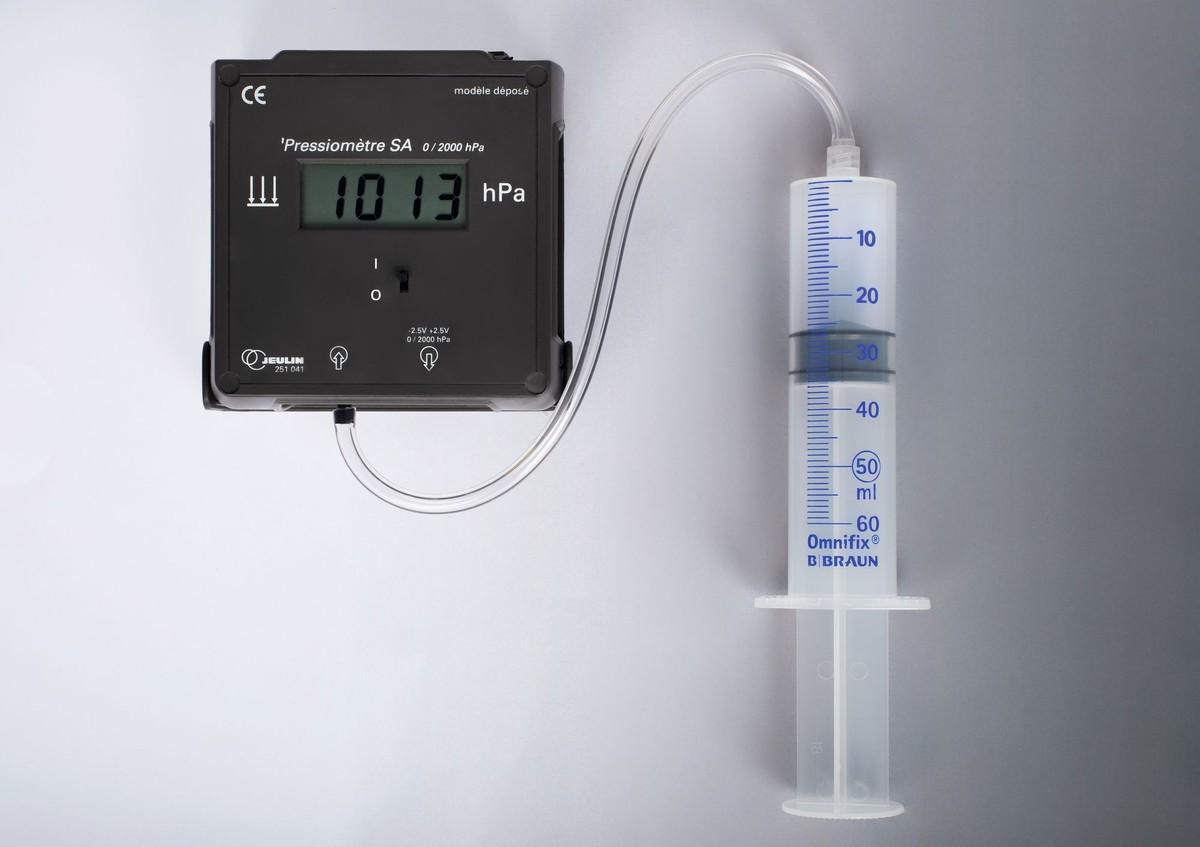
• Pour le matériel de la Fig. 5: aucun réglage nécessaire.

Manipulation : Fermer la seringue à l'aide du piston puis obturer l'autre extrémité à l'aide du raccord silicone. On note \(V\) le volume d’air indiquée sur la seringue et \(V_0\) le volume d’air à l’intérieur du tube flexible qui relie la seringue au capteur de pression. \(V_0\) est inconnu mais constant.

1. À partir d'une position enfoncée du piston, tirer dessus pour augmenter progressivement le volume \(V\). Relever dans un tableau Regressi le volume \(V\) et la tension du capteur de pression.
2. Ajouter les incertitudes (écart-types) de mesure. Pour la pression, on prendra une précision constructeur\(\Delta_c =4\,\mathrm{mV}\) (matériel de la Fig. 4). Pour la matériel de la Fig. 5, $\Delta_c = 2\%\,L \pm 4\,\mathrm{hPa}$
3. Créer les grandeurs \(p\) et \(x=1/p\) puis porter \(V\) en fonction de \(x\).
4. \(\spadesuit\) À partir de la loi de Mariotte, établir la relation entre \(V\), \(p\), \(V_0\). Proposer alors une modélisation dans Regressi™. Conclure (loi vérifiée?).
5. \(\spadesuit\) Déduire de la modélisation, la valeur du volume \(V_0\) (ne pas oublier l'unité et l'incertitude).
6. \(\spadesuit\) Imprimer le tableau de mesures et les courbes correctement annotées.

Détermination du zéro absolu

Lorsqu'un gaz parfait de volume fixé, est chauffée, sa pression augmente. Elle suit la loi de Charles : \begin{equation} p=\mathrm{C^{te}}(t-t_0) \label{tp_thermodynamique_eq3} \end{equation} où \(t\) est la température en degré Celsius (°C) et \(t_0\) la température du zéro absolu, c'est-à-dire la température correspondant à une pression nulle : les molécules sont alors complètement figées.

Pour déterminer le zéro absolu, on utilise une boule creuse de volume fixe, munie d'un manomètre pour mesurer la pression de l'air situé à l'intérieur. En plongeant la boule dans un bain d'eau tempérée, on peut mesurer l'évolution de la pression avec la température de l'air et vérifier ainsi la loi de Charles.

1. Remplir un cristallisoir avec de l'eau et le placer sur une plaque chauffante. Installer la boule de Joly dans le cristallisoir, puis plonger une sonde thermique. Ajouter un peu de glace de façon à obtenir de l'eau froide (≈10°C). Une fois l'équilibre atteint, relever la température et la pression.
2. Allumer la plaque chauffante (température de consigne sur 100°C). Relever la température et la pression à chaque fois que la pression augmente de 10 hPa. Tracer la température \(t\) en fonction de la pression \(p\). Pour la température on prendra \(u_t=0{,}1\mathrm{°C}\).
3. \(\spadesuit\) À l'aide d'une modélisation, vérifier la loi \eqref{tp_thermodynamique_eq3}. En déduire la température correspondant au zéro absolu. Discuter.
4. \(\spadesuit\) Imprimer le tableau de mesures et les courbes correctement annotées.

Azote liquide : effets des basses températures

Effet du froid sur les gaz : ballon de baudruche

Mettre un ballon de baudruche gonflé dans un cristallisoir, verser un peu d’azote liquide dessus (pendant quelques secondes).

\(\spadesuit\) Observer puis expliquer.

Caléfaction de l'azote liquide

Renverser un peu d'azote liquide sur la paillasse puis observer la présence de quelques gouttelettes glissant quasiment sans frottement avant de disparaître.

\(\spadesuit\) Interpréter.

Contact entre de l’azote liquide et de l’eau liquide

Remplir un petit bêcher au tiers d’eau puis verser un peu d’azote liquide.

\(\spadesuit\) De quoi est constitué le nuage que l’on voit "s’écouler" pendant l’expérience ? A quelle température environ peut-il être ? Qu’obtient-on à la fin de l’expérience ? Expliquer.

Moteur de Stirling

Inventé en 1816 (brevet déposé) par le pasteur et ingénieur Robert Stirling, ce moteur permet de transformer de l'énergie thermique en énergie mécanique à l'instar du moteur à explosion. Mais contrairement à ce dernier, le moteur Stirling utilise un fluide (ici : l’air) contenu dans une enceinte fermée, chauffé par une source de chaleur extérieure à l’enceinte. C’est donc un moteur à combustion externe, avec de nombreux avantages : combustion en continu, plus complète, pas de soupapes d’admission et d’échappement, donc moins de bruit, et possibilité (théorique) d’utiliser tout combustible solide, liquide, gazeux, solaire, nucléaire! D’où des prototypes pour la production d’électricité, l’irrigation et le dessalement de l’eau.

Ses principaux avantages sont :
• le silence de fonctionnement ;
• le rendement élevé ;
• les nombreuses sources chaudes possibles.

Ses principaux inconvénients sont :
• le prix ;
• la variété des modèles possibles, ce qui empêche la standardisation ;
• les problèmes d’étanchéité si l’on souhaite des pressions de fonctionnement élevées ;
• son manque de souplesse puisqu’il "préfère" fonctionner à régime constant (gros inconvénient pour l’industrie automobile).
  Source : http ://www.moteurstirling.com

Description

La maquette du moteur de Stirling est constitué d'un bac pour recevoir un brûleur à alcool (6), lequel fera office de source thermique. Un fluide (de l'air ici) est enfermé dans une enceinte hermétique et subit différentes transformations thermodynamiques. Cette machine consiste essentiellement en un cylindre de travail dans lequel deux pistons (8 et 11) exécutent des mouvements déphasés de \(\pi/2\). Le piston de travail (11) met en mouvement un volant (1) lequel est relié, via une courroie, à un générateur électrique permettant de convertir l'énergie mécanique en énergie électrique.

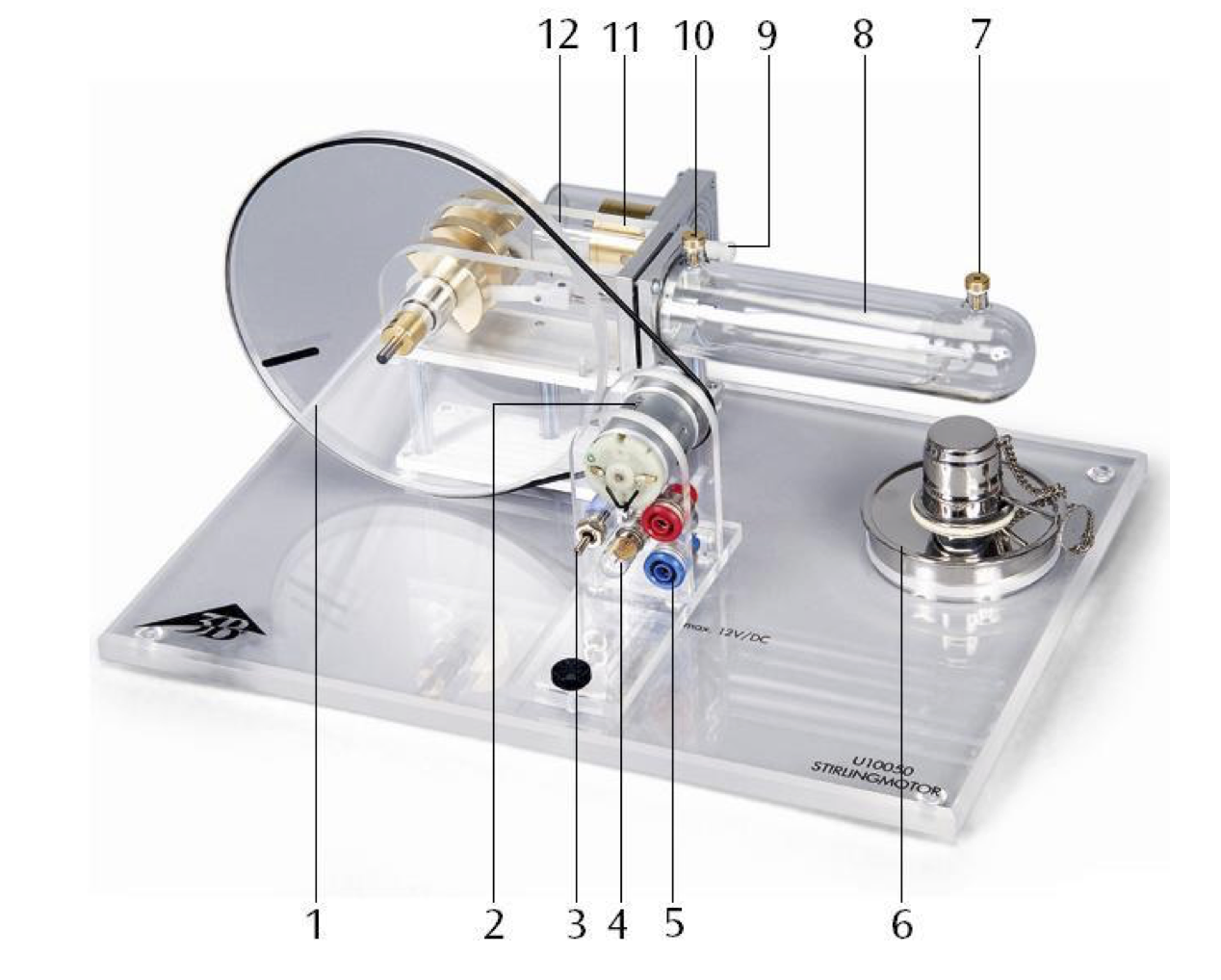
Le cycle de Stirling idéal comprend 4 phases :

1. phase d'expansion : l'air se détend à température constante (source chaude) ;
2. l'air refroidit à volume constant dans le régénérateur ;
3. l'air est ensuite comprimé de façon isotherme (source froide) ;
4. Enfin l'air est de nouveau réchauffé dans le régénérateur en passant dans le cylindre chauffé par le brûleur.

Ci-contre, le diagramme p-V correspondant.

Manipulations

Etude du moteur en charge

L’énergie mécanique fournie par le moteur est convertie en électricité par la génératrice.

1. \(\spadesuit\) Pendant que le moteur tourne, brancher une ampoule aux bornes de la génératrice. Que se passe-t-il ? Débrancher l’ampoule, que se passe-t-il ?
2. \(\spadesuit\) Remplacer l’ampoule par une DEL et faire la même manipulation. Conclure.

Quelques mesures

1. \(\spadesuit\) Mesurer la tension à vide (sans ampoule) aux bornes de la génératrice : pour cela, placer le voltmètre directement aux bornes de la génératrice.
2. \(\spadesuit\) Mesurer le courant de court-circuit : pour cela, brancher directement l’ampèremètre aux bornes de la génératrice.
3. \(\spadesuit\) Estimer la puissance électrique que peut délivrer le moteur. Commenter sa valeur.