Expériences de thermodynamique

Responsable : J. Roussel

L'expérience de Clément-Desormes

Description

Un peu d'histoire — En 1819, Nicolas Clément et Charles Desormes (son beau-père) conçoivent une expérience thermodynamique permettant la mesure du coefficient calorimétrique \(\gamma=c_p/c_v\) de l'air à la température ambiante. Par cette expérience, ils furent les premiers à mettre en évidence la loi de Laplace. De nos jours, elle présente surtout un intérêt pédagogique, car sa précision est médiocre. Les méthodes reposant sur la détermination de la vitesse du son (cf. TP 11) sont beaucoup plus précises.

Description du dispositif — L'appareil de Clément-Desormes est constitué d'une bonbonne en verre de 25 L dans un habillage en polystyrène expansé. L'air qui s'y trouve peut être considéré thermiquement isolé sur une échelle de temps de quelques secondes. En revanche, la conductivité thermique du verre permet des transferts thermiques sur des durées caractéristiques de l'ordre de la minute. Le goulot de la bonbonne présente trois sorties :

• une soupape qui permet de mettre l'air du ballon en communication avec l'extérieur ;
• un manomètre à liquide permettant de mesurer la pression de l'air de la bonbonne ;
• un robinet pour mettre en communication le récipient avec une poire en caoutchouc. La compression de la poire mettra l'air de la bonbonne sous pression.

Principe de la mesure

Le protocole expérimental présente trois étapes :

1. Après avoir mis en contact la poire et la bonbonne, on imprime à la poire quelques pressions, puis on ferme le robinet. On attend quelques minutes pour que l'air intérieur soit à la même température que l'extérieur. On note \(h_1\) la hauteur de liquide du manomètre.
2. On appuie sur le levier de la soupape pour rétablir l'équilibre mécanique. Le niveau du liquide chute rapidement à 0, moment où on relâchera la soupape.
3. L'air qui reste dans la bonbonne s'est refroidi à cause de la détente rapide qu'il a subie. En attendant quelques minutes que l'équilibre thermique se rétablisse, on voit augmenter la pression. On note alors \(h_2\) la hauteur finale.

À partir des hauteurs \(h_1\) et \(h_2\) on peut en déduire le coefficient calorimétrique \(\gamma\) de l'air moyennant deux hypothèses : d'une part l'air est bien décrit par le modèle du gaz parfait, d'autre part la détente rapide de la phase 2 sera considérée adiabatique réversible. Représentons les trois états décrits plus haut :

Lors de la détente adiabatique on appliquera la loi de Laplace (\(p^{1-\gamma}T^\gamma =\mathrm{C^{te}}\)), et durant la la thermalisation isochore, on appliquera la loi de Charles (\(p/T=\mathrm{C^{te}}\)). On a donc \[ T_0^\gamma(p_0+\delta p_1)^{1-\gamma} =(T_0+\delta T_1)^\gamma{p_0}^{1-\gamma} \quad\text{et}\quad \frac{p_0}{T_0+\delta T_1}=\frac{p_0+\delta p_2}{T_0} \] On en tire \(T_0+\delta T_1=T_0(1+\delta p_2/p_0)^{-1}\). En substituant dans la première relation on obtient \begin{equation} \left(1+\frac{\delta p_2}{p_0}\right)^{-\gamma}=\left(1+\frac{\delta p_1}{p_0}\right)^{1-\gamma} \label{clement-desormes_eq1} \end{equation} Les variations de pression étant très faibles devant \(p_0\) on aboutit au résultat \begin{equation} \gamma = \frac{\delta p_1}{\delta p_1-\delta p_2} \label{clement-desormes_eq2} \end{equation}

Les variations de pression sont mesurées à l'aide de la dénivellation du liquide dans la manomètre. Etant donné que la surpression est proportionnelle à la hauteur \(h\), on en déduit la relation. \begin{equation} \boxed{\gamma = \frac{h_1}{h_1-h_2}}\quad \heartsuit \end{equation}

Manipulation

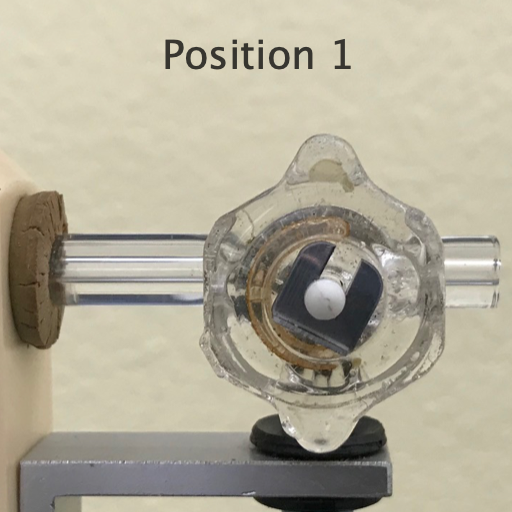
Tout d'abord, retirer la goupille maintenant la soupape ouverte. La bonbonne est dorénavant fermée. Tourner le robinet pour mettre en communication la bonbonne et la poire ➤ position 1. Comprimer l'air par quelques pressions puis isoler le récipient en tournant le robinet de 30° vers la droite ➤ position 2.

 

Attendre 2 minutes 30 l'équilibre thermique puis noter la hauteur \(h_1\).

Appuyer sur le levier de la soupape pour rétablir l'équilibre mécanique. Relâcher lorsque \(h\simeq 0\) (l'ouverture doit durer environ 1 seconde). La pression remonte car le gaz, refroidi par la détente, se réchauffe. Notez la hauteur \(h_2\) après avoir attendu environ 2 minutes 30.

Répéter 6 fois cette expérience en choisissant des valeurs de \(h_1\) assez différentes (comprises entre 20 et 80 mm). Rentrer ces mesures dans un tableau Regressi™ sans oublier d'indiquer les incertitudes-types.

Porter \(h_1\) en fonction de \(\Delta h=h_1-h_2\), puis ajuster une modélisation (que l'on justifiera) à vos données. En déduire la valeur du \(\gamma\) de l'air à température ambiante, avec un niveau de confiance de 95%.

Le moteur de Stirling

Description

Inventé en 1816 par le pasteur et ingénieur Robert Stirling, ce moteur permet de transformer de l'énergie thermique en énergie mécanique à l'instar du moteur à explosion. Mais contrairement à ce dernier, le moteur Stirling utilise un fluide (ici : l’air) contenu dans une enceinte fermée, chauffé par une source de chaleur extérieure à l’enceinte. C’est donc un moteur à combustion externe, avec de nombreux avantages : combustion en continu, plus complète, pas de soupapes d’admission et d’échappement, donc moins de bruit, et possibilité (théorique) d’utiliser tout combustible solide, liquide, gazeux, solaire, nucléaire!

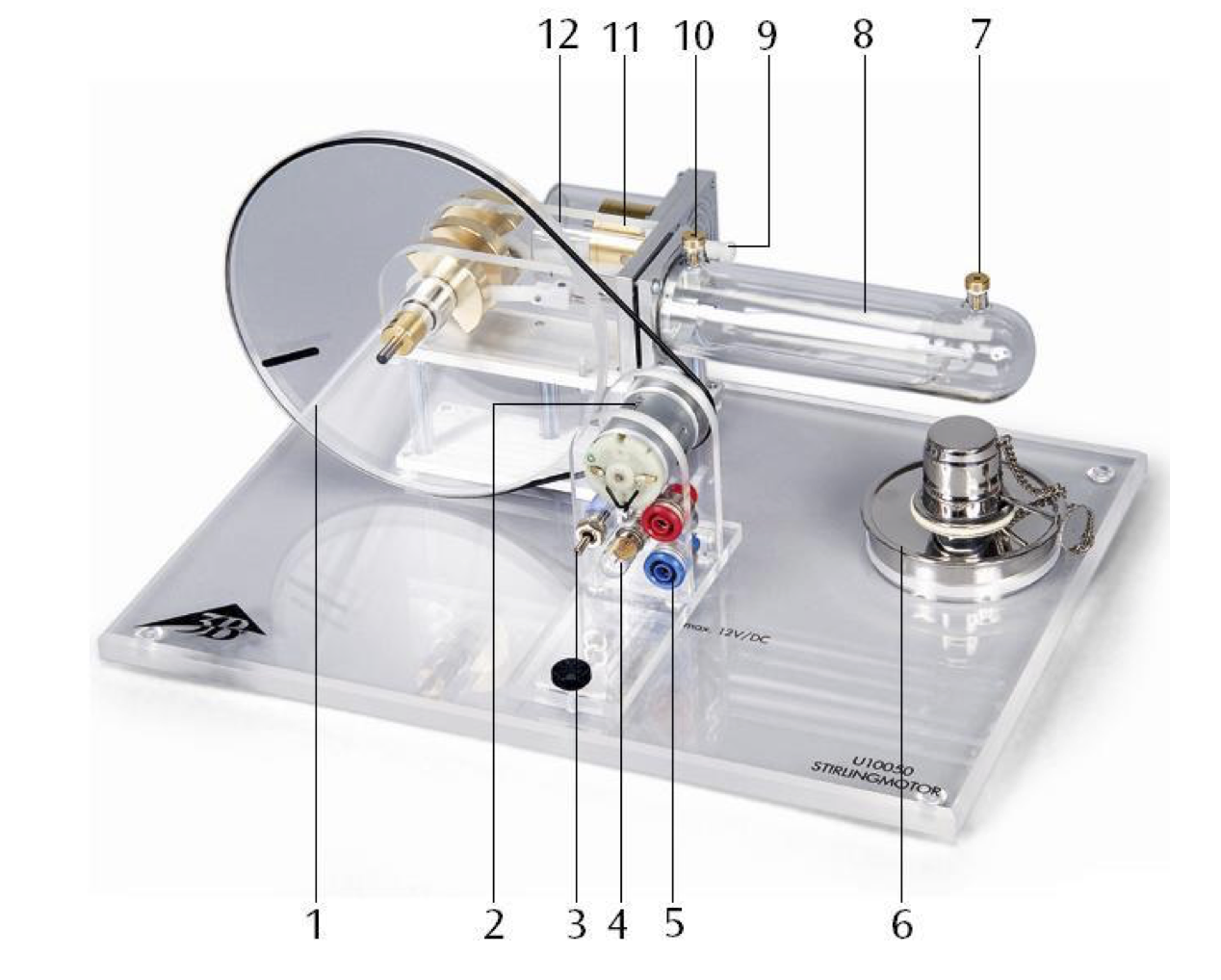
La maquette utilisée ici est constituée d'un bac pour recevoir un brûleur à alcool (6), lequel fera office de source thermique. Un fluide (de l'air ici) est enfermé dans une enceinte hermétique et subit différentes transformations thermodynamiques grâce à l'emploi de deux pistons (8 et 11) qui exécutent des mouvements déphasés de \(\pi/2\). Le piston de travail (11) met en mouvement un volant d'inertie (1) lequel est relié, via une courroie, à un générateur électrique permettant de convertir l'énergie mécanique en énergie électrique.

Cycle thermodynamique

Idéalement, le cycle de Stirling comprend 4 phases :

1. Détente isotherme : le piston de travail recule alors que le piston de refoulement est fixe. L'air chaud voit sa pression diminuer de façon isotherme du fait de l'augmentation de volume. C'est durant cette phase que le moteur produit du travail.
2. Refroidissement isochore : Le piston de refoulement remonte et déplace l'air chaud vers la chambre d'air frais. Ce refroidissement s'accompagne d'une baisse de pression, le volume total restant constant.
3. Compression isotherme : le piston de travail avance, le piston de refoulement étant en position haute. L'air est comprimé de façon isotherme.
4. Chauffage isochore : le piston de refoulement descend ce qui transfère de l'air frais dans la chambre chaude. La pression augmente sans que le volume total ne change.

Ce cycle se traduit par un chemin fermé dans un repère \((V,p)\). Il est décrit dans le sens horaire et son aire représente le travail mécanique fourni par le moteur à chaque tour. En réalité, le cycle s'éloigne sensiblement du cycle réel du fait :

• que les pistons ont un mouvement sinusoïdal plutôt que discontinu ;
• que la compression et la détente ne sont pas tout a fait isothermes ;
• de la présence de frottements et de gradients thermiques dans l'enceinte.

Manipulation

L'objectif de cette expérience est d'obtenir le diagramme de Watt (diagramme pV), pour en déduire la puissance mécanique générée par ce moteur à air chaud.

La pression de l'air est enregistrée à l'aide d'un capteur de pression raccordée à la chambre froide du moteur de Stirling. Le déplacement du piston de travail est enregistré à l'aide d'un capteur potentiométrique ce qui permet de mesurer les variations de volume. Ces capteurs sont connectés à une carte d'acquisition pilotée par le logiciel CASSY Lab™.

Commencer par prendre connaissance du moteur de Stirling et vérifier que les capteurs sont convenablement fixés.

RÉGLAGE DES PARAMÈTRES D'ACQUISITION

Lancer le logiciel CASSY Lab™. Dans l'onglet GENERAL, activer la communication entre le port COM1 de l'ordinateur et la carte d'acquisition CASSY. Dans l’onglet CASSY cliquer sur le capteur de l'entrée A1. Remplir les paramètres suivants : \[ \text{grandeur : déplacement }s_\mathrm{A_1} \quad \text{gamme : }0-15\,\mathrm{cm} \] Cliquer sur le capteur de l'entrée B1 et sélectionner le capteur de pression relative dans la gamme $\pm600\,\mathrm{hPa}$.

Créer la variable $V$ (en cm³) en sélectionnant l'onglet Paramètre/Formule/FFT. Le volume est lié au déplacement $x$ du piston moteur et à son diamètre \(\phi\) par la relation \[ V=x\frac{\pi \phi^2}{4}+\mathrm{C^{te}} \quad\text{avec}\quad \phi=2,5\,\mathrm{cm} \] Comme seules les variations de volume nous intéressent, on prendra \(\mathrm{C^{te}}=0\).

Vérifier en tournant la roue du moteur de Stirling que les capteurs fonctionnent correctement. Notamment, s'assurer que le volume augmente quand on recule le piston moteur.

EXPÉRIENCE (30 MIN)

Remplir la lampe à alcool puis peser-la. Allumer la mèche et déclencher le chronomètre. Placer la lampe au niveau de la chambre chaude puis attendre au moins 2 minutes avant de lancer le moteur (en donnant une rotation initiale à la roue).

Si le moteur s'emballe trop, tendez légèrement le fil relié au piston de travail.

Dans CASSY Lab™, cliquer sur Afficher les paramètres de mesure et fixer un pas d'échantillonnage de 5 ms et un nombre de mesures de 125. Effectuer un enregistrement en cliquant sur , puis tracer le cycle dans un diagramme pV.

On laissera le moteur fonctionner pendant 30 min. Pendant ce temps, on traitera les données.

• Calculer l'aire du cycle (clic droit ⇨ intégrale ⇨ surface de crête) pour en déduire le travail \(W\) fournit par le moteur à chaque cycle.
• Porter le volume en fonction du temps pour ensuite déterminer la période \(T\) du cycle.
• En déduire la puissance mécanique fournie \(P_\text{méca}=W/T\).

Au bout de 30 min, éteindre la lampe à alcool et peser cette dernière. En déduire la masse \(\Delta m\) d'alcool consommée. Sachant que le pouvoir calorifique de l'alcool à brûler vaut 25 kJ/g, en déduire la puissance thermique \(P_\text{th}\) fournie par la lampe à alcool.

Le rendement du moteur, s'écrit, en supposant que toute la chaleur produite par la lampe a été absorbée par le moteur de Stirling, \(\eta=\mathcal{P}_\text{meca}/\mathcal{P}_\text{th}\). Calculer \(\eta\) et conclure.