TP Moments de force

Ce TP aborde l'étude des équilibres mécaniques et est l'occasion de se familiariser avec le concept de moment de force.

Pour les prérequis, voir par exemple femto-physique.fr/mecanique.

Notions théoriques

Moment d'une force

Rappelons qu'une force est caractérisée par :

son point d’application ;
sa direction (ou droite d’action) ;
son sens ;
son intensité que l'on exprime en Newton (N) dans le Système International.

Exemple du poids : Le point d’application du poids est le centre de gravité du corps pesant. La relation qui lie le poids et la masse du corps est la suivante : \[\overrightarrow{P}=m\,\overrightarrow{g}\] avec $\overrightarrow{g}$ le champ de pesanteur dont la norme vaut $g=9,81\mathrm{m.s^{-2}}$.

Considérons maintenant une force $\overrightarrow{f}$ dans un plan $\mathcal{P}$ et un axe orienté $(\Delta)$ perpendiculaire à $\mathcal{P}$. Par définition, le bras de levier est la distance $d$ entre la droite d'action de la force et l'axe $(\Delta)$.

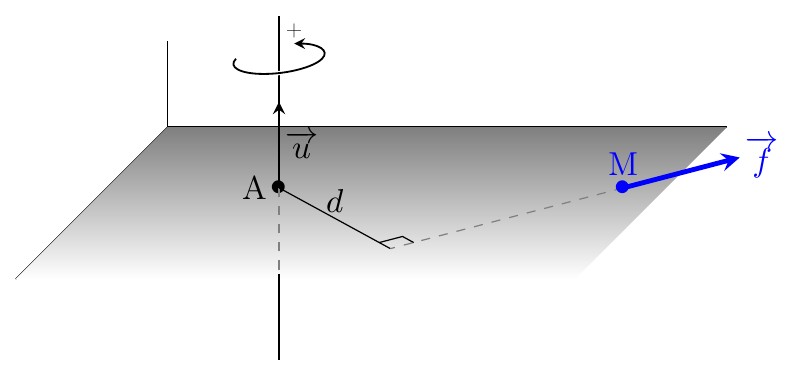
On appelle moment de la force $\boldsymbol{\overrightarrow{f}}$ par rapport à l'axe $(\Delta)$ la quantité \[\mathcal{M}_{\Delta}(\overrightarrow{f})=\pm\, f\times d\] On prendra le signe + lorsque la force tend à faire tourner le point M autour de l'axe dans le sens positif (associé au sens de $\overrightarrow{u}$ par la règle du tire-bouchon) et - dans le cas contraire.

Équilibre d'un solide

Considérons un solide $\mathcal{S}$ en équilibre dans un référentiel $\mathcal{R}$ galiléen. Les lois de la mécanique newtonienne impliquent alors que \begin{equation} \left\{\begin{array}{rcl} \sum\overrightarrow{f}{}^{\textrm{ext}} &=& \overrightarrow{0} \\ \sum\mathcal{M}_{\Delta}{}^{\textrm{ext}} &=& 0 \\ \end{array}\right. \label{tp_moments_eq1} \end{equation} où $(\Delta)$ est un axe fixe quelconque.

Exemple - La poulie différentielle

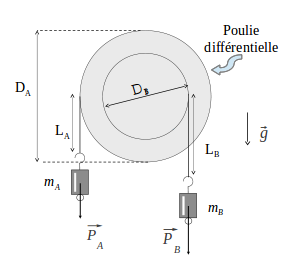
Considérons une poulie différentielle présentant deux gorges de diamètres $D_A$ et $D_B$. Enroulons autour un fil aux extrémités desquelles on fixe deux masses $m_A$ et $m_B$. Choisissons maintenant deux masses de façon à ce qu'elles soient en équilibre comme l'indique la figure ci-contre.

Appliquons \eqref{tp_moments_eq1} sur le système constitué par la poulie. Ce système est soumis à quatre forces :

son poids $\overrightarrow{P}$ passant par son centre
la réaction $\overrightarrow{R}$ du support passant également en son centre
la tension du fil de gauche $\overrightarrow{T}_A$
la tension du fil de droite $\overrightarrow{T}_B$

Calculons le moment de ces 4 forces par rapport à l'axe de rotation $\Delta$ de la poulie. Les forces $\overrightarrow{P}$ et $\overrightarrow{R}$ ont un bras de levier nul et donc un moment nul. Les tensions ont pour moment: \[ \mathcal{M}_{\Delta}(\overrightarrow{T}_A)=+T_A\frac{D_A}{2} \quad\text{et}\quad \mathcal{M}_{\Delta}(\overrightarrow{T}_B)=-T_B\frac{D_B}{2} \] L'équilibre se traduit donc par $T_AD_A=T_BD_B$. Or comme les masses sont en équilibre, on a également $T_A=m_Ag$ et $T_B=m_Bg$. Finalement on trouve la relation \begin{equation} m_AD_A=m_BD_B \label{tp_moments_eq2} \end{equation}

Manipulations

Expérience 1 - La poulie différentielle

La poulie différentielle (métallique, de couleur rouge) est disposée sur un support métallique.

$\spadesuit$ Mesurer les diamètres $D_A$ et $D_B$ des gorges.
Grâce à la théorie (calcul de $X=m_AD_A$ et $Y=m_BD_B$ ainsi que leur incertitude), trouver des masses compatibles avec l'équilibre de la poulie. Puis en les accrochant de part et d’autre de celle-ci, vérifier l’équilibre de l’ensemble comme l'indique la figure de l'exemple précédent (noter quelle gorge intérieure de la poulie a été utilisée).
$\spadesuit$ Changer une des longueurs $L_A$ ou $L_B$, l’équilibre est-il modifié ? Expliquer.
$\spadesuit$ La relation \eqref{tp_moments_eq2} est-elle vérifiée expérimentalement ? Discutez.

Expérience 2 - Vérification de la loi des moments

Tension d'un fil

On utilise un dynamomètre afin de mesurer la force de tension qu'exerce un fil tendu. Pour cela, réaliser le montage de la photo ci-dessus en choisissant une masse importante.

$\spadesuit$ Mesurer la force $F$ exercée par le fil sur le dynamomètre (ne pas oublier de faire le réglage du zéro du dynamomètre). Estimer l'incertitude de votre mesure.
$\spadesuit$ Comparer $F$ au poids $P$ de la masse $m$. Conclusion ? quel est l'intérêt d'utiliser une seule poulie ?

Théorème des moments

On utilise un objet plan qui peut tourner librement par rapport à un axe qui passe par son centre d'inertie. Placer cet objet sur le panneau métallique blanc. Mette également en place 2 poulies aimantées sur ce même panneau.

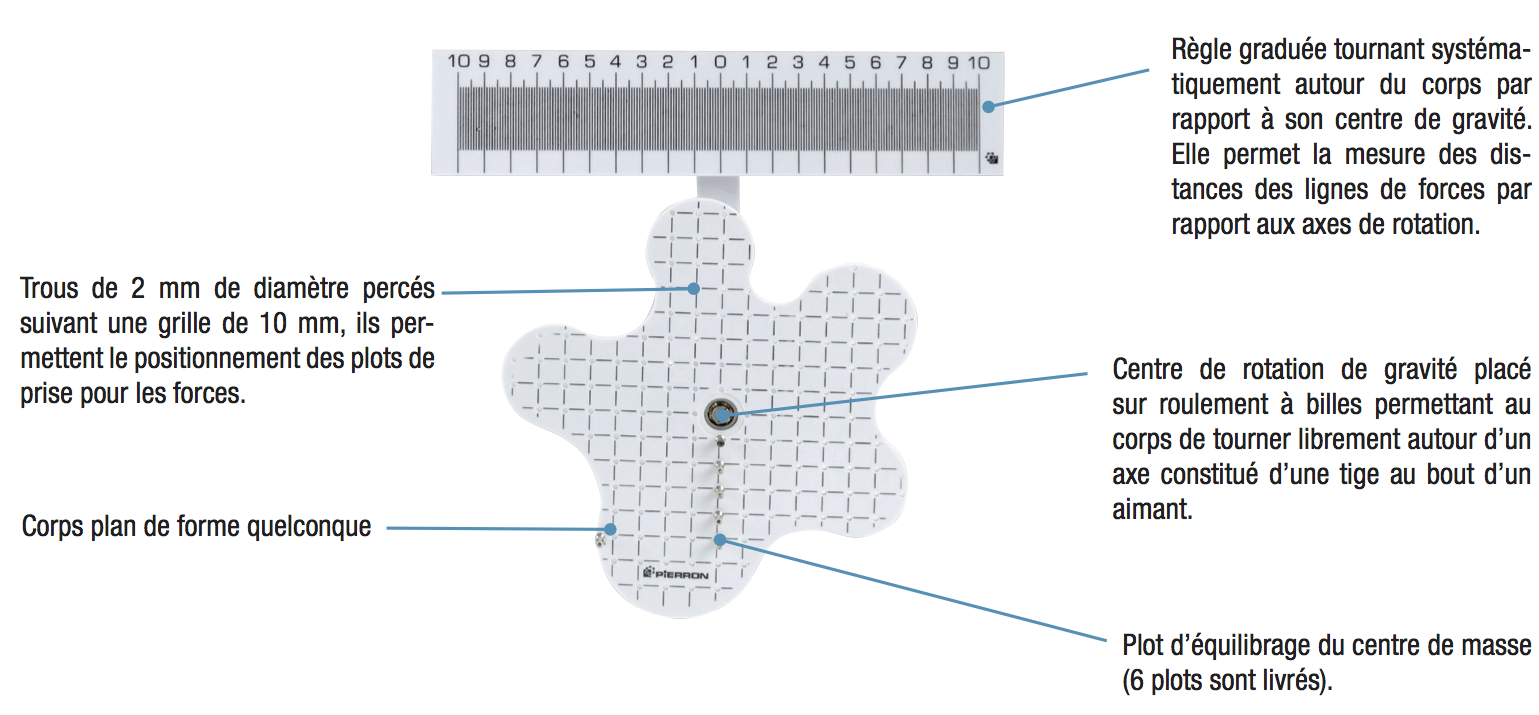
Réaliser le montage ci-dessous. Chaque force de tension présente un bras de levier $d$ par rapport à l'axe de rotation passant par O. Cette distance se mesure en utilisant la règle graduée qui peut pivoter autour de l'axe de rotation.

Attention, vérifier au préalable que la règle est bien perpendiculaire au bras qui la maintient.

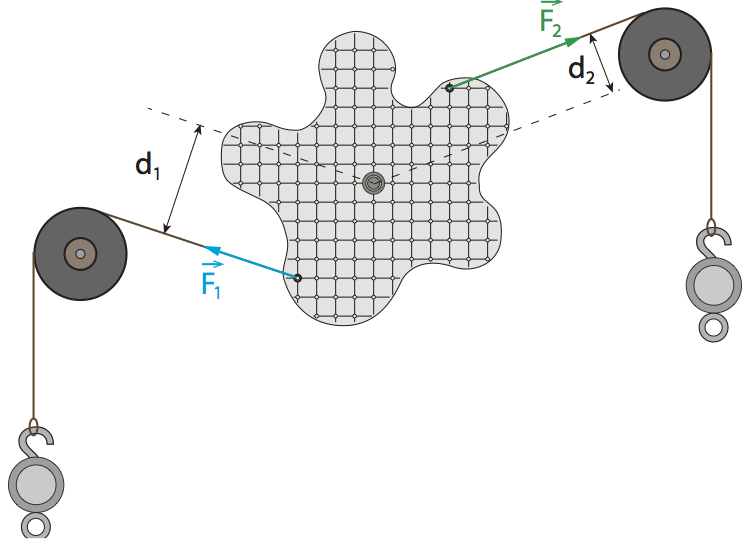
À préparer : Déterminer la relation entre $F_1$, $F_2$, $d_1$ et $d_2$.

Remarque : pour les deux manipulations à venir, ne pas prendre des masses trop différentes (voir annexe). Par ailleurs, On gagne en précision en choisissant de grands bras de levier.

$\spadesuit$ Notez les masses choisies puis mesurer $d_1$ et $d_2$ (ne pas oublier d'estimer les incertitudes).
$\spadesuit$ Dans REGRESSI, entrer les masses $m_1$ et $m_2$, ainsi que les distances $d_1$ et $d_2$. Recommencer pour différents couples de masse (au moins trois mesures différentes) et différents points de fixation.
$\spadesuit$ Calculer les forces $F_1$ et $F_2$ en considérant que $F = P = mg$.
$\spadesuit$ Porter $F_1d_1$ en fonction de $F_2d_2$ (n'oubliez pas les ellipses d'incertitude). Le théorème des moments est-il vérifié ?
$\spadesuit$ Imprimer la courbe et le tableau.

Expérience à faire s'il vous reste au moins 45 minutes

Ajouter une troisième poulie (et une troisième masse) au système afin que l’objet plan soit soumis à trois forces.
$\spadesuit$ Calculer les trois moments par rapport à l'axe de rotation et vérifier la loi des moments.

Forces concourantes

Enlever l’objet plan du panneau métallique puis placer des masses comme sur la figure ci-dessus.

À préparer

Sur un schéma, représenter les forces s'exerçant sur $m_1$, $m$ et $m_2$.
À partir de l’équilibre de la masse $m$, établir deux relations entre $m_1$, $m$, $m_2$ et les angles $\alpha$ et $\beta$.

$\spadesuit$ Choisir $m=$ 200 g. Équilibrer $m$ à l'aide de deux masses puis mesurer α et β à l'aide d'un rapporteur.
$\spadesuit$ Répéter l'opération en changeant les masses $m_1$ et $m_2$ : Le plus simple est de partir du premier équilibre trouvé puis de passer une masse d'un côté à l'autre, d'en rajouter une petite à droit ou à gauche, etc. Notez dans un tableau REGRESSI les valeurs $m_1$, $m_2$, α et β.
$\spadesuit$ Porter $Y=m_2\cos\beta$ en fonction de $X=m_1\cos\alpha$ puis proposer un modèle de régression. Conclure.

★★★

Annexe pour la vérification de la loi des moments (paragraphe 2.2)

A titre indicatif, voici les masses que l’on peut prendre pour effectuer les manipulations dans le cas de deux forces ou trois forces qui s’exercent sur un objet plan.

Manipulation avec deux forces

masse $m_A (kg)$	entre 0.20 et 0.18	entre 0.12 et 0.10	entre 0.10 et 0.08	entre 0.08 et 0.05
masse $m_B (kg)$	entre 0.18 et 0.12	entre 0.16 et 0.12	entre 0.07 et 0.04	entre 0.04 et 0.02

Manipulation avec trois forces

masse $m_A (kg)$	entre 0.20 et 0.18	entre 0.12 et 0.10	entre 0.10 et 0.08	entre 0.08 et 0.05
masse $m_B (kg)$	entre 0.18 et 0.14	entre 0.14 et 0.12	entre 0.08 et 0.06	entre 0.05 et 0.03
masse $m_C (kg)$	entre 0.14 et 0.12	entre 0.16 et 0.14	entre 0.06 et 0.04	entre 0.03 et 0.02

Que mettre dans le fichier de résultats à poster ?

Pour rappel, vous devez déposer votre fichier ici à l'issue du TP

On commentera et discutera tous les résultats/courbes de cette feuille de résultats
On consignera les résultats suivants :
- Le tableau et la courbe $F_1d_1$ en fonction de $F_2d_2$ avec les incertitudes pour la vérification de la loi des moments ; si vous avez eu le temps, celles avec les trois poulies ;
- La courbe $Y$ en fonction de $X$ pour la manipulation des forces concourantes avec la régression (modélisation) associée et les incertitudes.

Matériel

Une poulie différentielle sur support.
Panneau métallique avec poulies et objet plan aimantés.
Un dynamomètre.
Différentes masses et différents fils
Un rapporteur et une règle

masse \(m_A (kg)\)	entre 0.20 et 0.18	entre 0.12 et 0.10	entre 0.10 et 0.08	entre 0.08 et 0.05
masse \(m_B (kg)\)	entre 0.18 et 0.12	entre 0.16 et 0.12	entre 0.07 et 0.04	entre 0.04 et 0.02