Properties of polarized light - polarimetry

Supervisors : J.Geandrot, O.Frantz

This practical work aims to study some phenomena caused by the transversality of light :
dichroism, birefingence, rotating power.

Be careful, the first manipulations are fun but do not waste your time because the last section (6.2 Polarimetry) is quite long.

Two useful videos to understand how to use the Laurent polarimeter:

• Utilisation du polarimètre, réglage du zéro et mesure
• Lecture d'un vernier

Production of polarized light

An electromagnetic wave is the propagation of the field $[\overrightarrow{E},\overrightarrow{B}]$ in vaccuum or in a material medium. The study of the only electric field is enough to deduce the properties of the magnetic field. The wave is transverse (the electric field is perpendicular to the direction of wave propagation) and the direction of the electric field is called polarization of the wave, by convention.

The electrical field can be studied using a sine wave model :

\begin{equation}\overrightarrow{E}= \left(\begin{array}[c]{l} %\begin{systsimple} E_x = E_{x0}\,\cos(2\pi\,\nu\,(t-z/c)+\varphi_{x0}) \\ E_y = E_{y0}\,\cos(2\pi\,\nu\,(t-z/c)+\varphi_{y0}) \\ E_z = 0 \end{array}\right)\end{equation}

This wave is propagating along $(Oz)$. $\varphi_{x0}$ and $\varphi_{y0}$ are the phase offsets of the waves.

Visible light, X-rays, gamma rays, infrared, ultraviolet light and radio waves are electromagnetic waves. A progressive sine wave whose frequency is $\nu$ has a temporal period $T=1/\nu$ and a spatial period (wavelength) $\lambda=c/\nu$.

A wave is plane polarized (linearly polarized) when $\overrightarrow{E}$ keeps a constant direction.

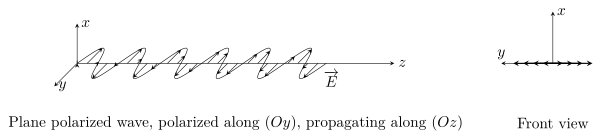
A frequently used coordinate system relates to the plane made by the propagation direction and a vector which is perpendicular to the plane of a reflecting surface : plane of incidence. The component of the electric field parallel to this plane is termed $p$-like (parallel) and the component perpendicular to this plane is termed $s$-like (from senkrecht, German for perpendicular). Polarized light with its electric field along the plane of incidence is thus denoted $p$-polarized, while light whose electric field is normal to the plane of incidence is called $s$-polarized.

A wave is circularly polarized when its two components have a quadrature phase shift ($\Delta\varphi=\pm90^\circ$) and when their magnitudes are equal. Otherwise, it is elliptically polarized : the electric field described an ellipse over time.

Most common sources of visible light, including thermal radiation and fluorescence (but not lasers), produce light described as "incoherent". Radiation is produced independently by a large number of atoms or molecules whose emissions are uncorrelated and generally of random polarizations. In this case the light is said to be unpolarized. One can polarize light, at least partially, using natural phenomena (for example, scattering by the sky or reflection on glass).

Polarization using dichroism

A dichroic material is either one which causes visible light to be split into distinct beams of different wavelengths (colours), or one in which light rays having different polarizations are absorbed differently.

A polarizer (or polariser) is an optical filter that passes light of a specific polarization and blocks waves of other polarizations. It can convert a beam of light of undefined or mixed polarization into a beam with well-defined polarization, i.e. polarized light. A Polaroid polarizing filter is made from polyvinyl alcohol (PVA) plastic with an iodine doping. Stretching the sheet during manufacture causes the PVA chains to align in one particular direction. Valence electrons from the iodine dopant are able to move linearly along the polymer chains, but not transverse to them. So incident light which is polarized in parallel to the chains is absorbed by the sheet; light polarized perpendicularly to the chains is transmitted.

When a second polarizer is placed after the first one, with perpendicular passing directions, no light is transmitted : the polarizers are crossed. The second polarizer is generally called an analyzer.

This property can be used to determine whether light is polarized or not : if, at a certain angle, no light is transmitted through a polarizer then the light is linearly polarized, perpendicularly to this angle.

Polarization by reflection at Brewster’s angle

When light encounters a boundary between two media with different refractive indices, some of it is usually reflected. When unpolarized light is incident from medium 1 on a medium 2 at Brewster’s angle $i_B$, defined by the relation $\tan{i_B}=n_2/n_1$, the light that is reflected is perfectly $s$-polarized.

The physical mechanism for this can be qualitatively understood from the way electric dipoles in the media respond to light. One can imagine that light incident on the surface is absorbed and then reradiated by oscillating electric dipoles at the interface between the two media. The polarization of freely propagating light is always perpendicular to the direction in which the light is travelling. The dipoles that produce the transmitted (refracted) light oscillate in the polarization direction of that light. These same oscillating dipoles also generate the reflected light. However, dipoles do not radiate any energy in the direction of the dipole moment. If the refracted light is $p$-polarized and propagates exactly perpendicularly to the direction in which the light is predicted to be specularly reflected, the dipoles point along the specular reflection direction and therefore no light can be reflected.

Circular polarization

Circular polarizers, also referred to as circular polarizing filters, can be used to create circularly polarized light or alternatively to selectively absorb or pass clockwise (right handed) and counter-clockwise (left handed) circularly polarized light. They are used as polarizing filters in photography to reduce oblique reflections from non-metallic surfaces, and are the lenses of the 3D glasses worn to watch some stereoscopic movies (3D), where the polarization of light is used to differentiate which image should be seen by the left and right eye.

There are several ways to create circularly polarized light, the cheapest and most common involves using a linear polarizer followed by a quarter-wave plate. The linearly polarized light leaving the linear polarizer is transformed into circularly polarized light by the quarter-wave plate. The transmission axis of the linear polarizer needs to be half way (45) between the fast and slow axes of the quarter-wave plate.

3D-glasses consist of two circular polarizers, which are of opposite handedness, mounted in reverse so that circularly polarized light becomes linearly polarized before being filtrated.

A typical waveplate is simply a birefringent crystal with a carefully chosen orientation and thickness. The light travels at different speeds depending on the direction of its electric field. There are two neutral axes, one fast, one slow. The polarization of a linearly polarized wave along a neutral axis is left unchanged. A quarter-wave plate creates a delay of $\lambda/4$ between the fast and the slow components, i.e. $\Delta\varphi=90$.

\begin{equation}\begin{array}[c]{c} { \left(\begin{array}[c]{l} E_x = E_{x0}\,\cos(2\pi\,\nu\,(t-z/c)) \\ E_y = E_{y0}\,\cos(2\pi\,\nu\,(t-z/c)) \\ E_z = 0 \end{array}\right) } \\ %fr \text{polarisation rectiligne} \text{linear polarization} \end{array} \leadsto \begin{array}[c]{c} { \left(\begin{array}[c]{c} E_x = E_{x0}\,\cos(2\pi\,\nu\,(t-z/c)) \\ E_y = E_{y0}\,\sin(2\pi\,\nu\,(t-z/c)) \\ E_z = 0 \end{array}\right) } \\ %fr \text{polarisation circulaire} \text{circular polarization} \end{array}\end{equation}

Change in polarization by delaying the $E_y$ component of 90.

Polarization by birefringence

Birefringence is the optical property of a material having a refractive index that depends on the polarization and propagation direction of light. Crystals with asymmetric crystal structures are often birefringent, as are plastics under mechanical stress. Birefringence is responsible for the phenomenon of double refraction whereby a ray of light, when incident upon a birefringent material, is split by polarization into two rays taking slightly different paths.

Polarimetry

In 1817, drawing on the work of Arago, Biot studied the effects of certain solutions on the polarization of light. He thus layd down the following laws :

• Some isotropic transparent material, in which a monochromatic, linearly polarized, light beam travels, rotates the plane of polarization around the propagation direction of the beam. This substance is said to be optically active.
• A dextrorotatory medium causes linearly polarized light to rotate to the right.
  A levorotatory medium causes linearly polarized light to rotate to the left.
• The angle $\alpha$ (degrees) of optical rotation is proportional to path length $\ell$ (dm), concentration $C~(\mathrm{g.cm^{-3}})$ and specific rotation $[\alpha]$, which depends on the material, temperature and wavelength.

  \begin{equation}\boxed{\alpha=[\alpha]\,\ell\,C} \quad \heartsuit \end{equation}

  Please be careful to use these units as the specific rotation is usually given with them.

Laurent’s polarimeter

Laurent’s polarimeter precisely measures the polarization direction of a light beam. It is made of a linear polarizer, a half-wave plate in the central part of the beam, a tank (length $\ell$) and a second linear polarizer (analyzer).

A half-wave plate transforms a linearly polarized light into another linearly polarized light, whose polarization direction is symmetrical with respect to its fast axis.

When the analyzer is perfectly balanced with the halfwave plate, the observed disc is uniform and dark.

Without any optically active solution, the polarization direction does not turn. The measured angle is close to zero (calibration stage). With the solution, the polarization direction turns through an $\alpha$ angle. As a consequence, the analyzer has to be turned through the same $\alpha$ angle to get the uniform and dark disc back.

A vernier improves the accuracy of the measured angle. Two sets of markings are engraved on the device : a fixed one and a moveable one (the vernier). The vernier consists of 20 graduations spread over 19 others. As a consequence, each marking is shifted by $1/20=0{,}05$, which defines its accuracy. If the zero of the vernier is shifted by $p/20$ from a main tick, then, by progressive shifting, the $p$-th scale of the vernier coincides perfectly with a graduation of the fixed part. This tick of the vernier is finally added to the main measure, after the decimal point, to increase its accuracy. Note that it is often easier to check out the vernier by taking a picture of it (e.g. with a smartphone).

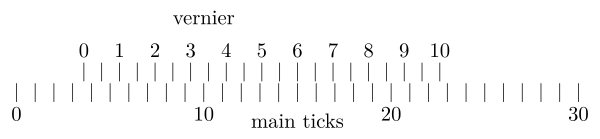
The zero of the vernier is between the 3rd and the 4th of the main graduation.
The first coincidence between graduations takes place at the 6th of the vernier.
The result of the measurement is $3{,}60 \pm 0{,}03$ degrees.
(which is consistent with what is being measured with the naked eye).

Sucrose’s specific rotation

As the angle of rotation is proportional to the concentration of the optically active compound, we will prepare three solutions of sucrose with different concentrations : 160 g/L, 80 g/L and 40 g/L. The first one is made by dissolving sugar into tap water, using a weighing scale and a volumetric flask. Make sure you mix the solution until all sugar is dissolved. Store this first solution as it will be diluted to prepare the others.

Once your solution is ready, pour it into the analysing tube. An air bubble often pops up in the tube. If it is small enough, you can use the bulge to capture it and thus avoid refraction in the path of light. Be careful, the glass lid is fragile and we do not have spare ones.

Afterwards, place the tube in the polarimeter, turn the analyzer until you get the dark, uniform disc. Finally read the angle thanks to the vernier.

Tasks

Preparation

Read the preceding text. Write down the words you do not understand, with their translation and pronunciation. A dictionary can be useful (http ://www.wordreference.com)

Calculate the typical value of Brewster’s angle $i_B$ for an air-glass interface.

How can you find the neutral axis of a quarter-wave plate ? (using two crossed polarizers)
Provide a drawing with a legend.

How do you check that light is linearly polarized ?
How do you check that light is circularly polarized ? (using a quarter-wave plate and an analyzer).
Provide drawings.

What is the value of $\theta$ on the figure on the right ?

Find the typical specific rotation of sucrose on the internet. What does it depend on ?

Manipulations

Polarization using dichroism (1.1.1) (10’)

Look through two polarizers while rotating one of them. What happens ?

Place a linear polarizer in front of each of your eyes. Make sure these two polarizer are crossed. Look at yourself in a mirror. Close an eye. Do you observe something unusual ?

Polarization by reflection at Brewster’s angle (1.1.2) (10’)

Observe light, as reflected by a window, through a polarizer (used as an analyzer).

Is the light polarized ? Try for $i=0$ or $i\simeq i_B$ and conclude.
If polarized, in which plane ($s$ or $p$) ?

Circular polarization (1.1.3) (30’)

Find the neutral axis of the quarter waveplate.

Look at yourself in a mirror, wearing now a pair of 3D-glasses. Close an eye. What do you observe ? Find an explanation (what does a mirror do on circularly polarized light ?).

In the following, we want to check how is made a pair of 3D-glasses.

Confirm the linear polarization of light traveling from outside to inside. What is the polarization direction ?

Verify that light traveling from inside to outside is not linearly polarized. Using a quarter-wave plate and an analyzer, prove that light traveling from inside to outside is circularly polarized.

Polarization by birefringence (1.1.4) (10’)

Look at some text through the given crystal. What happens ?
Explain using birefringence property.

Place a polarizer/analyzer between the eye and the crystal. What do you observe when the passing direction of the analyzer changes ? Conclude on the link between polarization and birefringence of this crystal.

Sucrose’s specific rotation (1.2.2) (60’)

How much sugar should you dissolve in the flask in order to obtain a concentration of 160 g/L ?

Prepare the three solutions and for each one of them find the angle $\alpha$ of optical rotation thanks to the Laurent polarimeter.

Identify the sources of uncertainty on $\alpha$ and $C$. Quantify them.

Plot $\alpha$ vs concentration $C$ (four points). Do not forget to show uncertainties.

Does the Biot’s law apply here ? If it does, give specific rotation of sucrose and tell whether it is dextrorotatory or levorotatory.