TP : étude du prisme à l'aide d'un goniomètre

Responsable : J. Roussel

Aspects théoriques

Considérons un prisme droit de base triangulaire, transparent d'indice de réfraction $n$. On s'intéresse aux rayons lumineux se propageant dans un plan de section principal (perpendiculaire à l'arête du prisme). On note $A$ l'angle du sommet qui fait face à la base du triangle (cf. Figure ci-dessous).

Formules du prisme

Les lois de la réfraction imposent deux relation entre $i$ et $r$ puis entre $i'$ et $r'$ : \[ \left\{\begin{array}{ccc} \sin i &=& n\sin r \\ \sin i'&=&n\sin r' \end{array}\right. \] La déviation $D$ que subit le rayon incident s'écrit : \[D=(i-r)+(i'-r')\] De plus, $A$, $r$ et $r'$ sont liés par \[A+(\frac{\pi}{2}-r)+(\frac{\pi}{2}-r')=\pi\] D'où l'on déduit une nouvelle expression de $D$ : \[D=i+i'-A\] Si $A$ et $n$ sont fixés, $D$ ne dépend que de l'angle d'incidence $i$. Sur la Figure, on a représenté la déviation $D$ en fonction de $i$ en fixant $A=60$° et $n=1,6$.

 

Minimum de déviation

Conditions d'émergence

On remarque sur la figure précédente que la déviation n'existe que si l'angle d'incidence dépasse une valeur $i_{0}$. En effet, si $i$ est trop petit il y a réflexion totale à l'intérieur du prisme. Par exemple, avec un prisme tel que $A=60^{\circ}$ et $n=1,7$, on a \[\sin i'\leq1\Rightarrow\sin r'\leq\frac{1}{n}\Rightarrow r'\leq36{}^{\circ}\] d'où l'on tire \[r\geq24{}^{\circ}\Rightarrow i\geq43,7{}^{\circ}\]

Formule de la déviation minimale

Sur la figure précédente, on note également l'existence d'une déviation minimale notée $D_{\rm m}$. La mesure de cette déviation minimale permet de déduire l'indice de réfraction $n$. En effet, d'après le principe du retour inverse de la lumière, si $D$ est la déviation correspondant à une incidence $i$, alors $D$ est aussi la déviation correspondant à l'incidence $i'$. Il existe donc deux angles d'incidence donnant la même déviation. Ainsi, lorsque $D$ atteint son minimum, ces deux angles doivent se confondre (voir courbe) : \[i=i' \quad\text{quand}\quad D=D_{{\textrm{m}}}\] Dans ce cas, on a $r=r'=A/2$ et $D_{\rm m}=2i-A$. La loi $n=\sin i/\sin r$ donne finalement

\begin{equation} \boxed{\displaystyle n=\frac{\sin{\displaystyle {\left(\frac{A+D_{{\textrm{m}}}}{2}\right)}}}{\sin{\displaystyle {\frac{A}{2}}}} } \label{eq:tp1_formule_du_prisme} \end{equation}

La mesure de $D_{\rm m}$ et $A$ permet donc de calculer l'indice du prisme.

Manipulation

Description du goniomètre

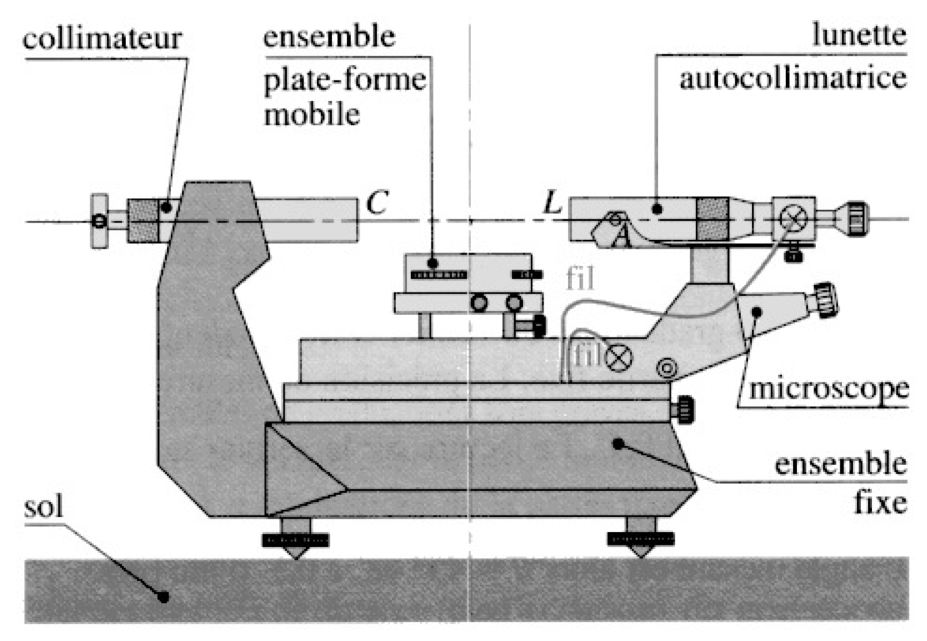
Le goniomètre est un appareil destiné à la mesure précise des angles (précision de l'ordre de la minute d'arc !).

Il est composé de quatre parties :

• Une plate-forme mobile (la platine) autour d'un axe vertical destiné à recevoir le prisme. Trois vis permettent de régler l'horizontalité de la platine.
• Une lunette auto-collimatrice mobile autour d'un axe vertical destinée à observer des objets à l'infini.
• Un collimateur fixe constitué par une fente de largeur réglable, placée dans le plan focal objet d'une lentille convergente.
• Un microscope permettant la lecture des angles à la minute près ($1'= 1/60^{\circ}$).

Réglages

Avant d'effectuer les mesures, il est nécessaire de régler la lunette, le collimateur ainsi que l'horizontalité de la plateforme (effectué par l'enseignant). Commencer par allumer une lampe spectrale.

Réglage de la lunette auto-collimatrice

Dans la lunette, entre oculaire et objectif se trouve un réticule (2 fils croisés et perpendiculaires) que l'on peut éclairer en basculant un miroir semi-transparent. La lunette est bien réglée lorsqu'elle est afocale : elle donne d'un objet à l'infini une image à l'infini comme la lunette astronomique (visible par un œil normal sans accommoder). Pour cela on procède à un réglage par auto-collimation :

1. Éclairez le réticule en basculant le petit bouton situé sur le côté de la lunette ;
2. Réglez le tirage de l'oculaire pour voir nettement sans accommoder le réticule. Ce dernier est alors dans le plan focal de l'oculaire.
3. Appliquez un miroir plan contre l'objectif et réglez le tirage de l'objectif, par rotation du bouton moleté, pour que le réticule image soit dans le même plan que le réticule objet : on voit alors deux réticules aussi net l'un que l'autre. Le réticule se trouve alors dans le plan focal de l'objectif. La lunette est réglée !

Réglage du collimateur

Un collimateur sert à collimater un faisceau c'est-à-dire, à produire un faisceau de rayons parallèles. Le réglage du collimateur consiste à faire en sorte que la fente source se situe dans le plan focal objet de la lentille du collimateur. On procède de la façon suivante :

1. Amenez une lampe spectrale tout près de la fente du collimateur. Pensez à ouvrir la fente d'entrée (pas trop tout de même !).
2. Visez le collimateur avec la lunette en confondant à peu près leurs axes optiques respectifs. Tournez la bague du collimateur de façon à voir une image nette de la fente. l'image de la fente est à l'infini. Le collimateur est réglé !

Mesure de A

Pour mesurer l'angle au sommet du prisme, procédez comme suit :

1. Une fois le prisme sur la plateforme n'y touchez plus. Fixez la plateforme ; elle ne doit pas tourner pendant cette mesure.
2. Effectuez une auto-collimation sur une des faces du prisme, autrement dit, dirigez la lunette —réticule éclairé— en direction d'une face qui par réflexion produira une image du réticule dans le même plan, que le réticule. Faites coïncider le fil vertical du réticule avec son image. Dans ce cas, la face est perpendiculaire à l'axe de la lunette. Repérer l'angle $\alpha_{1}$ sur le vernier (utilisez le réglage fin).
3. Faites la même chose avec la deuxième face transparente du prisme. Mesurez $\alpha_{2}$.
4. Faites un schéma et déduire l'angle $A$ en fonction de $\alpha_1$ et $\alpha_2$.
5. Calculez $A$ ainsi que son incertitude.

Mesure de $\boldsymbol{D_{\rm m}}$

Pour mesurer la déviation minimale, effectuez les opérations suivantes.

1. Éteignez le réticule et ouvrez la fente du collimateur. Tournez le plateau de façon à ce que le faisceau entrant ne subisse pas de réflexion totale à l'intérieur du prisme. Cherchez à l'œil nu le faisceau émergeant. Vous devez observez un spectre discontinu.
2. Visualisez le spectre de la source à l'aide de la lunette et choisissez une raie spectrale. Ajuster la largeur de la fente de façon à obtenir une précision maximale.

   Lampe spectrale	longueur d'onde (nm)	couleur
   Mercure	578,0	doublet jaune
   	546,0	vert
   	435,8	bleu-indigo
   	404,6	violet
   Cadmium	643,8	rouge
   	508,5	vert
   	480,0	bleu
   	467,8	bleu

   En tournant le plateau (et donc en modifiant l'angle d'incidence), remarquez que le faisceau émergeant tourne d'un côté puis rebrousse chemin ; à ce moment précis, la déviation est minimum. Lisez l'angle $\alpha$ correspondant à ce minimum. Notez que la précision de la mesure dépend --entre autre-- de la finesse des raies.
3. S'il vous reste moins de 30 minutes : Après avoir collecté les valeurs de $\alpha$ pour trois raies, enlever le prisme et viser le collimateur. Mesurer la valeur $\alpha_0$ correspondant au trajet direct. On a alors $D_m=|\alpha-\alpha_0|$.
4. S'il vous reste plus de 30 minutes : Répétez l'opération 2 après avoir tourné la platine de façon à échanger les rôles des faces d'entré d'entrée et de sortie. Lisez les angles $\alpha'$ correspondant au minimum de déviation. On a alors \[2D_{\rm m}=|\alpha-\alpha'|\]

Faites la mesure de $D_{\rm m}$ pour différentes longueurs d'onde (au moins trois). On fera une estimation de l'incertitude sur $D_{\rm m}$ (type B). Dans Regressi™, remplissez un tableau avec les grandeurs $A$, $\lambda$ et $D_{\rm m}$. Créez la grandeur calculée $n$. Complétez le tableau en ajoutant les incertitudes (Cliquez sur Incertitudes pour faire apparaître les colonnes relatives aux incertitudes.)

Loi de dispersion

Dans le domaine visible, on prévoit que l'indice suit la loi de Cauchy, c'est-à-dire \[ n(\lambda)=C_{1}+\frac{C_{2}}{\lambda^{2}} \qquad\text{avec}\qquad C_2>0 \] On cherche à vérifier cette loi. À l'aide d'une régression, vérifiez la validité cette loi (n'oubliez pas d'afficher les barres d'erreur sur le graphique). Vos mesures sont-ils en accord avec la théorie ? si oui, en déduire les paramètres $C_{1}$ et $C_{2}$.

★★★