| 

Surface tension

Supervisors : O. Frantz, J. Geandrot

Surface tension

It costs energy to increase the surface of a liquid. A liquid thus adopts the form that minimizes its surface. If the only forces that apply to a liquid are those of surface tension, it can be shown that the area that minimizes the energy is a sphere. That is why soap bubbles are spherical.

Surface tension $\gamma$ measures the resistance to the increase in surface: if the surface S of a liquid varies by dS, then the energy of the liquid increases by $\mathrm{d}{E}=\gamma\,\mathrm{d}S$.

If now we consider a liquid film on a rectangular frame with one movable side, the liquid tries to minimize its surface by exerting a force on that side. The force required for the operator to maintain the area constant is $f=2\,\gamma\,\ell$ where $\ell$ is the length of the rod. The force is doubled through factor 2 because there are two interfaces: one above and one below.

A droplet lying on its support

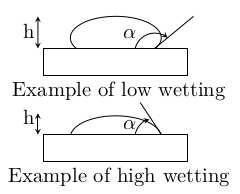
The shape of a droplet of liquid in equilibrium with its environment is due to the surface tension forces (aka capillary actions). The contact angle $\alpha$ is defined in the following figure. When it exceeds 90°, the liquid shows a low wettability.

If the top of the droplet has zero curvature, a simple relationship links its height to the surface tension: \[ h=\sqrt{2\,\gamma\,\dfrac{1-\cos\alpha}{\rho\,g}} \] Therefore the surface tension can be calculated from the shape of the droplet: \begin{equation} \boxed{\gamma=\dfrac{\rho\,g\,h^2}{2(1-\cos\alpha)}} \label{eq:gammaforme} \end{equation} with $\rho$ the density and $g$ the earth gravity field.

Direct measurement: Du Noüy ring method

For the direct measurement of the surface tension, we use a precision dynamometer as shown on the apparatus below, which gives the strength that the surface of the liquid exerts on the ring (until its detachment of this surface) along with the weight of the ring. This force approximately equals \(f=4\pi\,r\,\gamma+m\,g\) at its maximum, since it is exerted on the inner and outer edges of the ring. \begin{equation} \boxed{\gamma=\dfrac{f-m\,g}{4\pi\,r}} \label{eq:gammadirect} \end{equation}

Jurin's law

The rise and fall of a liquid within a thin capillary tube (aka capillary ascent) can be described by Jurin's law, provided that the tube is thin enough. The hydrostatic equilibrium results from the competition between gravity and surface tension. Jurin's law links the height of the ascent to the radius of the tube: \[ \boxed{h=\frac{2\,\gamma\,\cos\theta}{\rho\,g}\,\frac{1}{r}}\] $\gamma$ is the surface tension of the liquid and $\theta$ the contact angle.

Tasks

Preparation

Find the values of the surface tension of water and soapy water (on the internet).

Express uncertainty on surface tension $\gamma$, from formula \eqref{eq:gammaforme}, based on uncertainties on the droplet's height and angle. The density and the acceleration of gravity are precise enough in order to neglect their influence on the total uncertainty.

Manipulations

A droplet lying on its support (45')

Place a drop of water on a clean rubber support (large stopper).

Make the image of the droplet on a screen using a lamp and a lens. Make sure you choose the right lens.

Reproduce the image of the droplet on a sheet of paper and project the image of a ruler to determine the enlargement of the lens.

Measure the height of the droplet and the contact angle (take the average value of the two angles). Assess the uncertainties on the height and angle.

Find the value of the surface tension of this droplet and its uncertainty. The acceleration of gravity is $g=9{,}8~\mathrm{m.s^{-2}}$.

Start again with soapy water.

Du Noüy ring method (30')

Fill the small crystallizer with water.

Measure the weight of the ring with the dynamometer and eventually hide this weight using the sliding over-tube.

Slowly lower the laboratory scissor jack and write down the maximum strength as shown by the dynamometer, before the ring is pulled off the water.

Deduce the surface tension of water at room temperature and the uncertainty of the measure. Do not forget to deduct the weight of the ring.

Start again and add surfactant into the water (a few drops of dish soap).

Remove the ring after the experiment to preserve the spring of the dynamometer.

Jurin's law (45')

Fill the Jurin device with tap water (clean well beforehand). Observe the rise. It may be necessary to tap or slightly shake the tubes to help the water to rise.

Take a photo then measure (using Regressi for example) the height of rise $h$ for the different tubes, then check Jurin's law using a linear regression.

For water, $\cos\theta\simeq 1$. Deduce the value of $\gamma$ and its uncertainty.