TP Oscillateur de torsion

Oscillations d'un pendule de torsion

Description

Le pendule de Pohl est un oscillateur de torsion constitué de quatre éléments.

1. Un disque en rotation autour de son centre. Un pointeur placé sur le disque permet de repérer l'angle de rotation \(\theta\).
2. Un ressort spiral, qui exerce un couple mécanique qui tend à ramener le disque vers sa position d'équilibre.
3. Un système de freinage électromagnétique qui permet d'amortir plus ou moins les oscillations.
4. Un moteur, relié au ressort spiral, qui permet de forcer les oscillations à une fréquence ajustable par l'utilisateur.

Lorsqu'on tourne le disque d'un angle \(\theta\), le ressort spiral s'enroule (ou se déroule) ce qui fait apparaître une force de rappel dont le moment mécanique s'oppose au moment appliqué au disque. Si on lâche le disque, le système retrouve son état d'équilibre en oscillant : c'est le régime d'oscillations libres.

Si l'on soumet le pendule à une force excitatrice sinusoïdale de fréquence \(f_e\) (Hz), le système se met à osciller à la même fréquence : c'est le régime sinusoïdal forcé.

Modèle théorique

La grandeur physique étudiée en fonction du temps est l'angle de torsion \(\theta\) (c’est le degré de liberté du système). On obtient l'équation du mouvement en appliquant le théorème du moment cinétique (cf. cours sur le théorème du moment cinétique) au disque (système d'étude).

Le système est soumis à trois moments mécaniques orientés suivant l'axe de rotation.

• Le moment de rappel \(\mathcal{M}_1\) produit par le ressort spiral. La propriété d'un tel ressort est que ce moment est d'autant plus fort que la torsion du ressort est importante. On a \(\mathcal{M}_1 = -C \theta\) où \(C\) désigne la constante de torsion du ressort (N.m/rad).
• Le moment \(\mathcal{M}_2\) dû au freinage électromagnétique. Ce type de frottement a la particularité d'être proportionnelle à la vitesse du système en général, et donc à la vitesse angulaire ici. On a \(\mathcal{M}_2 = -h\,\dot \theta\) où \(h\) est un coefficient de frottement.
• Le moment extérieur périodique \(\mathcal{M}_\text{ext}(t)\) imposé par le moteur.

Par ailleurs, le disque présente un moment d'inertie \(J\) par rapport à l'axe de rotation. Le théorème du moment cinétique s'écrit donc : \[ \dfrac{\mathrm{d}L}{\mathrm{d}t}= \mathcal{M}_1+\mathcal{M}_2+\mathcal{M}_\text{ext} \quad\text{avec}\quad L=J\dot \theta \] soit l’équation différentielle suivante  \begin{equation} J\,\ddot \theta + h\,\dot \theta + C\,\theta = \mathcal{M}_\text{ext}(t) \label{eq1} \end{equation}

Les différents types d'oscillations libres

Lorsque le moteur est éteint, on a \(\mathcal{M}_\text{ext}(t)=0\) et l'équation différentielle \eqref{eq1} prend la forme suivante  \begin{equation} \boxed{ \ddot\theta + 2\,\lambda\,\dot \theta + {\omega_0}^2\theta = 0 } \quad\text{avec}\quad \left|\begin{array}{l} \text{ \(\lambda\) : le coefficient d'amortissement ;}\\ \text{ \(\omega_0\) : la pulsation propre des oscillations.}\\ \end{array}\right. \end{equation}

Cette équation est caractéristique des oscillateurs harmoniques amorties. On distingue trois types de comportement.

Régime pseudo-périodique

Si le coefficient d'amortissement \(\lambda\) n'est pas trop élevé, on observe des oscillations dont l'amplitude s'amortit exponentiellement au cours du temps. On parle d'oscillations pseudo-périodiques. Plus précisément, \[ \text{si }\lambda<\omega_0\qquad \theta(t) = A e^{-\lambda\,t} \cos (\omega t + \phi) \quad\text{avec}\quad\omega=\sqrt{{\omega_0}^2-\lambda^2} \]

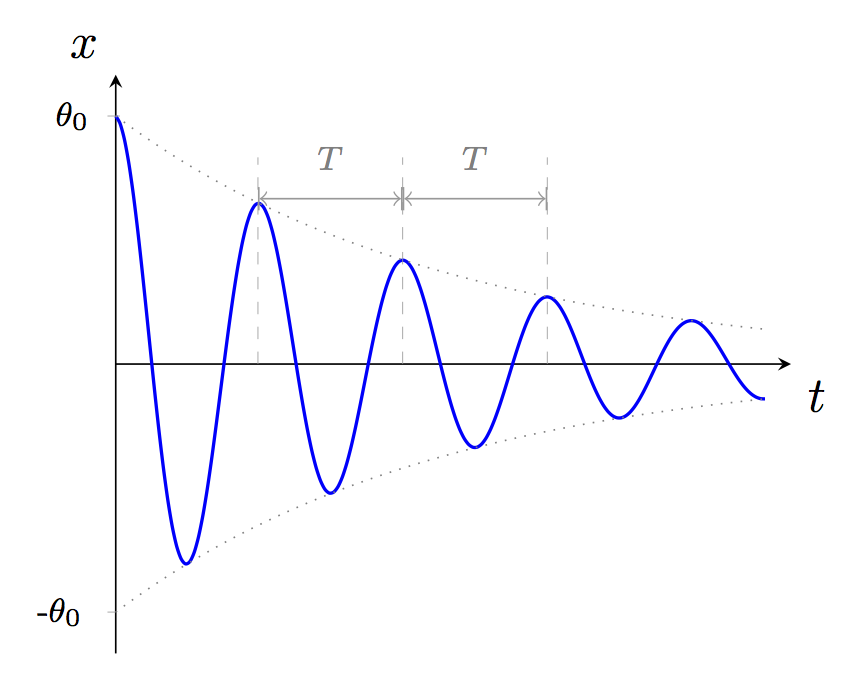
La durée d'une oscillation vaut \[ \boxed{T = \dfrac{2\pi}{\omega} = \dfrac{2\pi}{\sqrt{\omega_0^2 - \lambda^2}}} \] Comme on le voit, la durée d'une oscillation augmente avec le coefficient d'amortissement.

La figure ci-contre illustre le comportement des oscillations avec pour conditions initiales : \(\theta_0 = \theta_{t=0} = \theta_{max}\) ; \(\dot{\theta}_{t=0} = 0\).

Pour mesurer l'amortissement des oscillations, on définit le décrément logarithmique par : \[ \boxed{\Lambda =\ln \left[\frac{\theta(t)}{\theta(t+T)}\right]} \]

Régime critique

Lorsque \(\lambda = \omega_0\), le pendule retourne dans un minimum de temps à sa position d’équilibre, sans osciller ; \(\theta(t)\) ne change pas de signe. Dans ce cas, la solution de l’équation différentielle est \[ \theta = \theta_0\, \mathrm{e}^{-\lambda\,t} (1+\lambda\,t) \]

Cas apériodique

Lorsque \(\lambda > \omega_0\), le pendule retourne asymptotiquement à sa position d’équilibre, ceci d'autant plus lentement que \(\lambda\) est grand.

Oscillations forcées.

Lorsque le moteur est en marche, il impose un moment sinusoïdal de pulsation \(\omega_e\) ajustable. On a \[ \mathcal{M}_\text{ext}(t) = \mathcal{M}_0\,\cos(\omega_e\,t) \] La fréquence correspondante est donnée par \(f_{e}=\omega_e/2\pi\).

L’équation différentielle \eqref{eq1} devient :

\begin{equation} \ddot\theta + 2\,\lambda\,\dot\theta + {\omega_0}^2\theta = A\,\cos(\omega_e\,t) \quad \text{où \(A\) est une constante.} \end{equation}

En régime forcé (lorsque le régime transitoire est négligeable), la solution de cette équation est \[ \theta(t) = \theta_\mathrm{a}\,\cos(\omega_e\,t+\phi) \] avec \(\theta_\text{a}\) l’amplitude des oscillations qui dépend (comme \(\phi\)) de la pulsation \(\omega_e\) imposée.

Manipulations

Dispositif expérimental

Le dispositif expérimental est constitué de 4 éléments.

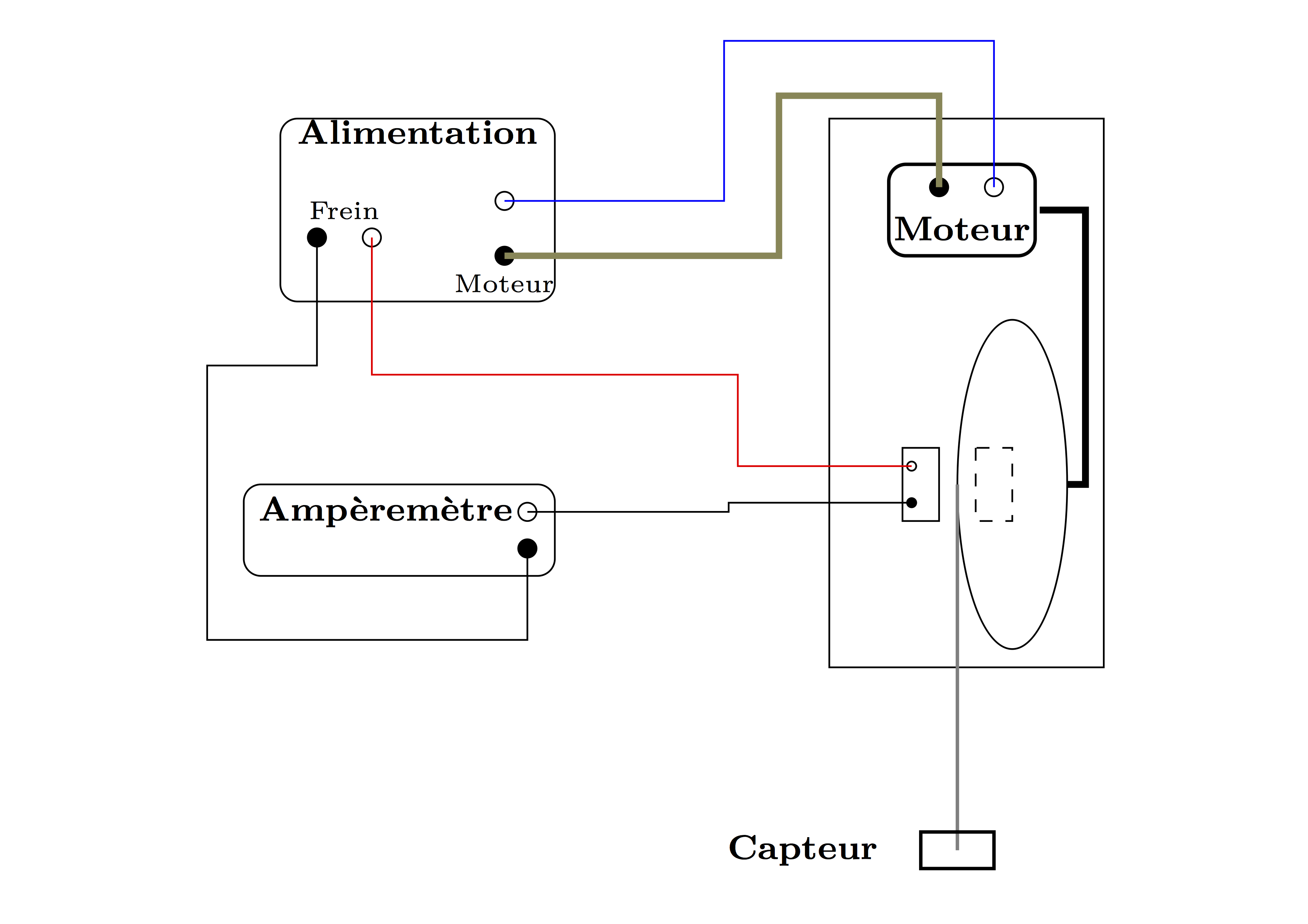
1. Un pendule de Pohl.
2. Un capteur de mouvement relié au disque du pendule par un fil. Le mouvement du fil est traduit en un signal proportionnel à l'angle \(\theta\). Une interface et un logiciel (cassylab™) permet l'exploitation directement sur l'ordinateur dédié.
3. Une alimentation de 24 V alimente le moteur continu qui, à l'aide d'un bras articulé, produit un moment d'excitation périodique. La fréquence d'excitation \(f_e\) est ajustable à l'aide des boutons GROB (réglage grossier) et FEIN (réglage fin) situés sur le moteur.

4. Une source de courant (2 A max) alimente un système de freinage par courants de Foucault. Le coefficient d'amortissement \(\lambda\) est proportionnel à l'intensité \(I_h\) produite par la source de courant. L’unique bouton de réglage de l’alimentation permet de choisir ce courant et un ampèremètre placé en série permet d'avoir sa valeur précise.

Vérifier que le montage est correctement effectué.

Étude du régime pseudo-périodique

Le moteur est ici éteint ; seul le circuit d’alimentation de l’électro-aimant est indispensable.

Commencer par ouvrir le logiciel cassylab™ puis suivre la notice fournie afin d'effectuer les réglages. Vous choisirez des paramètres d'acquisition qui permettent d'avoir des courbes les plus lisses possible.
D'autre part, les paramètres de mesures permettent de régler la précision des données enregistrées : on pourra choisir les paramètres pour avoir le temps avec deux chiffres après la virgule.

On n'oubliera pas de faire le zéro lorsque le pendule est à l'équilibre avant de lancer l'acquisition.

1. Fixer \(I_h = 0{,}5\,\mathrm{A}\).
2. Écarter le pendule d’un angle \(\theta_0< 45^\circ\) ; en même temps, lancer un enregistrement de \(\theta(t)\) puis lâcher le pendule.
3. \(\spadesuit\) Déterminer la pseudo-période \(T\) des oscillations (avec deux chiffres après la virgule) à l’aide du logiciel.

   Remarque : les "paramètres de mesures" que vous avez choisis pour régler l’acquisition influent sur la précision des coordonnées.

4. \(\spadesuit\) Toujours à l’aide du logiciel, mesurer deux amplitudes séparées d’une pseudo-période \(T\) puis calculer le décrément logarithmique. Recommencer cette démarche plusieurs fois avec d’autres amplitudes et en déduire sa valeur moyenne \(\Lambda\pm U_\Lambda\).
5. \(\spadesuit\) En déduire par calcul le coefficient d’amortissement \(\lambda\).
6. \(\spadesuit\) Déterminer enfin par le calcul la pulsation propre \(\omega_0\) du pendule de torsion. Aller jusqu’à trois chiffres significatifs.
7. \(\spadesuit\) Calculer la grandeur \(\dot\theta\) (voir notice) puis tracer la courbe \(\dot \theta\) en fonction de \(\theta\). Si besoin régler les paramètres d'acquisition et réenregistrer pour obtenir une courbe la plus régulière possible. Cette courbe est une trajectoire dans l'espace des phases. Interpréter cette trajectoire (pourquoi obtient-on un "escargot" ?).
8. \(\spadesuit\) Imprimer toutes les courbes, annotées et commentées.

Étude du régime critique

1. Rechercher la valeur de \(I_h\) (en observant le signal à l’écran) telle que l’on réalise le mieux possible le régime critique (voir sa définition dans la partie théorique). Si \(I_h\) dépasse 1 A, ne pas rester plus de 10 minutes avec cette valeur (l’électroaimant chauffe).
2. \(\spadesuit\) Enregistrer la courbe \(\theta(t)\).
3. \(\spadesuit\) Déterminer le coefficient d’amortissement \(\lambda\) dans ce cas (voir théorie).
4. \(\spadesuit\) En déduire une nouvelle détermination de pulsation propre du pendule. Le résultat est-il cohérent avec la partie précédente ?

Étude du régime forcé

Fixer \(I_h=0,5\,\mathrm{A}\) puis allumer le moteur du pendule. Choisir une fréquence excitatrice \(f_e\) donnant des oscillations d’amplitude ni trop forte ni trop faible (attendre que le régime transitoire disparaisse).

1. \(\spadesuit\) Mesurer \(f_e\) en utilisant un chronomètre. Par exemple, compter le temps que met la roue du moteur à effectuer 10 tours.
2. \(\spadesuit\) Enregistrer la courbe \(\theta(t)\) pendant un temps adéquat puis, avec le logiciel, calculer la grandeur \(\dot \theta\) puis tracer la courbe \(\dot\theta(t)\). Rassembler les deux courbes \(\theta(t)\) et \(\dot\theta(t)\) sur le même graphique.
3. \(\spadesuit\) À l'aide du logiciel, calculer la fréquence d'oscillation de \(\theta(t)\). Comparer avec \(f_e\).
4. \(\spadesuit\) Manipuler judicieusement l'échelle du graphique puis à l’aide du logiciel, calculer le déphasage \(\varphi\) de la vitesse angulaire \(\dot\theta(t)\) par rapport à l'angle \(\theta(t)\).

   Rappel : si l’écart temporel entre deux sinus est \(\Delta t\) alors \(\varphi=\dfrac{\Delta t}{T}\times 360\), avec \(\varphi\) exprimé en degrés.

5. \(\spadesuit\) Si l'angle s'écrit \(\theta(t)=\theta_a\cos(\omega_e t)\), comment s'écrit la vitesse angulaire \(\dot \theta(t) \) ? En déduire le déphasage théorique de \(\dot \theta\) par rapport à \(\theta\). Confronter avec votre mesure.
6. Tracer la courbe \(\dot \theta\) en fonction de \(\theta\). La comparer avec la courbe dans l'espace des phases du régime pseudo-périodique.

On veut maintenant étudier la courbe de réponse de l'oscillateur en régime forcé. Autrement dit, on cherche à connaître l'évolution de l'amplitude des oscillations \(\theta_a\) pour différentes fréquences excitatrices \(f_e\). Pour cette manipulation, on utilisera la graduation du pendule de torsion pour estimer l'amplitude crête-à-crête des oscillations \(2\theta_a\).

1. \(\spadesuit\) Calculer la fréquence propre $f_0=\dfrac{\omega_0}{2\pi}$ du pendule à partir des résultats précédents.
2. \(\spadesuit\) Relever l'amplitude crête-à-crête (lire la graduation directement sur le pendule) pour une dizaine de fréquences situées dans l'intervalle \([0-2f_0]\).
   Rappelons qu'il n'est intéressant de prendre une valeur que lorsque celle-ci change significativement de la valeiur précédente : donc ici pour une courbe de résonance, on cherche à prendre beaucoup de points au niveau du pic d'amplitude.
3. \(\spadesuit\) Rentrer ces valeurs dans Regressi™ puis tracer l'amplitude en fonction de la fréquence. Lisser la courbe.
4. \(\spadesuit\) Repérer la fréquence pour laquelle l'amplitude est maximum : c'est la fréquence de résonance \(f_r\). Théoriquement, elle est donnée par \(f_r=\sqrt{{f_0}^2-\frac{\lambda^2}{2\pi^2}}\).
   Dans cette expression, pourquoi peut-on utiliser la valeur de lambda trouvée à la 1ère manipulation (2.2) ?
   Calculer puis confronter théorie et expérience.

★★★