TP-cours : dipôle RC - CORRECTION

Correction intégrale en vidéo

Circuit et acquisition

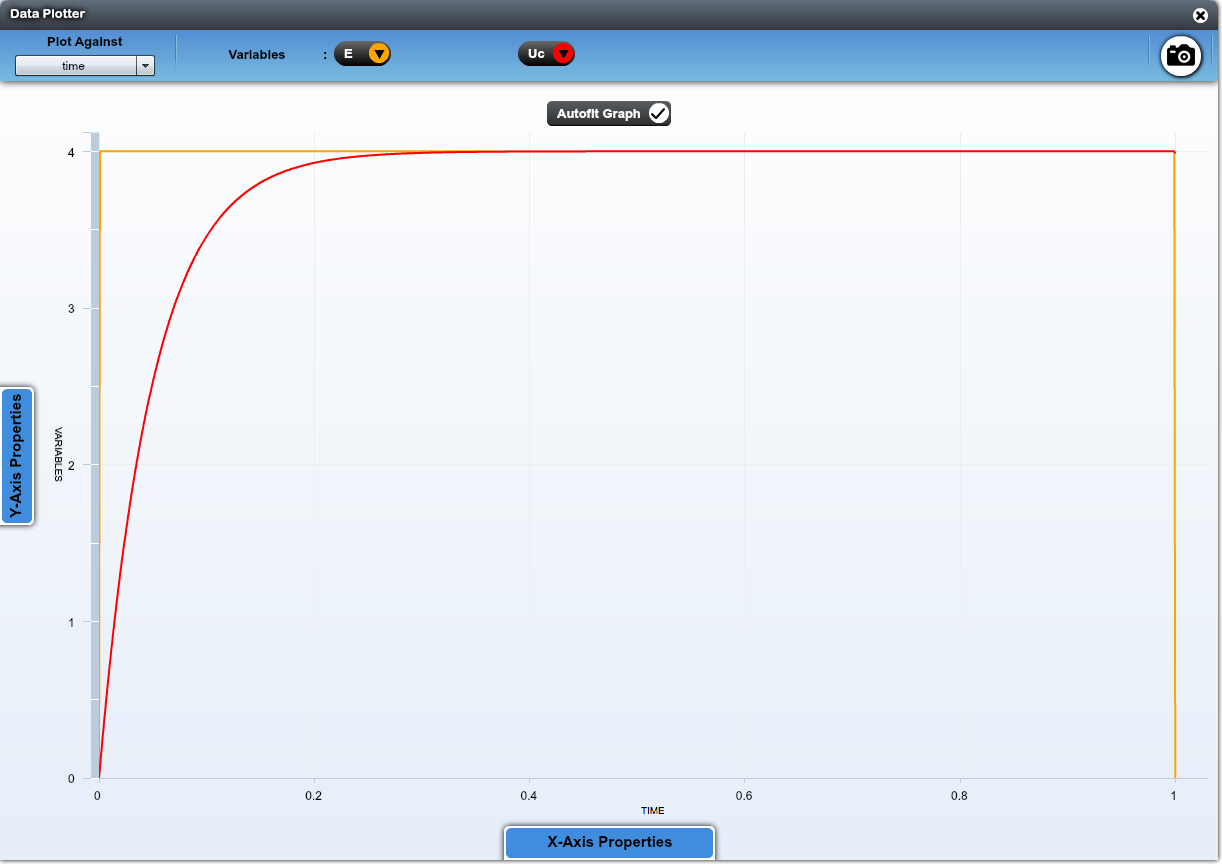
Influence de l'échelon de tension sur le phénomène

La valeur de l'échelon ne change par la variation temporelle du phénomène (on a toujours une évolution en exponentielle, avec le même $\tau$). Par contre, si l'échelon de tension fait 6V, le condensateur se chargera jusqu'à ce que la tension à ses bornes soit de 6V.

Influence de la valeurs des composants sur le régime transitoire

Plus la résistance du conducteur ohmique est grande, plus le régime transitoire est long (plus le condensateur est long à se charger). Et inversement.

De la même manière, plus la capacité du condensateur est importante, plus le régime transitoire est long. Et inversement.

Décharge du condensateur

Le condensateur étant préalablement chargé, il va se décharger dans la résistance. Le générateur est coupé. On a donc un circuit composé uniquement d'une résistance et d'un condensateur.
La loi des mailles donne : \begin{equation} u_R + u_C = 0 \Longleftrightarrow RC\,\dfrac{\mathrm{d}u_C}{\mathrm{d}t} + u_C = 0 \end{equation} La solution de cette équation différentielle est, sachant qu'à $t=0$, $u_C = E$ : \begin{equation} u_C(t) = E\,e^{-\dfrac{t}{\tau}} \end{equation}
Cette solution a pour allure :

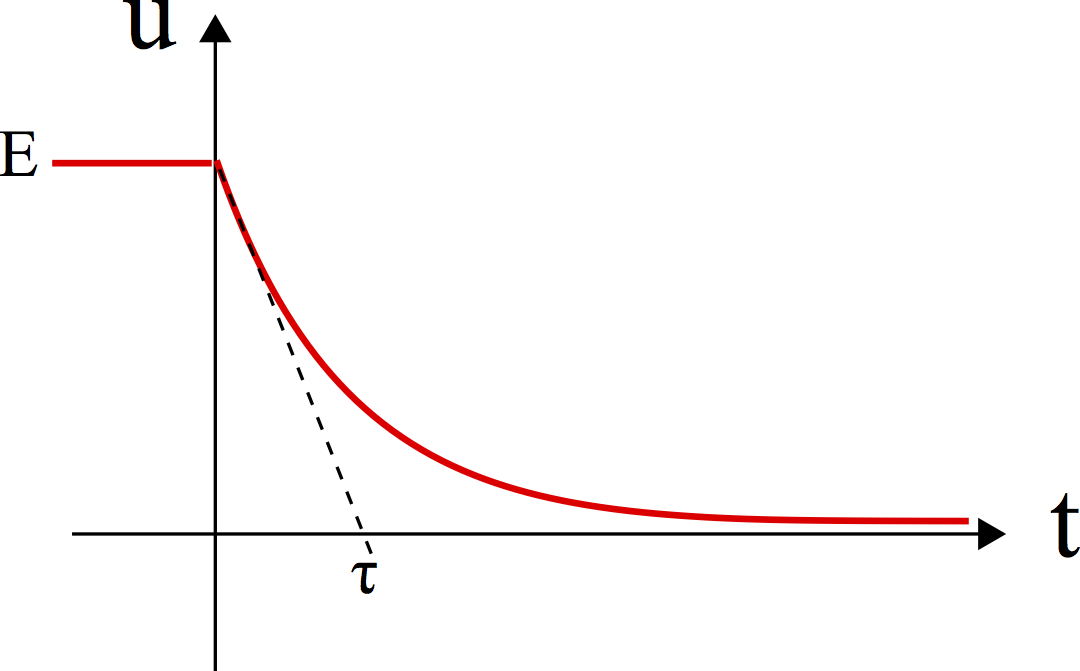
Nous voyons que pour obtenir la valeur de $\tau$, il suffit de tracer la tangente à l'origine à la courbe, celle-ci coupe l'axe des abscisses en $t = \tau$.

Simulation de la décharge

On utilise un échelon de tension de 4V à 0V qui dure 0,3 s, on règle le temps d'acquisition à 0,3 s également.

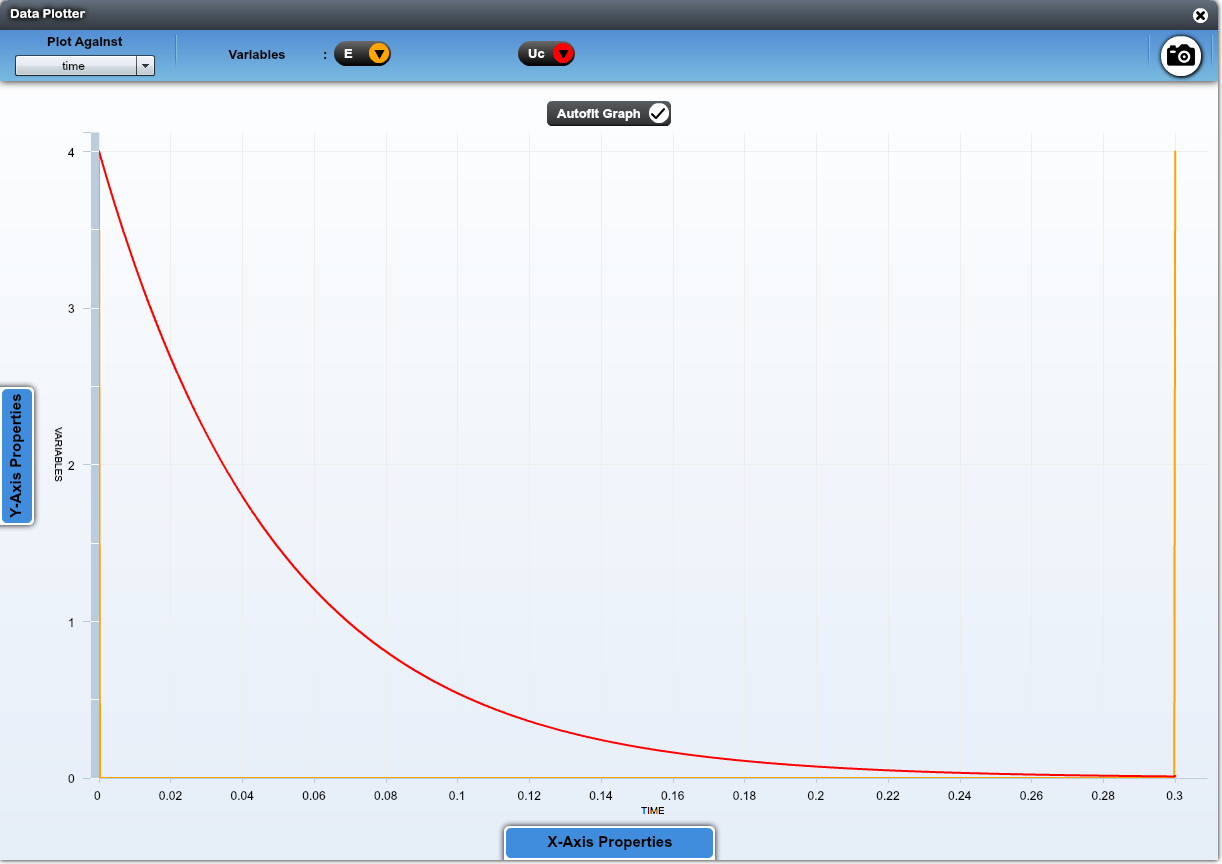
On remarque que le temps caractéristique $\tau$ est inchangé que ce soit pour la charge ou la décharge du condensateur.

La "hauteur" de l'échelon de tension ne modifie pas le comportement en exponentielle. Si on augmente $R$, le temps de décharge est plus long, si on augmente $C$, le temps de décharge est également plus long. Ceci est conforme au fait que $\tau = R \times C$.

Exercice

Première phase

1. Après avoir effectué la loi des mailles, on trouve une équation différentielle classique dont la solution est : \begin{equation} u(t) = E + (U_0 - E)\,e^{-\dfrac{t}{\tau}} \end{equation} Car le condensateur est initialement chargé sous la tension $E$.
   
   
2. On a alors deux cas :
   
   
   • Si $E \gt U_0$, le condensateur se charge (exponentiellement) de $U_0$ à $E$ ;
     
     
   • Si $E \lt U_0$, le condensateur se décharge (exponentiellement) de $U_0$ à $E$.
     
     
3. Pour obtenir l'intensité on utilise $i = C \dfrac{\mathrm{d}u}{\mathrm{d}t}$, on trouve : \begin{equation} i(t) = \dfrac{E-U_0}{R}\,e^{-\dfrac{t}{\tau}} \end{equation}
4. Perte énergétique par effet Joule :
   \begin{equation} P_\mathrm{J} = R\,i^2 \Longrightarrow E_\mathrm{J} = \dfrac{C\,(E-U_0)^2}{2} \end{equation}

Deuxième phase

5. En utilisant la loi des noeuds puis la loi des mailles, on obtient : \begin{equation} E = RC\,\dfrac{\mathrm{d}u}{\mathrm{d}t} + \left(1+ \dfrac{R}{R'}\right)\,u \end{equation}
6. En utilisant une forme canonique, on peut écrire : \begin{equation} u + \tau' \dfrac{\mathrm{d}u}{\mathrm{d}t} = \dfrac{R'}{R+R'}\,E \quad \text{avec} \quad \tau' = \dfrac{R\,R'\,C}{R+R'} \end{equation} sachant qu'à $t=0$, $u(t=0) = E$, la solution obtenue est : \begin{equation} u(t) = \dfrac{E}{R+R'}(R'+R\,e^{-\dfrac{t}{\tau'}}) \end{equation}
7. L'allure de cette fonction est :
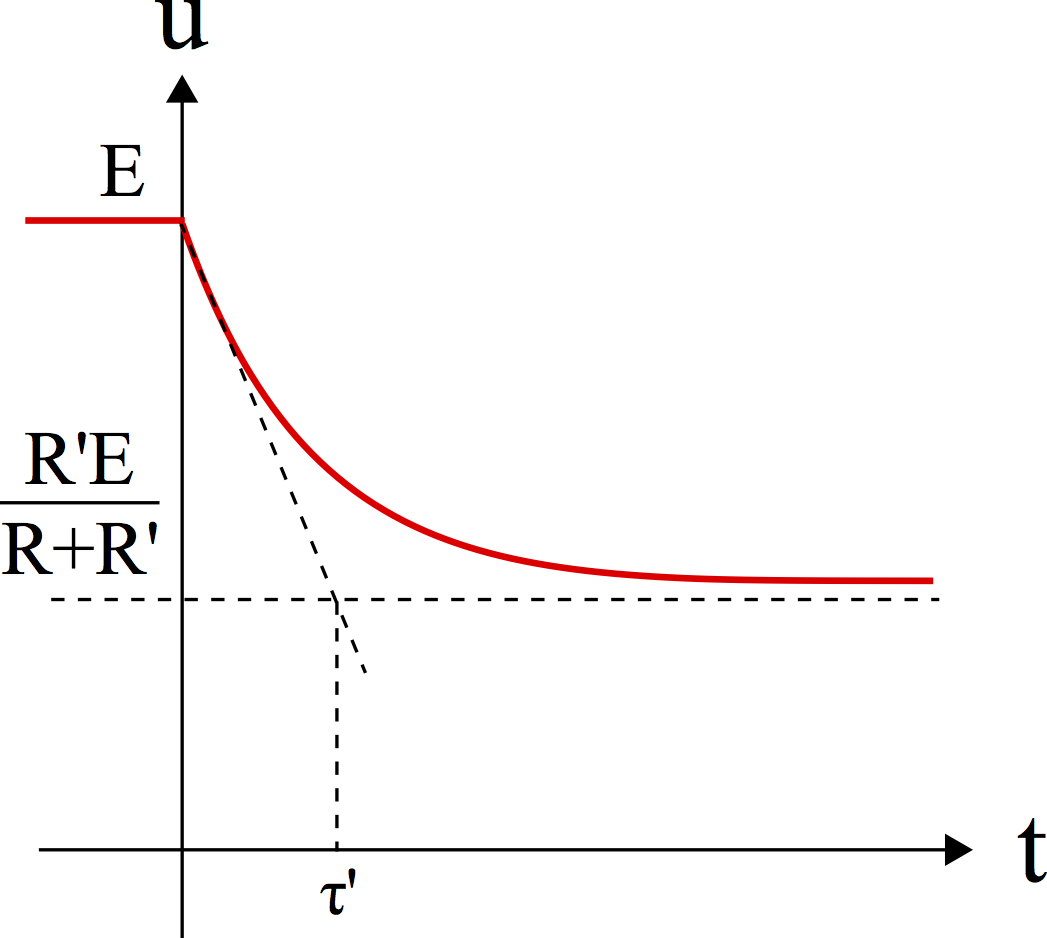   Le condensateur se décharge (exponentiellement) de $E$ à $\dfrac{R'E}{R+R'}$ en un temps caractéristique $\tau'$.