TP-cours : dipôle RC
Objectifs : découvrir le comportement du dipôle RC soumis à une échelon de tension ainsi que ses caractéristiques
Charge d'un condensateur soumis à une échelon de tension
Visionnez la vidéo ci-dessous, elle présente le condensateur et l'obtention de la tension aux bornes du condensateur lors de sa charge :
Téléchargez ici le pdf support de cette vidéo
Prise en main du logiciel de simulation
La vidéo ci-dessous vous présente l'application en ligne de simulation de circuit électrique Multisim Live.
Simulation de la charge du condensateur
Acquisition
Utilisez le logiciel de simulation pour simuler le comportement d'un dipôle RC ($R=500\,\Omega$, $C=100\,\mu F$) soumis à un échelon de tension de 4V.
Vous devez régler le temps d'acquisition ainsi que le temps que dure l'échelon de tension (ils sont confondus ici). Ce réglage se fait en fonction de la constante de temps $\tau$ du dipôle RC, on connaît le temps nécessaire pour parvenir au régime permanent.
On réglera le simulateur afin d'obtenir les courbes $u_e=f(t)$ et $u_s=f(t)$ où $u_e$ est la tension aux bornes du générateur et $u_s$ la tension aux bornes du condensateur.
Influence de l'échelon de tension sur le phénomène
Modifiez les caractéristiques de l'échelon de tension (valeur de la tension, durée de l'échelon) et observez la charge du condensateur. Notez vos observations.
Influence de la valeurs des composants sur le régime transitoire
- Simulez l'influence de la valeur du conducteur ohmique sur la charge du condensateur. Décrivez cette évolution.
- Simulez l'influence de la valeur de la capacité du condensateur sur sa charge. Décrivez cette évolution.
Traitement théorique de la décharge du condensateur
Effectuez le même travail théorique que celui présenté dans la première vidéo pour considérer cette fois-ci le cas de la décharge du condensateur (préalablement chargé sous la tension $E$) dans le conducteur ohmique : dans ce cas, on imagine le dipôle RC soumis à un échelon de tension ayant les caractéristiques suivantes :
- À $t < 0,\; u_g = E$ ;
- À $t > 0,\; u_g = 0$ .
- Donnez l'expression de la tension aux bornes du condensateur en fonction du temps.
- Représentez-la.
- Expliquez comment trouver la valeur de la constante de temps $\tau$ avec cette courbe.
Simulation de la décharge du condensateur
Utilisez le simulateur afin de modéliser la décharge du condensateur dans le conducteur ohmique.
Etudiez l'influence de l'échelon de tension, de la valeur des composants conducteur ohmique et condensateur sur le phénomène.
Exercice : condensateur préalablement chargé
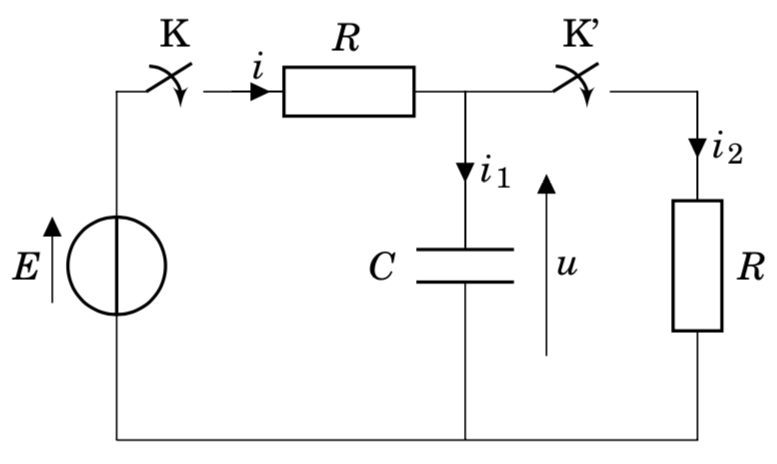
Soit le circuit représenté ci-contre.
Dans un premier temps, on étudie la charge du condensateur sous la tension $E$ : les interrupteurs K et K' étant ouvert, à l'instant $t=0$ on ferme uniquement l'interrupteur K.
Le condensateur n'est pas initialement déchargé : à $t=0$, on a $u(t=0) = U_0$.
Dans la simulation, on peut utiliser des "time delay switch", c'est à dire des interrupteurs dont la fermeture et l'ouverture sont commandés en temps.
- Exprimer la tension $u(t)$ aux bornes du condensateur en fonction des données de l'énoncé.
- Donner l'allure de cette tension dans deux cas distincts (à expliciter) et la signification de chaque allure : vérifier vos résultats par simulation, vous pouvez considérer un cas où $E=5V$ et $U_0=8V$, un autre où $E=5V$ et $U_0=2V$.
- Déterminer l'expression de l'intensité du courant lors de cette phase (fermeture de K). Dessiner l'allure mathématique de $i(t)$. Ajouter un ampèremètre dans le circuit de la simulation puis lancer celle-ci pour confirmer votre allure.
- En déduire, lors de cette même phase, la perte énergétique par effet Joule dans la résistance $R$ (intégrer la puissance Joule entre $t=0$ et $t\rightarrow\infty$).
Tout en laissant l'interrupteur K fermé, on ferme maintenant l'interrupteur K' en réinitialisant le temps à $t=0$.
- Exprimer l'intensité $i$ à l'aide de la loi des nœuds. L'injecter dans la loi des mailles relative à la maille de gauche contenant le générateur, la résistance R et le condensateur.
- En déduire l'expression de la tension aux bornes du condensateur lors de cette phase.
Indice : faire apparaître une constante de temps $\tau'$ en mettant l'équation différentielle sous sa forme canonique : $\tau' \dfrac{du}{dt}+u = \mathrm{cste} $.
- Dessiner l'allure de cette tension.


