TP-cours : dipôle RL - CORRECTION
Correction en vidéo
Circuit et acquisition
Exploitation
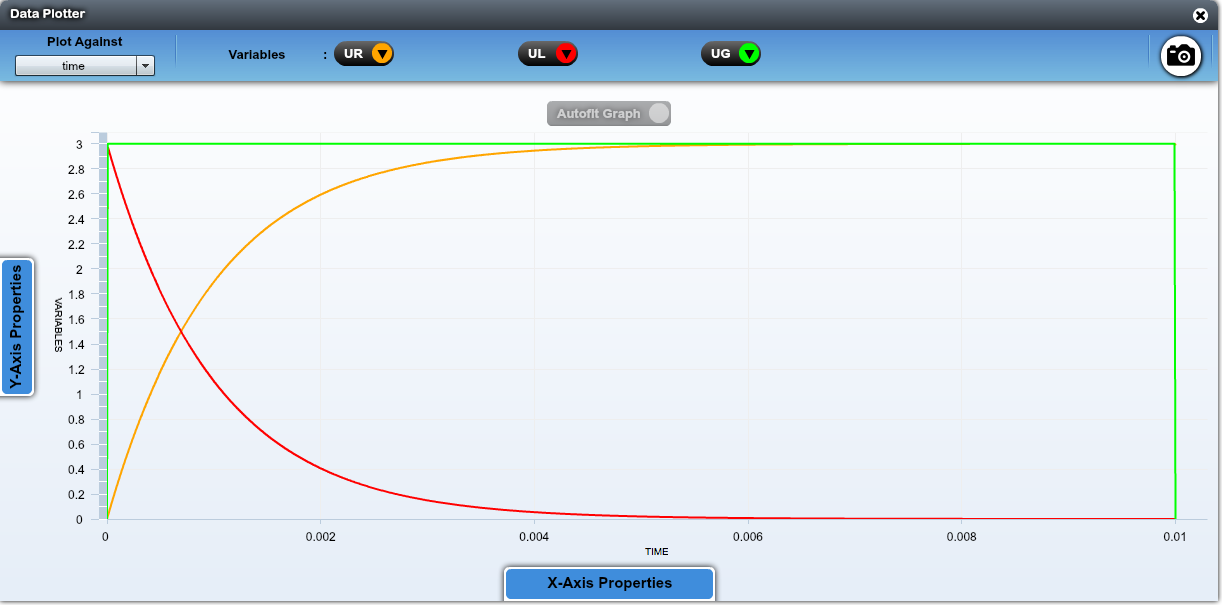
A la fin du régime transitoire, l'intensité du courant est constante.
La tension aux bornes de la bobine est nulle.
En effet, la formule qui donne la relation tension intensité dans une bobine est :
\begin{equation}
u_L = L\,\dfrac{\mathrm{d}i}{\mathrm{d}t}
\end{equation}
Donc si l'intensité du courant ne varie pas, la tension aux bornes de la bobine est nulle.
L'intensité du courant vaut théoriquement $ i = \dfrac{u_R}{R} = \dfrac{3}{100} = 0,03\,\mathrm{A}$. C'est bien ce que l'on observe à l'issue de la simulation.
On cherche l'abscisse correspondant à une ordonnée de $63\% \times E \Longleftrightarrow 0.63 \times 3 = 1.89\,\mathrm{V}$. On trouve un temps de $1 \times 10^{-3}\,\mathrm{s}$. Ceci correspond à la valeur de $\tau = \dfrac{L}{R}$.
Pour $3\tau$, on trouve une intensité de $\dfrac{2.85}{100} = 0.0285\,\mathrm{A}$ soit $95\%$ de la valeur finale.
Pour $5\tau$, on trouve une intensité de $\dfrac{2.85}{100} = 0.0298\,\mathrm{A}$ soit $99\%$ de la valeur finale : le régime permanent est établi au bout de $5\tau$.
Chute de courant
On modifie le circuit pour visualiser une chute de tension, par exemple, on réalise un échelon de tension qui passe de 3V à 0V.
On se rend compte que le temps caractéristique de cette chute, $\tau$, est le même que celui de l'établissement du courant.
Application : réalisation d'une tension triangulaire
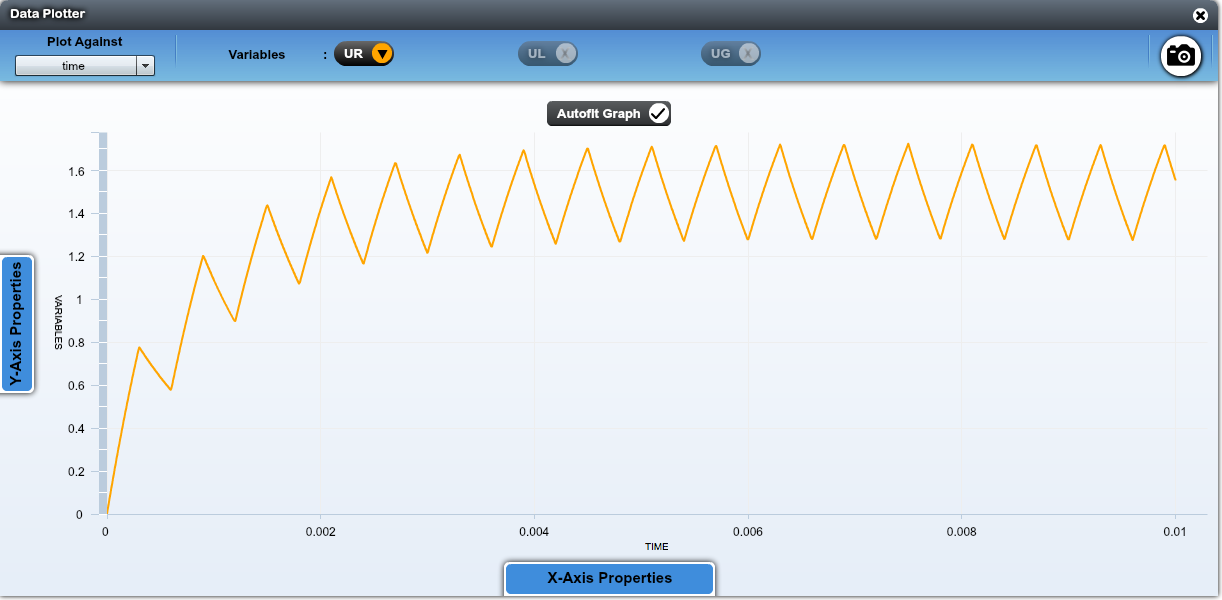
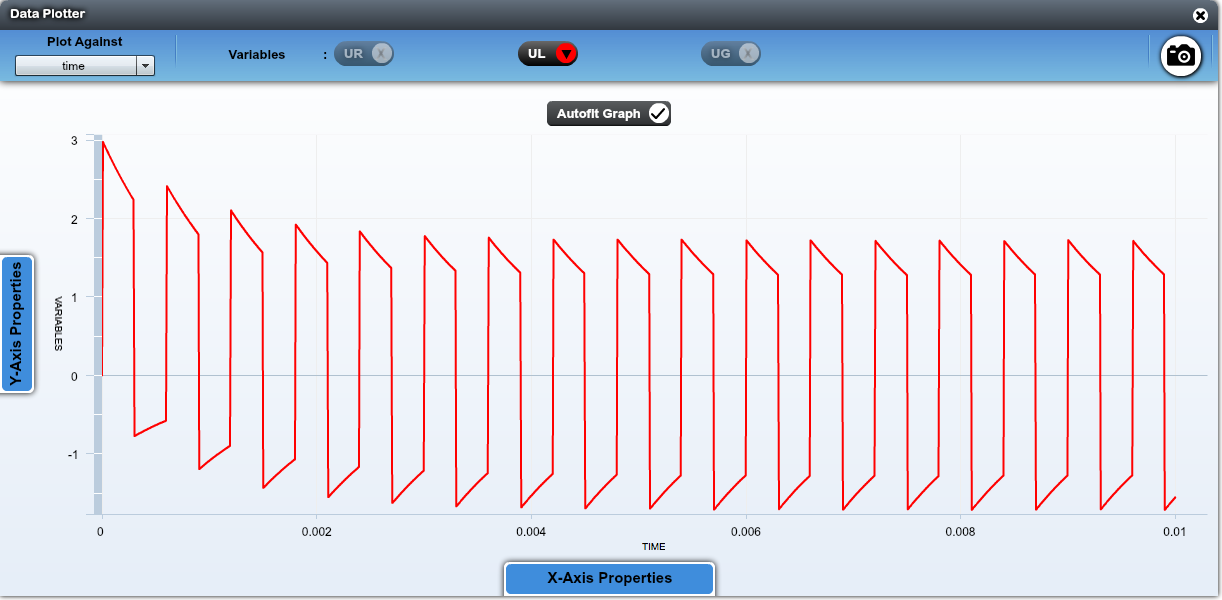
La durée du créneau est courte devant le temps caractéristique de l'établissement du courant dans le circuit. Ainsi on obtient, sur un échelon de tension de 0 à 3 V, que le début de la courbe en exponentielle obtenue au début de ce TP-cours.
Ce début est assimilable à une droite, on obtient donc une succession de droite croissante (quand le générateur passe de 0 à 3 V) et de droite décroissante (générateur passant de 3 à 0 V).
Le régime transitoire passé, la tension est pratiquement triangulaire.
On mesure une tension crête-à-crête : \(V_\text{pp}=0{,}487\,\mathrm{V}\).
Théoriquement, il suffit d'exprimer la pente du signal triangulaire en fonction de \(V_\text{pp}\) et \(T\) : \[\frac{A}{2\tau}=\frac{\Delta Y}{\Delta X}=\frac{V_\text{pp}}{T/2} \quad\text{soit}\quad V_\text{pp}=\frac{AT}{4\tau} \] Numériquement, on trouve \(V_\text{pp}=0{,}5\,V\).
La valeur est légèrement différente de la valeur expérimentale, car notre raisonnement suppose le signal parfaitement triangulaire. Or si la période est trop grande, on ne peut pas approcher les exponentielles par des droites. Ici le choix \(T=2\tau/3\) est un peu juste.


