TP : calorimétrie

Quelques aspects théoriques

Généralités

La calorimétrie repose sur les lois de la thermodynamique et permet de mesurer des capacités thermiques, des chaleurs latentes et des chaleurs de réaction.
Ce qu'il faut savoir pour ce TP :

• En calorimétrie, les transformations se font à pression constante (elles sont isobares). Dans ce cas, le transfert thermique (ou chaleur) que reçoit un liquide ou un solide lorsque sa température varie \(T_{\text{i}}\) à \(T_{\text{f}}\), s'écrit \[ Q_P=\int_{T_{\text{i}}}^{T_{\text{f}}} nc_{\text{pm}}(T)\,\mathrm{d}T \] où \(n\) désigne le nombre de mole, \(c_{\text{pm}}\) la capacité thermique molaire (J.K^-1.mol^-1) et \(T\) la température en kelvin (K).
• Dans le domaine des températures explorées, on peut considérer les capacités thermiques constantes. On aura donc \begin{equation} \boxed{\displaystyle Q_P=nc_{\text{pm}}(T_{\text{f}}-T_{\text{i}}) } \label{eq:chaleur_recue} \end{equation}
• Il existe d’autres capacités thermiques :
  • La capacité thermique massique \(c_p\) exprimée en joule par kelvin par kilogramme (J.K^-1.kg^-1) ;
  • La capacité thermique (tout court) : \(C_p = m\,c_p = n\,c_{pm}\) en joule par kelvin (J.K^-1).

  Par la suite on omettra les indices et on ne parlera que de capacité thermique massique, notée \(c\).

• Il arrive que le liquide ou le solide change d'état (solidification, fusion). Ce changement d'état (ou transition de phase) s'accompagne d'un transfert thermique sans changement de température. Par exemple, pour transformer un solide en un liquide, il faut amener le solide à la température de fusion, puis lui apporter la quantité de chaleur \begin{equation} \boxed{\displaystyle Q_P=mL_{\text{f}} } \label{eq:chaleur_latente} \end{equation} où \(L_{\text{f}}\) représente la chaleur latente de fusion (en J.kg^-1). Cette grandeur dépend de la nature du corps pur.

Capacité calorifique d’un calorimètre

L’instrument utilisé pour mesurer échanges de chaleur et capacités thermiques est un calorimètre. Un calorimètre idéal est adiabatique : il n'y a pas d’échange thermique (de chaleur) entre lui et le milieu extérieur. Ainsi, dans un calorimètre idéal contenant deux systèmes, l'un ayant reçu une chaleur \(Q_1\) et l'autre ayant reçu une chaleur \(Q_2\), on aura \begin{equation} \boxed{\displaystyle Q_1+Q_2=0 } \label{eq:relation_calorimetrique} \end{equation} Dans ce TP on fera l'hypothèse que le calorimètre est parfaitement adiabatique.

Les mesures calorimétriques étant basées sur des échanges thermiques entre sous-systèmes dans le calorimètre, il faut prendre aussi en compte les échanges thermiques entre ce que contient le calorimètre et le calorimètre lui même. On introduit alors ce que l’on appelle la valeur en eau du calorimètre que l'on note \(\mu\). On considère, qu’en ce qui concerne les échanges thermiques, le calorimètre et ses accessoires sont équivalents à une masse d’eau, \(\mu\). Ainsi, lorsque la température du calorimètre passe de \(T_1\) à \(T_2\), on devra prendre en compte le fait qu'il a reçu une chaleur

\begin{equation} Q_{\text{cal}}= \mu \times c_e (T_2-T_1) \end{equation}

avec \(c_e\) la capacité thermique massique de l'eau liquide, soit 4180 J.K^-1.kg^-1 et \(\mu\) la masse équivalente en eau du calorimètre (kg).

Dispositif expérimental

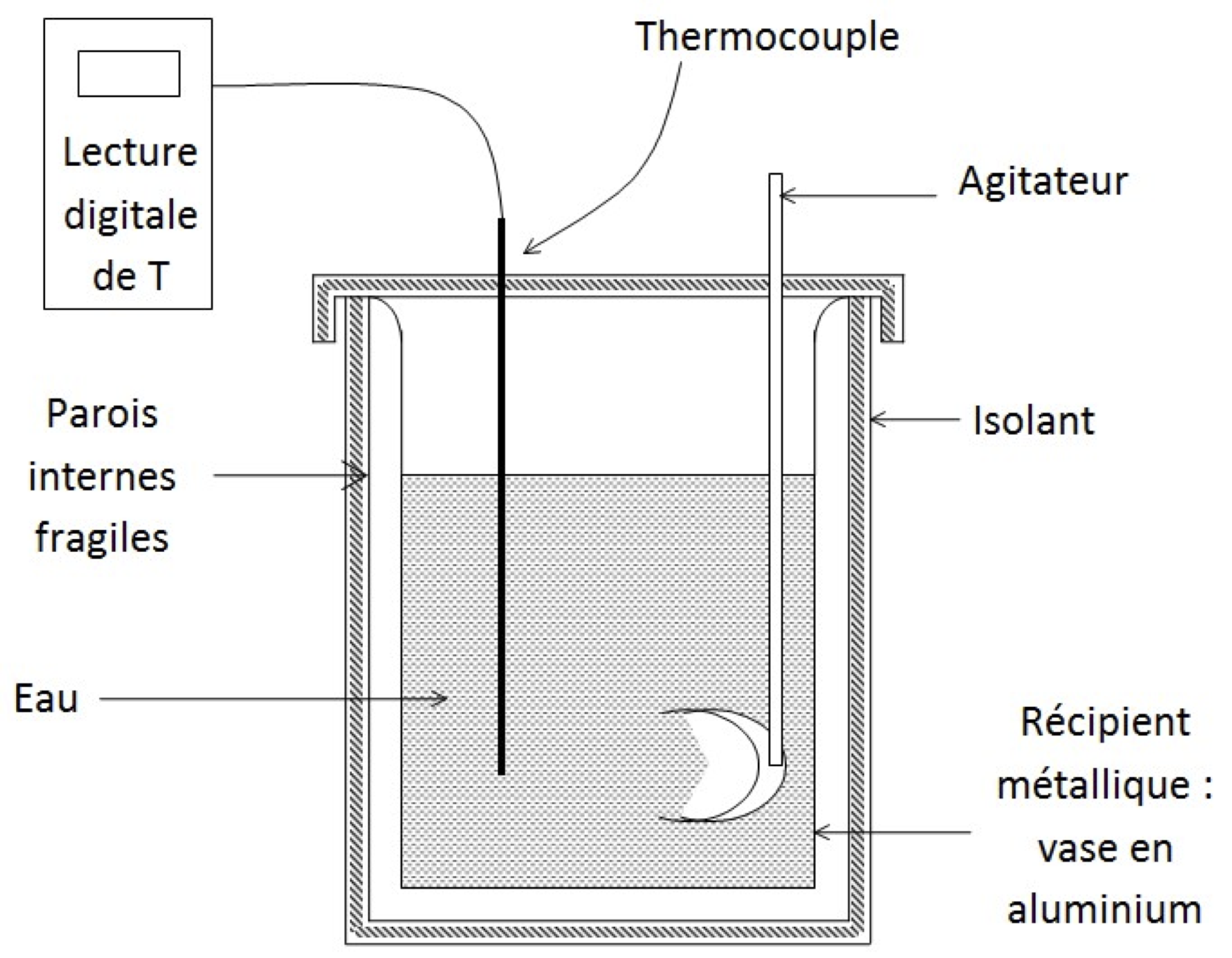
Le calorimètre est comme une "bouteille thermos", ceci afin de diminuer les pertes thermiques : l’instrument devient alors presque un calorimètre adiabatique. Il est constitué d'une paroi isolante, d'un récipient dans lequel on versera les liquides, d'un couvercle qu'on veillera à bien fermer et d'un agitateur permettant d'accélérer l'équilibre thermique.

La qualité des résultats dépendra de la façon dont vous mettrez tout en œuvre pour diminuer les pertes thermiques avec l'extérieur.

Pour chauffer les liquides, on utilise une bouilloire ou une plaque électrique. La température est relevée à l’aide d’un thermomètre à thermocouple avec lecture digitale sur un boîtier : utiliser la précision 0,1°C.

Enfin, attention aux appareils et instruments : ils sont couteux et fragiles !

Manipulation

Détermination de la capacité calorifique du calorimètre

1. Dans le calorimètre, introduire \(m'\) grammes (pas plus de \(100\,\mathrm{g}\) environ) d’eau à la température ambiante.
2. \(\spadesuit\) Noter la température d’équilibre \(T_i\).
3. \(\spadesuit\) Préparer une masse \(m\) (pas moins de \(200\,\mathrm{g}\)) d’eau tiède à une température \(T_0\) comprise entre 25°C et 40°C. Noter \(T_0\) puis verser dans le calorimètre.
   Homogénéiser le mélange en l’agitant.
4. \(\spadesuit\) Noter la nouvelle température d'équilibre \(T_f\) (elle correspond à la température minimale atteinte dans le calorimètre) et déterminer la masse totale d'eau pour connaître précisément la masse d'eau tiède versée.

5. \(\spadesuit\) Calculer \(\mu\). La détermination de \(\mu\) est importante pour la suite, c'est pourquoi, on vous demande de réaliser deux mesures de \(\mu\) (étapes 1, 2, 3 et 4).
   Comme vous êtes deux binômes sur la même manipulation, compilez vos résultats (4 mesures) et calculer une moyenne et une incertitude avec la méthode de Student.
Faire vérifier la valeur de \(\mu\) auprès de l’enseignant.

Détermination de la capacité thermique d’un métal

1. Choisir un morceau de métal et déterminer sa masse \(M\). Le porter à la température \(T_0 = 100\,^\circ \mathrm{C}\) en le mettant dans l’eau bouillante de la casserole (attendre suffisamment longtemps). Il ne faut pas que ce morceau de métal touche le fond de la casserole (qui n’est pas à \(100\,^\circ \mathrm{C}\)).
2. \(\spadesuit\) Mettre une masse \(m\) d’eau dans le calorimètre. Noter la température \(T_i\) de l’eau.
3. Immerger le morceau de métal dans l’eau du calorimètre.
   Homogénéiser en agitant.
4. \(\spadesuit\) Relever \(T_f\) à l’équilibre thermique.

5. \(\spadesuit\) Calculer \(c'\)

Détermination de la chaleur latente de fusion de la glace

1. \(\spadesuit\) Mettre une masse \(m\) d’eau chaude dans le calorimètre. Noter \(T_i\). Choisir \(T_i\) d’autant plus grande que la masse de glace sera grande.
2. Prélever une masse \(M\) de glace à la température \(T_0=0\,^\circ \mathrm{C}\).
   Important : il ne faut pas que la glace ait commencé à fondre avant son utilisation. Plonger cette glace dans le calorimètre. Homogénéiser en agitant.
3. \(\spadesuit\) Relever la température \(T_f\) à l’équilibre thermique : la glace doit être entièrement fondue et la température ne doit plus varier beaucoup.
4. \(\spadesuit\) Déterminer la masse de glace en pesant la masse totale de liquide dans le calorimètre.

5. \(\spadesuit\) Déterminer la chaleur latente de fusion de la glace \(L_F\) à partir de vos mesures

Détermination de la capacité thermique massique de l’éthanol

1. \(\spadesuit\) Prendre environ 100 cm³ d’eau et les refroidir grâce à environ 50 g de glace jusqu’à \(T_i \simeq 5\,^\circ \mathrm{C}\). Mesurer précisément la masse \(m\) d'eau. Mettre cette eau dans le calorimètre. Noter la température \(T_i\) de l’eau.
2. \(\spadesuit\) Mesurer et noter la température de l’éthanol dans sa bouteille : \(T_0\). Verser une masse \(m_0 \simeq 50\,\mathrm{g}\) (à mesurer précisément) d’éthanol dans le calorimètre.
   Homogénéiser en agitant.
3. \(\spadesuit\) Relever \(T_f\) à l’équilibre thermique.
4. \(\spadesuit\) En suivant la même démarche que dans l'expérience (3.2), déterminer la chaleur massique de l’éthanol \(c_0\).
5. \(\spadesuit\) Les tables donnent \(c_0 \simeq 2500\,\mathrm{J.kg^{-1}.K^{-1}}\). Votre mesure est-elle en accord avec les tables selon vous ? Si non, proposer une explication.
6. \(\spadesuit\) Proposer un autre protocole pour réaliser la mesure de la capacité thermique de l'éthanol et le réaliser (si le temps le permet).

★★★